Available with Geostatistical Analyst license.
Before performing moving window kriging, a geostatistical layer must be created from a kriging method other than cokriging and empirical Bayesian kriging.
The kriging parameters can be adjusted or left as the initial default values that are automatically determined by the kriging method. The rationale behind moving window kriging is to recalculate the range, nugget, and partial sill semivariogram parameters based on a smaller neighborhood.
When the data is nonstationary, you can estimate a heterogeneous semivariogram. In other words, use a moving window centered on the location to be predicted and create a semivariogram for each local neighborhood.
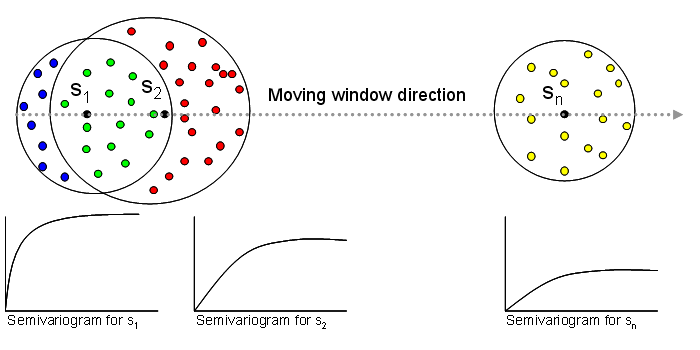
The prediction at each point in the study area can be mapped sequentially as the window moves through the study area (figure 1). In this example, the data is isotropic or invariant under rotations. To exhaustively map every location in the study area, semivariograms are calculated for each location to be predicted. Within each neighborhood, the data is assumed to be locally stationary so the assumptions of the kriging algorithm are not violated.
As the window moves through the study area, new semivariogram parameters are calculated using neighboring points. For location s1, the blue and green points are spatially correlated or within the range distance as indicated by the radius of the circle centered at that point. For location s2, the green and red points are spatially correlated, and for location sn, the yellow points are spatially correlated. This method allows you to see how the spatial structure of the data changes across the study area. If the semivariogram does not change much in different windows, this indicates that the data is close to stationary, and it is appropriate to use stationary kriging models. If, however, the semivariogram changes significantly between the moving windows, this indicates that the data is nonstationary, and it is not appropriate to use stationary kriging models.