The Local Outlier Analysis tool identifies significant clusters and outliers in your data. It finds locations in your study area that have been statistically different than their neighbors in both space and time. It takes as input a space-time NetCDF cube created using either the Create Space Time Cube By Aggregating Points tool or the Create Space Time Cube From Defined Locations tool. It then uses the Conceptualization of Spatial Relationships parameter values to calculate a space-time implementation of the Anselin Local Moran's I statistic (Cluster and Outlier Analysis) for each bin. To do this, the tool calculates a Local Moran's I index, a pseudo p-value and a type code (CO_TYPE) representing the cluster or outlier category type for each statistically significant bin in the Input Space Time Cube parameter value. The pseudo p-values represent the statistical significance of the calculated index values, and its precision is dependent on the number of permutations.
Potential applications
Applications for the Local Outlier Analysis tool can be found in many fields, including economics, resource management, political geography, demographics, public health, and fraud prevention. Some of the questions you can answer through the use of this tool include the following:
- Are there locations in my study area with anomalous spending patterns?
- Was there a time period with unexpectedly high rates of disease outbreak across the study area?
- Are there suburban areas where residents are using significantly more water than their neighbors? Or find the suburban areas that use less water consistently to develop best practices for water conservation.
- Are there any locations in my region with significant jumps in the number of insurance claims filed over the last month?
Tool outputs
A number of outputs are created by this tool. The most prominent output is a two-dimensional map summarizing each location over time added to the map upon completion of the tool. The categories are as follows:
| Type name | Definition | |
|---|---|---|
 | Never Significant | A location where there has never been a statistically significant CO_TYPE. |
 | Only High-High Cluster | A location where the only statistically significant type throughout time has been High-High Clusters. |
 | Only High-Low Outlier | A location where the only statistically significant type throughout time has been High-Low Outliers. |
 | Only Low-High Outlier | A location where the only statistically significant type throughout time has been Low-High Outliers. |
 | Only Low-Low Cluster | A location where the only statistically significant type throughout time has been Low-Low Clusters. |
 | Multiple Types | A location where there has been multiple types of statistically significant cluster and outlier types throughout time (for instance, during some time periods the location has been a Low-High Outlier, and during other time periods it has been a High-High Cluster). |
In addition, messages summarizing the analysis results are written at the bottom of the Geoprocessing pane during tool implementation.
You can access the messages by hovering over the progress bar, clicking the pop out button  , or expanding the messages section in the Geoprocessing pane. You can also access the messages for a previously run tool via the Geoprocessing History.
, or expanding the messages section in the Geoprocessing pane. You can also access the messages for a previously run tool via the Geoprocessing History.
These messages include information about the Input Space Time Cube parameter value, such as time span, temporal bias, and the number of bins and locations analyzed. The messages also include important information about any outliers that occurred in the most recent time step as well as summarizing key time steps that may be of interest. For instance, if your question involves finding underperforming areas in your sales territory and you are looking for low-high outliers, the messages will provide you with the key time step that had the highest number of low-high outliers.

This tool creates a new output feature class with the following fields summarizing the bins at each location of the Input Space Time Cube parameter value:
| Alias | Field name |
|---|---|
| Number of Outliers | NUM_OUT |
| Percentage of Outliers | PERC_OUT |
| Number of Low Clusters | N_LOW_CLS |
| Percentage of Low Clusters | P_LOW_CLS |
| Number of Low Outliers | N_LOW_OUT |
| Percentage of Low Outliers | P_LOW_OUT |
| Number of High Clusters | N_HIGH_CLS |
| Percentage of High Clusters | P_HIGH_CLS |
| Number of High Outliers | N_HIGH_OUT |
| Percentage of High Outliers | P_HIGH_OUT |
Locations with No Spatial Neighbors which are relying only on temporal neighbors for analysis calculations | NO_SP_NBR |
Locations with an Outlier in the Most Recent Time Step | OUT_R_TIME |
| Cluster Outlier Type | CO_TYPE |
Additional summary statistics including the sum, minimum value, maximum value, average, standard deviation, and median value of the variable analyzed. | SUM_VALUE, MIN_VALUE, MAX_VALUE, MEAN_VALUE, STD_VALUE, and MED_VALUE |
Finally, the Local Outlier Analysis tool adds a number of new variables to the Input Space Time Cube parameter value. If these variables already exist (if you run the Local Outlier Analysis tool for the same Analysis Variable parameter value multiple times), they will be overwritten so the cube always contains the most recent analysis results.
You can visualize these variables using ArcGIS Pro. See Visualize the space-time cube for strategies.
Interpretation
To aid in the interpretation of the Local Outlier Analysis tool results, the Make Space Time Cube Layer tool can be used to create a space-time cube layer which can display the result variables added to the cube. You can visualize the Local Moran's I Index, p-value and Cluster Outlier Analysis Type for each bin by selecting the space-time cube layer, and on the space-time cube ribbon, set the Display Theme to the appropriate theme in the Local Outlier Analysis section. An index with a positive value indicates that a bin has neighboring bins with similarly high or low attribute values; this bin is part of a cluster. An index with a negative value indicates that a bin has neighboring bins with dissimilar values; this bin is an outlier. In either instance, the pseudo p-value or p-value for the feature must be small enough for the cluster or outlier to be considered statistically significant. For more information on determining statistical significance, see What is a z-score? What is a p-value?. Note that the Local Moran's I index (I) is a relative measure and can only be interpreted within the context of its generated reference distribution and its computed pseudo p-value or p-value. The pseudo p-value or p-values reported in the output feature class are corrected for multiple testing and spatial dependency.
The cluster or outlier type distinguishes between a statistically significant cluster of high values (High-High), cluster of low values (Low-Low), outlier in which a high value is surrounded primarily by low values (High-Low), and outlier in which a low value is surrounded primarily by high values (Low-High). Statistical significance is set at the 95 percent confidence level. This significance represents an FDR correction, which adjusts the p-value threshold from 0.05 to a value that better reflects the 95 percent confidence level, taking into consideration multiple testing.
Neighborhood defaults
To determine whether the bin value at a location in space and time is part of a statistically significant hot or cold spot or a statistically significant outlier, each bin is evaluated within the context of its neighboring space-time bins. The default for this tool is to use the Fixed distance option to define relationships between bins. The parameter values for the Neighborhood Distance and Neighborhood Time Step parameters define the extent of each bin's neighborhood (the context for each bin's analysis). Suppose bin dimensions are 400 meters by 400 meters by 1 day. If you set the Neighborhood Distance parameter value to 801 meters and the Neighborhood Time Step parameter to 2, the spatial neighbors will extend two bins both horizontally and vertically, and one bin out diagonally as shown: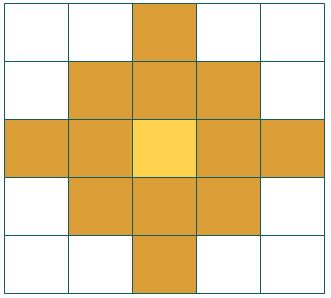
In addition, there will be temporal neighbors. All bins at the same location as the target and its spatial neighbors (shown above) for the matching or two preceding time periods—a total of three days, for this example—will be included as neighbors. Notice that temporal neighbors are backward in time only and that a Neighborhood Time Step parameter value of 2 encompasses three time-step intervals. To ensure at least 1 temporal neighbor for each location, a Local Moran's Index is not calculated for the bins in the first time slice. The bin values in the first time slice are, however, included in the calculation of the global average.
When you do not provide a value for the Neighborhood Distance parameter, a default value is calculated. The formula is adapted from the calculation used to determine a default kernel density search radius. When you do not provide a value for the Neighborhood Time Step parameter, the default value is 1.
There are additional options for defining neighborhood relationships by using the Conceptualization of Spatial Relationships parameter. For each of the options, the tool first finds spatial neighbors and then finds bins at those same locations from N previous time steps, where N is the Neighborhood Time Step parameter value you specify.
Your choice for the Conceptualization of Spatial Relationships parameter should reflect inherent relationships among the features you are analyzing. The more realistically you can model how features interact with each other in space, the more accurate your results will be. Recommendations are outlined in Best practices for selecting a conceptualization of spatial relationships.
Permutations
Permutations are used to determine how likely it would be to find the actual spatial distribution of the values that you are analyzing by comparing your values to a set of randomly generated values. Even with complete spatial randomness (CSR), some degree of clustering will always be observed simply due to randomness. Permutations will generate many random datasets and compare these values to the Local Moran's I of your original data. To do this, each permutation randomly rearranges the neighborhood values around each bin and calculates the Local Moran's I value of this random data. By looking at the distribution of the Local Moran's I generated from permutations, you can see the range of Local Moran's I values that could reasonably be due to randomness. If there is a statistically significant spatial pattern in your data, you expect the Local Moran's I values generated from permutations to display less clustering than the Local Moran's I value from your original data. A pseudo p-value is then calculated by determining the proportion of Local Moran's I values generated from permutations that display more clustering than your original data. If this proportion (the pseudo p-value) is small (less than 0.05), you can conclude that your data does display statistically significant clustering.
Choosing the number of permutations is a balance between precision and increased processing time. Increasing the number of permutations increases precision by increasing the range of possible values for the pseudo-p. For example, with 99 permutations, the precision of the pseudo-p value is .01 (1/99+1), and for 999 permutations, the precision is .001 (1/999+1). A lower number of permutations can be used when first exploring a problem, but it is best practice to increase the permutations to the highest number feasible for final results.
Additional resources
Anselin, Luc. "Local Indicators of Spatial Association—LISA," Geographical Analysis 27(2): 93–115, 1995.
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.