Available with Spatial Analyst license.
The Rescale by Function tool allows you to use a mathematical function (line or curve) to assign suitability values to an input raster along a continuous scale (typically 1 to 10). Rescaling is particularly useful in suitability modeling. Many times, the suitability changes continuously with the changing values of the criterion and often does so in a nonlinear manner. For example, cell locations close to existing roads may be the most preferred in a housing suitability model since the cost of getting power to those locations is cheaper. As the distance from a road increases, the cost of getting power to those locations may increase exponentially. As a result, the suitability for farther locations may decrease dramatically. Once the cost interaction is established, the exponential preferential decrease is transformed to a specified continuous suitability scale, for example, on a 1 to 10 scale. The scaled cost criterion can then be integrated with the other scaled criterion, such as slope, aspect, and distance from schools, to identify the best locations for houses.
There are four main considerations when applying this tool:
- Understand and define the preference interaction between the phenomenon and the criterion.
- Select the transformation function that best captures that preference interaction (for example, Exponential increase).
- Optionally modify the function parameters to obtain a better fit.
- Define an suitability (evaluation) scale to transform the preference function values (for example, 1 to 10).
The Rescale by Function tool expands your options for transforming data in a suitability model. You can use the Reclassify tool to reclassify data into categories and the Rescale by Function tool to rescale (reclassify) continuous data without creating discrete categories. The Rescale by Function tool provides a variety of functions to model suitabilities which change on a continuous scale. Since the tool rescales the input raster values onto a continuous suitability scale, there is no aggregation into categories, thus allowing you to better capture certain continuously changing preference interactions (for the example above, the cost changes as distance from the road increases).
The available functions are: Exponential, Gaussian, Large, Linear, Logarithm, Logistic Decay, Logistic Growth, MSLarge, MSSmall, Near, Power, Small, and Symmetric Linear. More details on each of the individual functions are available here:
You can define upper and lower thresholds to give you more control over how the rescaling of the input values occurs. See The interaction of the lower and upper thresholds on the output values for more details.
Essential vocabulary
The following definitions are for some commonly used terms when discussing Rescale by Function.
- Phenomenon—The item being modeled (for example, a deer, a house, a road, or a shopping center).
- Preference value—A value indicating how much the phenomenon prefers the feature at a particular location.
- Criterion—The feature to which the phenomenon is responding (for example, slope, aspect, distance from roads, or land-use type).
- Suitability value—The same as preference value, except the preference is in the context of a suitability model.
- Evaluation scale—A relative scale to place the preference or suitability values. Generally, a cell assigned a higher evaluation value contains features that are more preferred by the phenomenon relative to the criterion being analyzed. Common evaluation scales include 1 to 10, 0 to 1, and 1 to 100.
- Suitability scale—The same as the evaluation scale.
- Continuous values—The values within a raster have a relative meaning. For example, a cell 100 meters above sea level is half as high as a cell assigned 200 meters. Examples of continuous data include elevation, ozone concentration, and suitability values.
- Categorical values—The values within a raster do not have relative meaning. For example, a cell with a land-use type of 4 is not half the land use as a cell assigned a type 8. Examples of categorical data include land-use type, county names, and ZIP Codes.
- Continuous output scale—The values within a specified range continuously increase or decrease without discrete classes. Generally, continuous values are represented by floating-point values.
Transforming the data
The Rescale by Function tool rescales continuous data onto a specified suitability scale, based on a mathematical function (such as Exponential, Power, and Logarithm) that you can select. Transforming the input data is conceptually a two-step process, first a transformation function is applied, then the function values are mapped to a suitability scale (typically 1 to 10).
Applying the transformation function.
The specified function is applied to the values that fall within the lower and upper threshold values.
Rescaling the transformed data to the evaluation scale
The following graph illustrates how the function values are mapped to the evaluation scale.
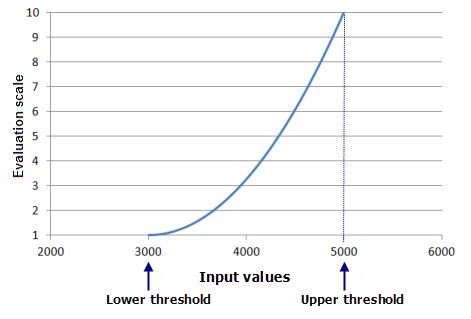
The minimum and maximum transformed function values, f(x), are rescaled to the minimum and maximum of the evaluation scale, respectively. Many of the functions are monotonic (continuously increase or decrease). As a result, the lower and upper thresholds will generally map to the minimum and maximum values on the evaluation scale, since they will be the lowest and highest f(x) values.
In the previous example, the lower and upper thresholds are equal to the minimum and maximum of the input data (3,000 and 5,000, respectively). As a result, the lowest input value is assigned a 1 on a 1 to 10 evaluation scale and the maximum input value a 10. However, this does not need to be the case. For example, if the Power function is applied to the same input data (ranging from 3,000 to 5,000), and if the lower threshold is set to 3,500 and the upper threshold to 4,500, then a cell location with an input value of 3,500 will be assigned a 1 on a 1 to 10 output evaluation scale, and the input value of 4,500 will be assigned a 10. All other values will range between the two based on their transformed value. Input values below the lower threshold and above the upper threshold will be assigned to the values you specify.
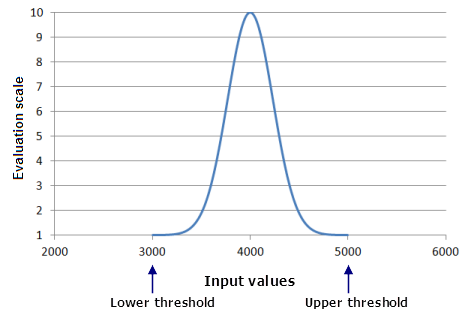
Not all functions continuously increase or decrease, however, so the lowest and highest input values may not always map to the lowest and highest evaluation values. By default, in the Gaussian function, the midpoint is the value that determines the highest point of the function (the most preferred value). This is set to the midpoint of your input data. Locations with the minimum and maximum input values will produce the lowest function values, f(x), once the Gaussian function is applied. Therefore, cells with the minimum and maximum input values will be assigned a 1 in the output raster. The midpoint value produces the highest function value, f(x). As a result, cells containing input values equal to this midpoint will be assigned a value of 10 on the output raster.
The Gaussian function might be useful in a suitability model for identifying the best habitat for a rare species of Masdevallia orchid. The orchid is sensitive to elevation. It grows best at an elevations around 4,000 meters. As the elevation increases from there, it quickly becomes too cold for the orchid; as the elevation decreases, it becomes too warm. When rescaling the elevation, the value of 4,000 meters is the most preferred, with other elevations (both higher and lower) being the least preferred.
You can assign any input value below the lower threshold or above the upper threshold to a desired output value (within or outside the evaluation scale or to NoData) using the Value below threshold and Value above threshold parameters. The transformation function will not be applied to these locations.
Defining the transformation
There are two primary approaches to consider when defining a continuous transformation:
- Accept the defaults.
The shape-controlling parameters (see description below) will be calculated to fit the function between the minimum and maximum values of the input raster. This is a data-dependent scenario since the function is fit to the data.
- Select the function which best models the suitability.
Change the shape-controlling parameters of the function to fine-tune the shape of the function to best reflect the suitability. To make the function data independent, set the lower and upper threshold to the appropriate values to fit to the phenomenon's preference to the criterion values regardless of the input data values.
The transformation function parameters
Types of function parameters
There are two types of parameters associated with each transformation function, parameters which control the:
- Shape of the function
Examples of these parameters are the Base factor, Input shift, and Midpoint. These parameters define how steep the function increases or decreases, where the function evaluation begins, and the transition points within the function.
- Mapping of the function to the suitability evaluation scale
Examples of these are the threshold parameters, such as Lower threshold and Value above threshold.
General format of the function parameters
Following is the general format of the parameters for each function and their characteristics:
- Function ({Shape Parameter 1}, {Shape Parameter 2}, {Shape Parameter 3}, {Lower threshold}, {Value below threshold}, {Upper threshold}, {Value above threshold})
For these parameters
- Each function consists of shape-controlling parameters and respective threshold parameters.
- The number of shape-controlling parameters depends on the transformation function, with most having two parameters but some having three.
- The threshold parameters are consistent across all functions.
- Default values for shape-controlling parameters are calculated using data values from the input raster.
- All parameters for the function are optional.
- The values of the Value below threshold and Value above threshold parameters can be a number (a double) or the string "NoData". All others parameters are of type double.
Example of the general format of the Exponential function
To demonstrate how the general format described above would apply to a specific transformation function, the following is what the parameters would be if the Transformation function was set to Exponential:
Exponential (Input shift, Base factor, Lower threshold, Value below threshold, Upper threshold, Value above threshold)
The Input shift and Base factor are the shape-controlling parameters. The Lower threshold, Value below threshold, Upper threshold, and Value above threshold are threshold parameters.
By default, minimum and maximum data values define the lower and upper boundaries for the function.
The interaction of the parameters within the tool dialog
For the Input raster parameter, the Lower threshold is set to the minimum value of that raster, the Upper threshold is set to the maximum value from it, and the shape-controlling parameters (for example, Input shift, Base factor, and Midpoint) are calculated automatically to best fit (constrain) the function between the Lower threshold and Upper threshold.
There is an interaction between the threshold parameters, which control the mapping of the function values to the suitability scale, with the shape-controlling parameters that define the function curve. For example, once the defaults are determined, you can type in a larger value for the Upper threshold. The associated shape-controlling parameters will be recalculated and updated in the dialog (for example, the Input shift and Base factor). However, if you type in a new value for one of the shape-controlling parameters (for example, a new Base factor), the relationship to the associated threshold parameters controlling the mapping to the suitability scale is severed, and you are then in control. Using the Exponential function as an example, if you type in a new Base factor and change the Upper threshold, a new Base factor will not be automatically recalculated. The tool will use the Base factor you specified. For another example, this time using the Linear function, by default the Upper threshold is set to the maximum of Input raster. If you enter a larger value for the Upper threshold, the Maximum parameter for the Linear function will be automatically updated. However, if you type in a new Maximum value and change the Upper threshold, the Maximum will not change.
Through this dialog interaction, the function by default is fit between the Lower threshold and Upper threshold, which are initially set to the minimum and maximum of the Input raster. However, you can have full control over the shape of the function and the mapping to the evaluation scale by entering your own values.
If you change a function parameter and want it to return to its default value, you can select and delete the value, then click in another parameter field, which will cause the empty parameter to be recalculated back to the default value. For example, if you entered a value for the Base factor but want to return to having the function fit between the Lower threshold and Upper threshold, delete the Base factor parameter value, click in another parameter field, and a new Base factor is calculated that fits the function between the thresholds.
Note:
The MSSmall and MSLarge functions do not follow this interaction behavior because the two functions are dependent upon the mean and standard deviation of the input dataset.