| Label | Explanation | Data Type |
Input Features | The point or polygon feature class for which the cluster and outlier analysis will be performed. | Feature Layer |
Output Features
| The output feature class to receive the result fields. | Feature Class |
Analysis Field
(Optional) | The numeric field (number of incidents, crime rates, test scores, and so on) to be evaluated. | Field |
Incident Data Aggregation Method
(Optional) | The aggregation method to use to create weighted features for analysis from incident point data.
| String |
Bounding Polygons Defining Where Incidents Are Possible
(Optional) | A polygon feature class defining where the incident Input Features could possibly occur. | Feature Layer |
Polygons For Aggregating Incidents Into Counts
(Optional) | The polygons to use to aggregate the incident Input Features in order to get an incident count for each polygon feature. | Feature Layer |
Performance Adjustment
(Optional) | This analysis utilizes permutations to create a reference distribution. Choosing the number of permutations is a balance between precision and increased processing time. Choose your preference for speed versus precision. More robust and precise results take longer to calculate.
| String |
Cell Size
(Optional) | The size of the grid cells used to aggregate the Input Features. When aggregating into a hexagon grid, this distance is used as the height to construct the hexagon polygons. | Linear Unit |
Distance Band
(Optional) | The spatial extent of the analysis neighborhood. This value determines which features are analyzed together in order to assess local clustering. | Linear Unit |
Summary
Given incident points or weighted features (points or polygons), creates a map of statistically significant hot spots, cold spots, and spatial outliers using the Anselin Local Moran's I statistic. It evaluates the characteristics of the input feature class to produce optimal results.
Illustration
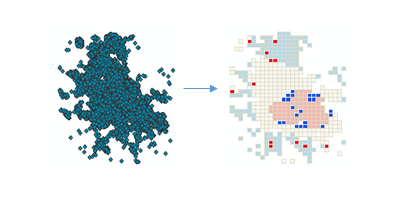
Usage
This tool identifies statistically significant spatial clusters of high values (hot spots) and low values (cold spots) as well as high and low outliers within your dataset. It automatically aggregates incident data, identifies an appropriate scale of analysis, and corrects for both multiple testing and spatial dependence. This tool interrogates your data in order to determine settings that will produce optimal cluster and outlier analysis results. If you want full control over these settings, use the Cluster and Outlier Analysis tool instead.
Note:
Incident data are points representing events (crime, traffic accidents) or objects (trees, stores) where your focus is on presence or absence rather than a measured attribute associated with each point.
The computed settings used to produce optimal cluster and outlier analysis results are reported as messages during tool execution. The associated workflows and algorithms are explained in How Optimized Outlier Analysis works.
This tool creates a new Output Feature Class with a Local Moran's I index (LMiIndex), z-score, pseudo p-value and cluster/outlier type (COType) for each feature in the Input Feature Class. It also includes a field (NNeighbors) with the number of neighbors each feature included in its calculations.
The output of this tool includes a histogram charting the value of the variable analyzed (either the Analysis Field or the incident count within each polygon). The chart can be accessed under the output feature class on the Contents pane.
The COType field identifies statistically significant high and low clusters (HH and LL) as well as high and low outliers (HL and LH), corrected for multiple testing and spatial dependence using the False Discovery Rate (FDR) correction method.
The z-scores and p-values are measures of statistical significance that tell you whether or not to reject the null hypothesis, feature by feature. In effect, they indicate whether the apparent similarity (a spatial clustering of either high or low values) or dissimilarity (a spatial outlier) is more pronounced than one would expect in a random distribution. The z-score and p-values in the Output Feature Class do not reflect any kind of FDR (False Discovery Rate) corrections. For more information on z-scores and p-values, see What is a z-score? What is a p-value?
A high positive z-score for a feature indicates that the surrounding features have similar values (either high values or low values). The COType field in the Output Feature Class will be HH for a statistically significant cluster of high values and LL for a statistically significant cluster of low values.
A low negative z-score (for example, less than -3.96) for a feature indicates a statistically significant spatial data outlier. The COType field in the Output Feature Class will indicate if the feature has a high value and is surrounded by features with low values (HL) or if the feature has a low value and is surrounded by features with high values (LH).
The COType field will always indicate statistically significant clusters and outliers based on a False Discovery Rate corrected 95 percent confidence level. Only statistically significant features have values for the COType field.
When the Input Feature Class is not projected (that is, when coordinates are given in degrees, minutes, and seconds) or when the output coordinate system is set to a Geographic Coordinate System, distances are computed using chordal measurements. Chordal distance measurements are used because they can be computed quickly and provide very good estimates of true geodesic distances, at least for points within about thirty degrees of each other. Chordal distances are based on an oblate spheroid. Given any two points on the earth's surface, the chordal distance between them is the length of a line, passing through the three-dimensional earth, to connect those two points. Chordal distances are reported in meters.
Caution:
Be sure to project your data if your study area extends beyond 30 degrees. Chordal distances are not a good estimate of geodesic distances beyond 30 degrees.
The Input Features can be points or polygons. With polygons, an Analysis Field is required.
If you provide an Analysis Field, it should contain a variety of values. The math for this statistic requires some variation in the variable being analyzed; for example, it cannot solve if all input values are 1.
With an Analysis Field, this tool is appropriate for all data (points or polygons) including sampled data. In fact, this tool is effective and reliable even in cases where there is oversampling. With lots of features (oversampling), the tool has more information to compute accurate and reliable results. With few features (undersampling), the tool will still do all it can to produce accurate and reliable results, but there will be less information to work with.
With point data you will sometimes be interested in analyzing data values associated with each point feature and will consequently provide an Analysis Field. In other cases, you will only be interested in evaluating the spatial pattern (clustering) of the point locations or point incidents. The decision to provide an Analysis Field or not will depend on the question you are asking.
- Analyzing point features with an Analysis Field allows you to answer questions such as Where do high and low values cluster?
- The analysis field you select might represent the following:
- Counts (such as the number of traffic accidents at street intersections)
- Rates (such as city unemployment, where each city is represented by a point feature)
- Averages (such as the mean math test score among schools)
- Indices (such as a consumer satisfaction score for car dealerships across the country)
- Analyzing point features when there is no Analysis Field allows you to identify where point clustering is unusually (statistically significant) intense or sparse. This type of analysis answers questions such as Where are there many points? Where are there very few points?
When you don't provide an Analysis Field the tool will aggregate your points in order to obtain point counts to use as an analysis field. There are three possible aggregation schemes:
- For Count incidents within fishnet grid and Count incidents within hexagon grid, an appropriate polygon cell size is computed and used to create a fishnet or hexagon polygon mesh which is then positioned over the incident points and the points within each polygon cell are counted. If no Bounding Polygons Defining Where Incidents Are Possible feature layer is provided, the cells with zero points are removed and only the remaining cells are analyzed. When a bounding polygon feature layer is provided, all cells that fall within the bounding polygons are retained and analyzed. The point counts for each polygon cell are used as the analysis field.
Note:
Although fishnet grids are the more common aggregation shape used, hexagons may be a better option for certain analyses.
- For Count incidents within aggregation polygons, you need to provide the Polygons For Aggregating Incidents Into Counts feature layer. The point incidents falling within each polygon will be counted and these polygons with their associated counts will then be analyzed. The Count incidents within aggregation polygons option is an appropriate aggregation strategy when points are associated with administrative units such as tracts, counties, or school districts. You might also use this option if you want the study area to remain fixed across multiple analyses to enhance making comparisons.
- For Snap nearby incidents to create weighted points, a snap distance is computed and used to aggregate nearby incident points. Each aggregated point is given a count reflecting the number of incidents that were snapped together. The aggregated points are then analyzed with the incident counts serving as the analysis field. The Snap nearby incidents to create weighted points option is an appropriate aggregation strategy when you have many coincident, or nearly coincident, points and want to maintain aspects of the spatial pattern of the original point data.
Note:
In many cases you will want to try Snap nearby incidents to create weighted points, Count incidents within fishnet grid and Count incidents within hexagon grid to see which result best reflects the spatial pattern of the original point data. Fishnet and hexagon solutions can artificially separate clusters of point incidents, but the output may be easier for some people to interpret than weighted point output. Although fishnet grids tend to be the most common aggregation shape used, hexagons may be a better option for certain analyses.Caution:
Analysis of point data without specifying an Analysis Field only makes sense when you have all of the known point incidents and you can be confident there is no bias in the point distribution you are analyzing. With sampled data you will almost always be including an Analysis Field (unless you are specifically interested in the spatial pattern of your sampling scheme).
- For Count incidents within fishnet grid and Count incidents within hexagon grid, an appropriate polygon cell size is computed and used to create a fishnet or hexagon polygon mesh which is then positioned over the incident points and the points within each polygon cell are counted. If no Bounding Polygons Defining Where Incidents Are Possible feature layer is provided, the cells with zero points are removed and only the remaining cells are analyzed. When a bounding polygon feature layer is provided, all cells that fall within the bounding polygons are retained and analyzed. The point counts for each polygon cell are used as the analysis field.
When you select Count incidents within fishnet grid or Count incidents within hexagon grid for the Incident Data Aggregation Method, you may optionally provide a Bounding Polygons Defining Where Incidents Are Possible feature layer. When no bounding polygons are provided, the tool cannot know if a location without an incident should be a zero to indicate that an incident is possible at that location, but didn't occur, or if the location should be removed from the analysis because incidents would never occur at that location. Consequently, when no bounding polygons are provided, only cells with at least one incident are retained for analysis. If this isn't the behavior you want, you can provide a Bounding Polygons Defining Where Incidents Are Possible feature layer to ensure that all locations within the bounding polygons are retained. Fishnet or hexagon cells with no underlying incidents will receive an incident count of zero.
Any incidents falling outside the Bounding Polygons Defining Where Incidents Are Possible or the Polygons For Aggregating Incidents Into Counts will be excluded from analysis.
The Performance Adjustment parameter specifies how many permutations are used in the analysis. Choosing the number of permutations is a balance between precision and increased processing time. Increasing the number of permutations increases precision by increasing the range of possible values for the pseudo-p.
Permutations are used to determine how likely it would be to find the actual spatial distribution of the values you are analyzing. For each permutation, the neighborhood values around each feature are randomly rearranged and the Local Moran's I value calculated. The result is a reference distribution of values that is then compared to the actual observed Moran's I to determine the probability that the observed value could be found in the random distribution. The default is 499 permutations; however, the random sample distribution is improved with increasing permutations, which improves the precision of the pseudo p-value.
The tool will calculate the optimal scale of analysis based on the characteristics of your data or you may set the scale of analysis through the Distance Band parameter in the Override Settings. For features with no neighbors at this distance, the Distance Band is extended so each feature has at least one neighbor.
Instead of letting the tool choose optimal defaults for grid cell size and scale of analysis, the Override Settings can be used to set the Cell Size or Distance Band for the analysis.
The Cell Size option allows you to set the size of the grid used to aggregate your point data. You may decide to make each cell in the fishnet grid 50 meters by 50 meters, for example. If you are aggregating into hexagons, the Cell Size is the height of each hexagon and the width of the resulting hexagons will be 2 times the height divided by the square root of 3.

You should use the Space Time Pattern Mining tools or the Generate Spatial Weights Matrix and Cluster and Outlier Analysis tools if you want to identify space-time hot spots. More information about space-time cluster analysis is provided in the Space Time Pattern Mining documentation or the Space-Time Cluster Analysis topic.
-
Map layers can be used to define the Input Feature Class. When using a layer with a selection, only the selected features are included in the analysis.
The Output Features layer is automatically added to the table of contents with default rendering applied to the COType field. The rendering is defined by a layer file in <ArcGIS Pro>\Resources\ArcToolBox\Templates\Layers. You can reapply the default rendering, if needed, by using the Apply Symbology From Layer tool.
Caution:
When using shapefiles, keep in mind that they cannot store null values. Tools or other procedures that create shapefiles from nonshapefile inputs may store or interpret null values as zero. In some cases, nulls are stored as very large negative values in shapefiles. This can lead to unexpected results. See Geoprocessing considerations for shapefile output for more information.
Parameters
arcpy.stats.OptimizedOutlierAnalysis(Input_Features, Output_Features, {Analysis_Field}, {Incident_Data_Aggregation_Method}, {Bounding_Polygons_Defining_Where_Incidents_Are_Possible}, {Polygons_For_Aggregating_Incidents_Into_Counts}, {Performance_Adjustment}, {Cell_Size}, {Distance_Band})| Name | Explanation | Data Type |
Input_Features | The point or polygon feature class for which the cluster and outlier analysis will be performed. | Feature Layer |
Output_Features | The output feature class to receive the result fields. | Feature Class |
Analysis_Field (Optional) | The numeric field (number of incidents, crime rates, test scores, and so on) to be evaluated. | Field |
Incident_Data_Aggregation_Method (Optional) | The aggregation method to use to create weighted features for analysis from incident point data.
| String |
Bounding_Polygons_Defining_Where_Incidents_Are_Possible (Optional) | A polygon feature class defining where the incident Input_Features could possibly occur. | Feature Layer |
Polygons_For_Aggregating_Incidents_Into_Counts (Optional) | The polygons to use to aggregate the incident Input_Features in order to get an incident count for each polygon feature. | Feature Layer |
Performance_Adjustment (Optional) | This analysis utilizes permutations to create a reference distribution. Choosing the number of permutations is a balance between precision and increased processing time. Choose your preference for speed versus precision. More robust and precise results take longer to calculate.
| String |
Cell_Size (Optional) | The size of the grid cells used to aggregate the Input_Features. When aggregating into a hexagon grid, this distance is used as the height to construct the hexagon polygons. | Linear Unit |
Distance_Band (Optional) | The spatial extent of the analysis neighborhood. This value determines which features are analyzed together in order to assess local clustering. | Linear Unit |
Code sample
The following Python window script demonstrates how to use the OptimizedOutlierAnalysis function.
import arcpy
arcpy.env.workspace = r"C:\OOA"
arcpy.stats.OptimizedOutlierAnalysis("911Count.shp", "911OptimizedOutlier.shp",
"#", "SNAP_NEARBY_INCIDENTS_TO_CREATE_WEIGHTED_POINTS",
"#", "#", "BALANCED_499")The following stand-alone Python script demonstrates how to use the OptimizedOutlierAnalysis function.
# Analyze the spatial distribution of 911 calls in a metropolitan area
# Import system modules
import arcpy
# Set property to overwrite existing output, by default
arcpy.env.overwriteOutput = True
# Local variables...
workspace = r"C:\OOA\data.gdb"
try:
# Set the current workspace (to avoid having to specify the full path to
# the feature classes each time)
arcpy.env.workspace = workspace
# Create a polygon that defines where incidents are possible
# Process: Minimum Bounding Geometry of 911 call data
arcpy.management.MinimumBoundingGeometry("Calls911", "Calls911_MBG",
"CONVEX_HULL", "ALL", "#",
"NO_MBG_FIELDS")
# Optimized Outlier Analysis of 911 call data using fishnet aggregation
# method with a bounding polygon of 911 call data
# Process: Optimized Outlier Analysis
ooa = arcpy.stats.OptimizedOutlierAnalysis("Calls911", "Calls911_ohsaFishnet",
"#", "COUNT_INCIDENTS_WITHIN_FISHNET_POLYGONS",
"Calls911_MBG", "#",
"BALANCED_499")
except arcpy.ExecuteError:
# If any error occurred when running the tool, print the messages
print(arcpy.GetMessages())Environments
Special cases
- Output Coordinate System
Feature geometry is projected to the Output Coordinate System prior to analysis. All mathematical computations are based on the Output Coordinate System spatial reference. When the Output Coordinate System is based on degrees, minutes, and seconds, geodesic distances are estimated using chordal distances.
- Random number generator
The Random Generator Type used is always Mersenne Twister.
Licensing information
- Basic: Yes
- Standard: Yes
- Advanced: Yes
Related topics
- An overview of the Mapping Clusters toolset
- Modeling spatial relationships
- What is a z-score? What is a p-value?
- Spatial weights
- Spatial Autocorrelation (Global Moran's I)
- How Optimized Outlier Analysis works
- Cluster and Outlier Analysis (Anselin Local Moran's I)
- Hot Spot Analysis (Getis-Ord Gi*)
- Optimized Hot Spot Analysis
- Find a geoprocessing tool