Pour mesurer la tendance d'un ensemble de points ou de surface, il est courant de calculer la distance standard séparément dans les directions x, y et z. Ces mesures définissent les axes d'une ellipse (ou d'un ellipsoïde) englobant la distribution des entités. L'ellipse est désignée sous le nom d'ellipse d'écart type, car la méthode calcule l'écart type des coordonnées x et des coordonnées y à partir du centre moyen pour définir les axes de l'ellipse. En 3D, l'écart type des coordonnées z à partir du centre moyen est également calculé et le résultat est désigné sous le nom d'ellipsoïde d'écart type. L'ellipse ou l'ellipsoïde vous permet de voir si la distribution des entités est allongée et si elle a ainsi une orientation particulière.
Même si vous obtenir avoir un aperçu de l'orientation en dessinant les entités sur une carte, le calcul de l'ellipse d'écart type permet de mieux voir la tendance. Vous pouvez calculer l'ellipse d'écart type à l'aide de l'emplacement des entités ou de l'emplacement influencé par une valeur attributaire associée aux entités. La dernière possibilité est appelée ellipse d'écart type pondérée.
Calculs
L'ellipse d'écart type est calculée ainsi :
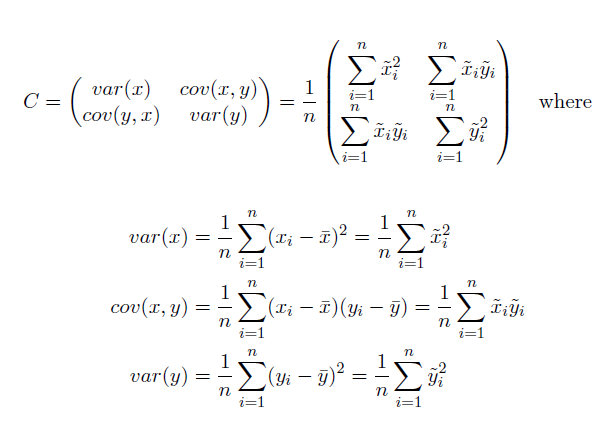
Où x et y sont les coordonnées de l'entité i, {x̄, ȳ} représentent le centre moyen des entités et n est égal au nombre total d'entités.
La matrice de covariance d'exemple est prise en charge dans une forme standard qui permet de représenter la matrice par ses valeurs propres et vecteurs propres. L'écart type des axes x et y est alors :
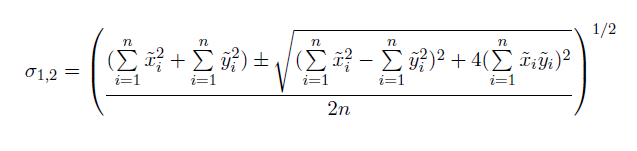
Ces équations peuvent être transformées en solutions pour les données tridimensionnelles.
Les variances sont mises à l'échelle selon un facteur d'ajustement afin de produire une ellipse ou un ellipsoïde contenant le pourcentage souhaité de points de données. Ces facteurs d'ajustement sont fournis dans la table ci-dessous.
| 1 donnée multidimensionnelle | 2 données multidimensionnelles | 3 données multidimensionnelles | |
|---|---|---|---|
1 écart type | 1.00 | 1.41 | 1.73 |
2 écarts types | 2.00 | 2.83 | 3.46 |
3 écarts types | 3.00 | 4.24 | 5.20 |
Consultez les ressources supplémentaires pour en savoir plus sur les valeurs propres et les vecteurs propres.
Sortie et interprétation
L'écart type vous aide à comprendre la dispersion ou la répartition de vos données. Si vous utilisez des données unidimensionnelles, la règle des trois sigmas communique généralement le pourcentage des valeurs de données qui seront comprises au sein d'un, deux et trois écarts types de la moyenne. Dans une distribution normale, cela signifie que 68 %, 95 % et 99,7 % des valeurs de données seront respectivement comprises dans un, deux et trois écarts types. Toutefois, si vous utilisez des données spatiales de dimension supérieure (variables x, y et z), ce décompte de pourcentage est rarement observé. La règle plus appropriée qui découle de la distribution Rayleigh suggère qu'une ellipse d'écart type recouvre approximativement 63 pour cent des entités, deux écarts types contiennent approximativement 98 pour cent des entités et trois écarts types recouvrent approximativement 99.9 pour cent des entités en deux dimensions. De même, en trois dimensions (x, y et z), la règle de pourcentage est 61-99-100.
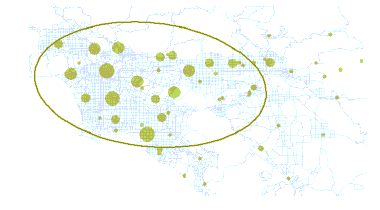
Pour les données en deux dimensions, l'outil Directional Distribution (Standard Deviational Ellipse) crée une nouvelle classe d'entités contenant un polygone elliptique centré sur le centre moyen pour toutes les entités (ou pour tous les cas où une valeur est spécifiée pour Champ de récapitulation). Les valeurs attributaires de ces polygones d'ellipse en sortie comprennent deux distances standard (axe long et axe court), l'orientation de l'ellipse et le champ de récapitulation, le cas échéant. L'orientation représente la rotation de l'axe long, mesurée dans le sens horaire à partir de midi. Vous pouvez également spécifier le nombre d'écarts types à représenter (1, 2 ou 3).
Pour les données ponctuelles en trois dimensions (vos données sont de type z et contiennent des informations attributaires 3D, telles qu'une altitude), cet outil crée un multipatch ellipsoïdal centré sur le centre moyen pour toutes les entités (ou pour tous les cas où une valeur est spécifiée pour Champ de récapitulation). Les valeurs attributaires de ces ellipsoïdes en sortie comprennent trois distances standard (axe long, axe court et axe de hauteur), des informations concernant l'angle, l'inclinaison et le roulis de l'ellipsoïde, ainsi que le champ de récapitulation, le cas échéant. Les valeurs de l'angle, de l'inclinaison et du roulis de l'ellipsoïde sont des angles d'Euler qui décrivent l'orientation de l'ellipsoïde dans l'espace 3D. Vous pouvez également spécifier le nombre d'écarts types à représenter (1, 2 ou 3).
Applications possibles
- Cartographier la tendance de distribution d'un ensemble de délits peut permettre d'identifier la relation à des entités physiques particulières (une chaîne de barres ou de restaurants, un boulevard en particulier, etc.).
- Cartographier des échantillons de puits souterrains à la recherche d'un polluant en particulier peut permettre d'indiquer la propagation de la toxine et par conséquent, peut être utile pour mettre en place des solutions.
- La comparaison de la taille, de la forme et de la superposition des ellipses pour différents groupes raciaux et ethniques peut offrir un aperçu de la ségrégation raciale ou ethnique.
- Le tracé d'ellipses concernant une épidémie au fil du temps peut être utile pour modéliser son évolution.
- L'examen de la distribution des altitudes pour les tempêtes d'une catégorie donnée peut constituer un facteur utile à prendre en compte pour en savoir plus sur la relation entre les conditions atmosphériques et les accidents d'avion.
Ressources supplémentaires
Chew, Victor. "Confidence, prediction, and tolerance regions for the multivariate normal distribution." Journal of the American Statistical Association 61.315 (1966): 605-617.
Fisher, N. I., T. Lewis, and B. J. J. Embleton. Statistical Analysis of Spherical Data. 1st ed. Cambridge: Cambridge University Press, 1987. Cambridge Books Online. Web. 26 April 2016.
Levine, Ned. "CrimeStat III: a spatial statistics program for the analysis of crime incident locations (version 3.0)." Houston (TX): Ned Levine & Associates/Washington, DC: National Institute of Justice (2004).
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
Wang, Bin, Wenzhong Shi, and Zelang Miao. (2015) Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space. PLoS ONE 10(3), e0118537.
Vous avez un commentaire à formuler concernant cette rubrique ?