Funktion "Trend generieren"

Mit der Image Analyst-Lizenz verfügbar.

Übersicht

Schätzt den Trend für jedes Pixel entlang einer Dimension für eine oder mehrere Variablen in einem multidimensionalen Raster.

Hinweise

Die unterstützten multidimensionalen Raster-Datasets sind netCDF, GRIB, HDF und Esri CRF. Multidimensionale Mosaik-Datasets werden auch unterstützt.

Die Ausgabe ist ein multidimensionaler Raster-Layer, wobei jeder Ausschnitt ein Multiband-Raster darstellt und Informationen über die Trendlinie enthält. Wenn Sie den Trend für eine einzelne Variable in einem Dataset analysieren, das eine einzelne Dimension (z. B. Zeit) enthält, enthält das Ausgabe-Dataset einen einzelnen Ausschnitt. Wenn Sie eine einzelne Variable eines Datasets analysieren, das mehrere Dimensionen enthält (z. B. Zeit und Tiefe), enthält jeder Ausschnitt Trendinformationen für alle Dimensionswerte.

Das mit dieser Funktion generierte Ausgabe-Trend-Raster wird als Eingabe für die Funktion Mit Trend vorhersagen verwendet.

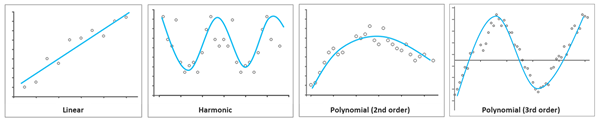
Es gibt drei Möglichkeiten der Anpassung eines Trends an die Variablenwerte entlang einer Dimension: linear, polynomisch und harmonisch. Diese drei Anpassungsoptionen für Trends werden nachfolgend beschrieben.

In der linearen Trendanalyse enthält die Ausgabe Dreiband-Raster. Hierbei gilt:

• Band 1 = Neigung
• Band 2 = Schnittpunkt
• Band 3 = RMS-Fehler (Root Mean Square, quadratisches Mittel) oder Fehler um die am besten passende Linie herum

In der polynomischen Trendanalyse hängt die Anzahl an Bändern in der Ausgabe von der Polynom-Ordnung ab. Bei der Polynomanpassung zweiter Ordnung entsteht ein Vierband-Raster. Hierbei gilt:

• Band 1 = Polynomial_2
• Band 2 = Polynomial_1
• Band 3 = Polynomial_0
• Band 4 = RMSE

Bei der Polynomanpassung dritter Ordnung entsteht ein Fünfband-Raster. Hierbei gilt:

• Band 1 = Polynomial_3
• Band 2 = Polynomial_2
• Band 3 = Polynomial_1
• Band 4 = Polynomial_0
• Band 5 = RMSE

In der harmonischen Trendanalyse hängt die Anzahl an Bändern in der Ausgabe von der harmonischen Frequenz ab. Bei der Frequenz 1 ist die Ausgabe ein Fünfband-Raster. Hierbei gilt:

• Band 1 = Neigung
• Band 2 = Schnittpunkt
• Band 3 = Harmonic_sin1
• Band 4 = Harmonic_cos1
• Band 5 = RMSE

Bei der Frequenz 2 ist die Ausgabe ein Siebenband-Raster. Hierbei gilt:

• Band 1 = Neigung
• Band 2 = Schnittpunkt
• Band 3 = Harmonic_sin1
• Band 4 = Harmonic_cos1
• Band 5 = Harmonic_sin2
• Band 6 = Harmonic_cos2
• Band 7 = RMSE

Mit dem Parameter Zykluslänge für die harmonische Trendanalyse wird die Anzahl und Länge der Zyklen angegeben, die Sie für die Daten in einem Tag oder Jahr erwarten. Wenn Sie beispielsweise für Ihre Daten zwei Variationszyklen pro Jahr erwarten, beträgt die Zykluslänge 182,5 Tage bzw. 0,5 Jahre. Wenn alle drei Stunden eine Erfassung von Temperaturdaten erfolgt und pro Tag ein Variationszyklus vorliegt, beträgt die Zykluslänge einen Tag.

Mit dem Parameter Häufigkeit für die harmonische Trendanalyse wird das harmonische Modell beschrieben, das an die Daten angepasst wird. Wird die Häufigkeit auf 1 festgelegt, wird eine Kombination aus linearer Kurve und harmonischer Kurve der ersten Ordnung für die Anpassung des Modells verwendet. Beträgt die Häufigkeit 2, wird eine Kombination aus linearer Kurve, harmonischer Kurve der ersten Ordnung und harmonischer Kurve der zweiten Ordnung für die Anpassung des Modells verwendet. Beträgt die Häufigkeit 3, wird zusätzlich eine harmonische Kurve der dritten Ordnung für die Modellierung der Daten verwendet und so weiter und so fort.

Modellstatistiken zur Qualität der Übereinstimmung können als optionale Ausgabe generiert werden. Der RMS-Fehler (Root Mean Square, quadratisches Mittel), R-Squared und der Trend für den p-Wert der Neigung können berechnet und symbolisiert werden. Symbolisieren Sie den Ausgabe-Trend-Raster-Layer mit der Symbolisierung RGB, und geben Sie die Statistiken als rote, grüne und blaue Bänder an.

Parameter

Parameter	Beschreibung
Raster	Das als Eingabe verwendete multidimensionale Raster.
Dimensionsname	Die Dimension, für die anhand der in der Analyse ausgewählte(n) Variable(n) Trenddaten gewonnen werden sollen.
Regressionstyp	Gibt den Linientyp für die Anpassung an die Pixelwerte in einer Dimension an. Linear: Passt die Pixelwerte für eine Variable entlang einer linearen Trendlinie an. Dies ist die Standardeinstellung. Harmonisch: Passt die Pixelwerte für eine Variable entlang einer harmonischen Trendlinie an. Polynomisch: Passt die Pixelwerte für eine Variable entlang einer polynomischen Trendlinie an.
Harmonische Frequenz	Die für die Trendanpassung verwendete Frequenz. Dieser Parameter gibt die Frequenz als Zyklen pro Jahr an. Der Standardwert ist 1, das entspricht einem harmonischen Zyklus pro Jahr. Dieser Parameter ist nur bei harmonischer Regression in der Trendanalyse enthalten.
Zykluslänge	Die Länge der zu modellierenden periodischen Variation. Die Einheit ist stets Tage; die Zeiteinheit der Eingabedaten ist unerheblich. Der Grünanteil bei Blättern beispielsweise weist pro Jahr einen starken Variationszyklus auf, sodass die Zykluslänge 365,25 beträgt, obwohl die Eingabedaten als monatlich erfasster Grünanteil vorliegen. Stündlich erfasste Temperaturdaten weisen pro Tag einen starken Variationszyklus auf, sodass die Zykluslänge 1 beträgt. Für Daten, die eine Variation auf Grundlage eines Jahreszyklus aufweisen, beträgt die Standardlänge 365,25 Tage.
Zykluseinheit	Gibt die Zeiteinheit für die Länge eines harmonischen Zyklus an. Tage: Die Einheit für die Länge des harmonischen Zyklus ist ein Tag. Jahre: Die Einheit für die Länge des harmonischen Zyklus ist ein Jahr. Dies ist die Standardeinstellung.
Polynom-Ordnung	Die für die Trendanpassung verwendete Polynom-Ordnung. Dieser Parameter gibt die Polynom-Ordnung an. Der Standardwert ist 2, das entspricht einem Polynom zweiter Ordnung. Dieser Parameter ist nur bei polynomischer Regression in der Trendanalyse enthalten.
NoData ignorieren	Gibt an, ob NoData-Werte bei der Analyse ignoriert werden. Aktiviert: Bei der Analyse werden alle gültigen Pixel entlang einer angegebenen Dimension einbezogen und alle NoData-Pixel ignoriert. Dies ist die Standardeinstellung. Deaktiviert: Wenn NoData-Werte für die Pixel entlang einer angegebenen Dimension vorhanden sind, wird bei der Analyse NoData zurückgegeben.
RMSE	Gibt an, ob der RMS-Fehler (Root Mean Square, quadratisches Mittel) der angepassten Trendlinie erstellt wird. Aktiviert: Der RMS-Fehler wird bei Abschluss der Funktion berechnet und in den Details angezeigt. Dies ist die Standardeinstellung. Deaktiviert: Der RMS-Fehler wird nicht berechnet.
R-Squared	Gibt an, ob für die angepasste Trendlinie eine Statistik zur Qualität der Übereinstimmung von R-Squared erstellt wird. Aktiviert: R-Squared wird bei Abschluss der Funktion berechnet und in den Details angezeigt. Deaktiviert: R-Squared wird nicht berechnet. Dies ist die Standardeinstellung.
P-Wert des Neigungskoeffizienten	Gibt an, ob die p-Wertstatistik für den Neigungskoeffizienten der Trendlinie berechnet wird. Aktiviert: Der p-Wert wird bei Abschluss der Funktion berechnet und in den Details angezeigt. Deaktiviert: Der p-Wert wird nicht berechnet. Dies ist die Standardeinstellung.

Regressionstypen

Die Regressionsgleichung für jede Trendoption ist nachfolgend aufgeführt.

• Linear: Die lineare Trendlinie ist eine am besten passende gerade Linie, die zur Schätzung einfacher linearer Beziehungen verwendet wird. Ein linearer Trend kennzeichnet eine gleichbleibende Veränderung nach oben oder unten. Die Formel für lineare Trendlinien lautet wie folgt:

  

  • y = Variablenwert des Pixels
  • x = Dimensionswert
  • ß0 = y-Schnittpunkt
  • ß1 = lineare Neigung oder Änderungsrate

    ß1 > 0 weist auf einen zunehmenden Trend hin.

    ß1 < 0 weist auf einen abnehmenden Trend hin.

• Polynomisch: Die polynomische Trendlinie ist eine geschwungene Linie, die gut zur Darstellung von Daten mit stärkerer Fluktuation geeignet ist. In diesem Fall wird die maximale Anzahl der auftretenden Fluktuationen durch eine Polynom-Ordnung angegeben. Die Formel für polynomische Trendlinien lautet wie folgt:

  

  • y = Variablenwert des Pixels
  • x = Dimensionswert
  • ß0, ß1, ß2, ß3, ... ßn = konstante Koeffizienten
• Harmonisch: Die harmonische Trendlinie ist eine sich periodisch wiederholende geschwungene Linie; mit ihr lassen sich Daten beschreiben, die einem Zyklus folgen, z. B. saisonal bedingte Temperaturänderungen. Die Formel für harmonische Trendlinien lautet wie folgt:

  

  • y = Variablenwert des Pixels
  • t = Datum nach Julianischem Kalender
  • ß0 = y-Schnittpunkt
  • ß1 = Veränderungsrate
  • α, γ = Koeffizienten der Veränderungen innerhalb eines Jahres oder jahresübergreifend
  • ω = i
  • f = harmonische Frequenz