Funktionsweise von "Durchlässigkeit"

Mit der Spatial Analyst-Lizenz verfügbar.

Der Lösungstransport in einem porösen Medium beruht auf zwei grundlegenden Mechanismen: Advektion und hydrodynamische Dispersion. Advektion beschreibt den passiven Transport eines gelösten Stoffes in der Transportflüssigkeit. Dispersion bedeutet die Durchmischung des gelösten Stoffes und der Transportflüssigkeit, die in Porenräumen aufgrund der unterschiedlichen Partikelbewegung der Flüssigkeiten auftritt. Beim Werkzeug Durchlässigkeit wird davon ausgegangen, dass der Grundwasserleiter vertikal gemischt ist. Angenommen wird also, dass die Konzentration in einem senkrechten Abschnitt des Leiters an jeder Stelle gleich ist. Dadurch kann ein zweidimensionales mathematisches Modell angewendet werden, was eine Voraussetzung für das Raster-Datenmodell ist.

Zweidimensionale Dispersion

Die zweidimensionale Dispersion in einem porösen Medium wird durch die Advektions-Dispersions-Gleichung (Bear, 1979; Freeze/Cherry, 1979; Marsily, 1986) beschrieben, die in Bezug auf die Längsrichtung X_L (in Fließrichtung) und die Querrichtung X_T (senkrecht zur Fließrichtung) ausgedrückt wird:

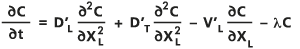
• Dabei gilt:

  C: Die Konzentration des gelösten Stoffes als Funktion zweier räumlicher Dimensionen und der Zeit t.

  ∂C/∂t: Stellt die zeitliche Änderung dar.

  D'_L: Der effektive (verzögerte) Dispersionskoeffizient in Fließrichtung.

  D'_T: Der effektive (verzögerte) Dispersionskoeffizient senkrecht zur Fließrichtung.

  λ: Der Zerfallskoeffizient; für exponentiellen Zerfall erster Ordnung wird er als konstant angenommen.

Dispersionskoeffizienten

Der Dispersionskoeffizient ist ein Maß der Verteilung des gelösten Stoffes in der angegebenen Richtung:

D'_i = D_i/R

• Dabei gilt:

  R: Der Retardationsfaktor.

  i: Die Richtung (in Fließrichtung oder senkrecht zur Fließrichtung).

Der Dispersionskoeffizient steht mit dem Verhalten eines gelösten Stoffes in einem bestimmten Medium in Zusammenhang.

Verhältnis zwischen Dispersivität und Dispersionskoeffizient

Die Dispersivitäten α_L (Dispersivität in Fließrichtung) und α_T (abgeleitet aus dem Dispersivitätsverhältnis) stehen folgendermaßen mit den Dispersionskoeffizienten in Verhältnis:

D'_L = α_L V' und

D'_T = α_T V'

• Dabei gilt:

  V': Die durchschnittliche verzögerte Geschwindigkeit der Transportflüssigkeit.

  X_L: Die Verdrängung in Längsrichtung, parallel zur Fließrichtung am Massenschwerpunkt.

  X_T: Die Verdrängung in Querrichtung, rechtwinklig zur Fließrichtung am Massenschwerpunkt.

  V'_L: Die verzögerte Geschwindigkeit des gelösten Stoffes in Fließrichtung.

Transportgeschwindigkeiten

Im Grundwasserfluss:

V = q/n

• Dabei gilt:

  q: Die Darcy-Geschwindigkeit (Ablauf per Querschnittsfläche).

  n: Die effektive Porosität der geologischen Formation.

V' = V/R

Eine nähere Betrachtung der Transportgeschwindigkeiten finden Sie unter Darcy-Geschwindigkeit.

Gauß'sche Dispersion

Die Näherungslösung der in Durchlässigkeit verwendeten Gleichung basiert auf der Annahme einer Gauß'schen Streuung für eine unverzögert freigesetzte Punktquelle in einer zweidimensionalen Domäne. Anfangskonzentration ist dabei null (z. B. ein sauberer, vertikal gemischter Grundwasserleiter). Die Lösung wird mit der folgenden Gleichung berechnet:

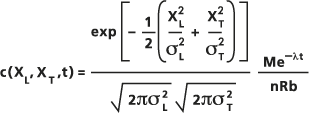
• Dabei gilt:

  M: Die Masse des gelösten Stoffes, der unverzögert an der Quelle freigegeben wird, in Masseneinheiten.

  n: Die Porosität des Grundwasserleiters.

  R: Der Retardationsfaktor.

  b: Die Mächtigkeit des Grundwasserleiters in Längeneinheiten.

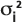  : Die Varianz der Gauß'schen Verteilung in Längs- und Querrichtung, bestimmt als Funktion der Dispersivität in Fließrichtung und des angegebenen Dispersivitätsverhältnisses sowie der Länge der Transportstrecke des gelösten Stoffes am Massenmittelpunkt. Die Längenangaben werden dabei aus der Datei für die Partikelverfolgung abgerufen.

Nachstehend finden Sie eine allgemeine Abbildung der elliptischen Form dieser zweidimensionalen Gauß'schen Verteilungsfunktion:

Form der zweidimensionalen Gauß'schen Verteilung

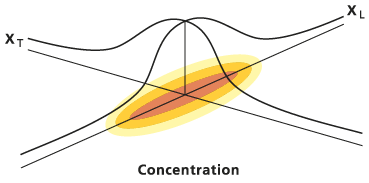
Es sind mehrere Einschränkungen bei der Lösung von Durchlässigkeit zu beachten. Auch die zugrunde liegenden Annahmen müssen berücksichtigt werden. Das Zentrum der Verteilungsellipse befindet sich in der Masse des gelösten Stoffes. Von diesem wird angenommen, dass er sich entlang dem in der Eingabedatei beschriebenen Fließpfad bewegt hat. Die Ausrichtung der Ellipse wird ebenfalls durch den Fließpfad bestimmt: Die Hauptachse bildet am Schwerpunkt eine Tangente zum Fließpfad. Porosität und Mächtigkeit, die die Verteilung ebenfalls beeinflussen, werden aus den entsprechenden Rastern am Schwerpunkt interpoliert. Dabei werden keine Informationen aus den umgebenden Zellen einbezogen. Retardation, Zeit, Zerfallskoeffizient, Dispersivität in Fließrichtung und Dispersivitätsverhältnis werden vom Benutzer als Konstanten angegeben.

Dispersivität

Die Dispersivität ist ein Parameter, der die Dispersion eines gelösten Stoffes in einem porösen Medium bestimmt. Sie wird in Längeneinheiten angegeben. Im Modell Durchlässigkeit wird die Dispersivität zur Berechnung der Varianz 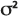der obigen Gauß'schen Streuungsgleichung verwendet. Sie wird folgendermaßen berechnet:

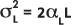• und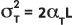
• 

Die Eigenschaften und Berechnungsmethoden der Dispersivität sind von großem Interesse bei der Grundwassermodellierung, sorgen aber gleichzeitig für Kontroverse innerhalb des Fachkreises. Derzeit gibt es keine allgemein anerkannte Herangehensweise für die Schätzung der Dispersivitätswerte. Eine Betrachtung der Dispersivitäten in verschiedenen geologischen Formationen finden Sie in Gelhar et al. (1992).

Im folgenden Diagramm sind verschiedene Daten aus veröffentlichten Literaturwerken zusammengefasst. Die Dispersivität in Fließrichtung wird mit dem Maßstab des Untersuchungsgegenstands in Bezug gesetzt, d. h. mit der Entfernung zwischen Quellenposition und Beobachtungspunkt.

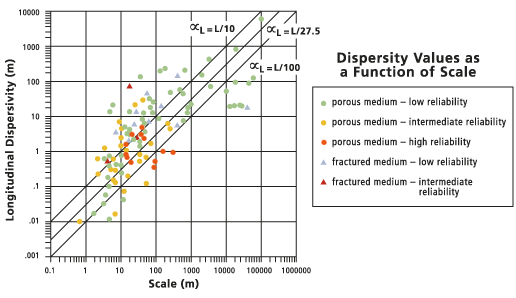
• Die durchgezogene Linie (die Mittellinie) im Diagramm stellt den Standardwert der Dispersivität in Fließrichtung dar, der vom Werkzeug "Durchlässigkeit" berechnet wurde.

  Diese Linie wird durch eine lineare Regressionsanpassung von 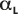zu L erstellt. Ergebnis ist 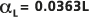oder 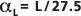, wobei die Länge der Transportstrecke L dem Beobachtungsmaßstab entspricht.

  Die Statistiken zu dieser Regression werden ebenfalls angezeigt. Die äußeren gepunkteten Linien werden zum Vergleich an den Positionen 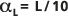und 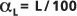platziert.

Diese Standardberechnung sollte nur als Richtlinie verwendet werden, da von einer derartigen Universallösung von einigen Forschern abgeraten wird. Für denselben Maßstab bzw. dieselbe Position können sich die Dispersivitätswerte um bis zu zwei Größenordnungen unterscheiden. Tendenziell liegen dabei die zuverlässigeren Schätzwerte im unteren Bereiche. Anstatt den Standardwert, der nicht auf einer theoretischen Grundlage beruht, zu verwenden, sollten Sie mehrere Simulationen mit verschiedenen Dispersivitätswerten durchführen. Durch die Berücksichtigung von mehreren Ergebnissen kann eine höhere Zuverlässigkeit erzielt werden als durch die Verwendung der Ergebnisse einer einzelnen Simulation.

Ähnliches ist bei der Schätzung des Verhältnisses der Dispersivität in Fließrichtung zur Dispersivität senkrecht zur Fließrichtung zu beachten, wie in der nachfolgenden Abbildung dargestellt. Diese Werte stehen gewöhnlich in einem einfachen Verhältnis zueinander. Sie sollten jedoch wie bereits erwähnt verschiedene Wertebereiche heranziehen.

Vergleich von Dispersivitäten

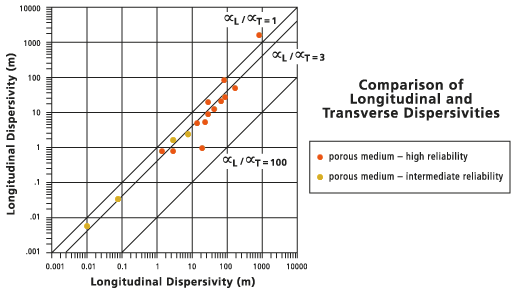
Das standardmäßige Dispersivitätsverhältnis 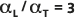ist in der unten stehenden Abbildung durch die durchgezogene Linie (die Mittellinie) dargestellt. Die gepunkteten Linien (die äußeren Linien) werden zum Vergleich bei 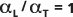und 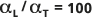platziert.

Werte der effektiven Porosität und Transmissivität

Gelhar et al. beziehen die Werte der effektiven Porosität und Transmissivität in ihre Berechnungen ein. Tabellen zu diesen Werten finden Sie in Freeze/Cherry (1979) und Marsily (1986).

Retardation

Die Retardation ist das Verhältnis zwischen der Geschwindigkeit der Transportflüssigkeit und der Geschwindigkeit des gelösten Stoffes. Sie wird ohne Einheit als eine Zahl zwischen eins und unendlich angegeben. Eine Retardation von 2 bedeutet, dass der gelöste Stoff bei halber Sickergeschwindigkeit durch die Poren des porösen Mediums sickert. Ein idealer Tracer erfährt keine Adsorption und bewegt sich zusammen mit der Flüssigkeit in der Lösung. Ein solcher gelöster Stoff weist eine Retardation von 1 auf, was bedeutet, dass er sich mit derselben Geschwindigkeit wie die Transportflüssigkeit bewegt.

Dieses Phänomen ist das Ergebnis der Adsorption und Desorption des Stoffes durch die poröse Matrix, insbesondere durch organische Stoffe an der Oberfläche der Porenwände. Die Retardationsgleichung wird in einer Abhandlung von Freeze und Cherry (1979) vorgestellt als:

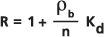
• Dabei gilt:

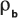  : Die Rohdichte der Matrix.

  n: Die Porosität der Formation.

  K_d: Der Verteilungskoeffizient, der die Verteilung eines gelösten Stoffes in flüssigen und festen Phasen aufgrund einer schnellen, umkehrbaren Adsorption darstellt. Vorausgesetzt wird dabei eine lineare Isotherme.

Marsily (1986) betrachtet ebenfalls detailliert das Thema Retardationsfaktor und Adsorption.

Ausführen der Advektions-Dispersions-Modellierung

Mit den Werkzeugen Darcy-Strömung, Partikelverfolgung und Durchlässigkeit kann eine grundlegende Advektions-Dispersions-Modellierung der Grundwasserbestandteile vorgenommen werden. Anhand von Darcy-Strömung wird aus geologischen Daten ein Geschwindigkeitsfeld des Grundwasserflusses erstellt. Mithilfe von Partikelverfolgung wird ausgehend von einer Punktquelle der Advektionspfad durch das Fließfeld verfolgt. Anschließend wird mit Durchlässigkeit die hydrodynamische Dispersion eines unverzögert freigesetzten Stoffes berechnet, der entlang des Fließpfades advektiert wird.

Eine vollständige Abhandlung zum Thema Advektions-Dispersions-Modellierung unter Verwendung dieser Werkzeuge ist in Tauxe (1994) zu finden.

Bei der Grundwassermodellierung werden die Werkzeuge gewöhnlicherweise in folgender Reihenfolge eingesetzt: Darcy-Strömung, Partikelverfolgung und Durchlässigkeit.

Beispiele

• Nachfolgend wird ein Beispiel für das Dialogfeld des Werkzeugs Durchlässigkeit gegeben:

  Eingabe-Datei der Partikelverfolgung: ttrack.txt

  Eingabe-Raster der effektiven Porosität der Formation: poros

  Eingabe-Raster der gesättigten Stärke: thickn

  Ausgabe-Raster: ppuff1

  Masse: 3.2e7

  Zeithorizont für die Dispersion: 50000

  Dispersivität in Fließrichtung: 6

  Dispersivitätsverhältnis: 3

  Retardationsfaktor: 1

  Zerfallskoeffizient: 250

• Das folgende Beispiel veranschaulicht die Verwendung von Durchlässigkeit in Map Algebra:

  outPPuff1 = PorousPuff(ttrack.txt, poros, thickn, 1000000, 0.01, 10, 1.5, 1.0, 500)

• Im Folgenden finden Sie eine Reihe von Map Algebra-Ausdrücken für die Werkzeuge der Grundwassermodellierung:

  out_vol = DarcyFlow(head, poros, thickn, transm, dir1, mag1)
  ParticleTrack(dir1, mag1, ttrack.txt, 500, 650, "#", "#", track_feat.shp)
  out_puff = PorousPuff(ttrack.txt, poros, thickn, 3.2e7, 50000, 6, 3, 1, 250)

Referenzen

Bear, J. 1979, Hydraulics of Groundwater. McGraw-Hill.

Freeze, R. A., and J. A. Cherry. 1979. Groundwater. Prentice Hall.

Gelhar, L. W., C. Welty, and K. R. Rehfeldt. 1992. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research 28 (7): 1955-1974.

Marsily, G. de. 1986. Quantitative Hydrogeology. Academic Press.

Tauxe, J. D. 1994. "Porous Medium Advection–Dispersion Modeling in a Geographic Information System". Ph.D. diss., University of Texas, Austin.