Beschreibung
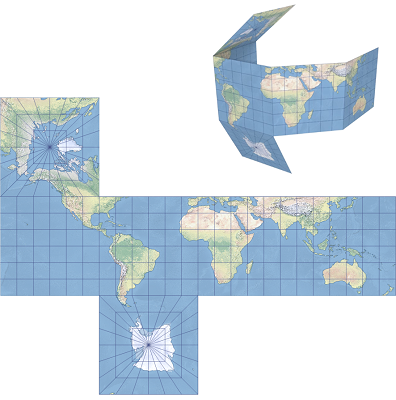
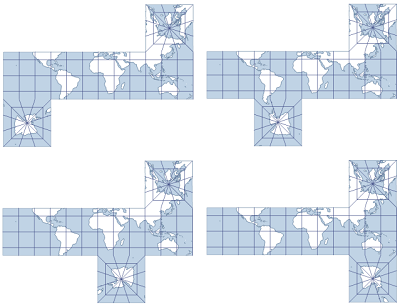
Die Würfelprojektion ist eine Facettenprojektion, die aus sechs quadratischen Seiten besteht: eine für jeden Pol und vier entlang des Äquators, zentriert auf die westlichen Meridiane 135° und 45° sowie die östlichen Meridiane 45° und 135°. Sie kann zu einem Würfel gefaltet werden. Flächen zwischen 45° Nord und 45° Süd werden mit der Plate-Carrée-Projektion projiziert.
Die Würfelprojektion ist in ArcGIS Pro 1.0 und höher sowie in ArcGIS Desktop 9.0 und höher verfügbar.
Projektionseigenschaften
In den folgenden Unterabschnitten werden die Eigenschaften der Würfelprojektion beschrieben.
Gradnetz
Die Würfelprojektion ist eine Facettenprojektion. Die Meridiane und Parallelkreise sind gerade Linien mit gleichen Abständen, liegen zwischen 45° Nord und 45° Süd und bilden ein Raster perfekter Quadrate. Die polaren Facetten projizieren Parallelkreise als konzentrische Quadrate mit dem Pol, einem Punkt, als Mittelpunkt. Die Meridiane sind gerade Linien mit gleichen Abständen, deren Ursprung der Mittelpunkt ist. Der Umriss der polaren Facette ist ein Quadrat des 45°-Parallelkreises. Am Schnittpunkt der Äquatorfacette mit den polaren Facetten neigen sich die Meridiane Richtung Pol. Bei bestimmten Anordnungen der polaren Facetten kann das Gradnetz über dem Äquator und/oder Mittelmeridian symmetrisch sein.
Verzerrung
Die Würfelprojektion ist weder winkeltreu noch flächentreu. Formen, Flächen, Entfernungen, Richtungen und Winkel sind im Allgemeinen verzerrt. Zwischen 45° Nord und 45° Süd folgen die Verzerrungseigenschaften der Plate-Carrée-Projektion. Verzerrungen von Formen, Maßstab und Flächen werden mit zunehmender Entfernung vom Äquator größer. Die Richtungen Norden, Süden, Osten und Westen sind immer korrekt. Allgemeine Richtungen sind jedoch verzerrt, außer lokal am Äquator. In den polaren Facetten sind die Richtungen vom Mittelpunkt aus korrekt. Der Maßstab ist am Äquator korrekt.
Verwendung
Für die allgemeine Kartenerstellung ist die Würfelprojektion nicht empfehlenswert.
Beschränkungen
Die Würfelprojektion wird nur für Kugeln unterstützt. Für Ellipsoide wird als Radius die große Halbachse verwendet. Bei Verwendung eines Ellipsoids werden manche Eigenschaften der Äquidistanz und Richtung nicht beibehalten.
Parameter
Die Würfelparameter lauten wie folgt:
- Östlicher Versatz
- Nördlicher Versatz
- Mittelmeridian
- In der folgenden Tabelle wird die verwendete Option zum Anzeigen verschiedener Anordnungen der polaren Facetten mit den folgenden Werten aufgeführt. In den Beispielen wird der Standardwert des Mittelmeridians 0° verwendet.
Optionswerte Beschreibung Beispiel 0, 1, 2 oder 3.
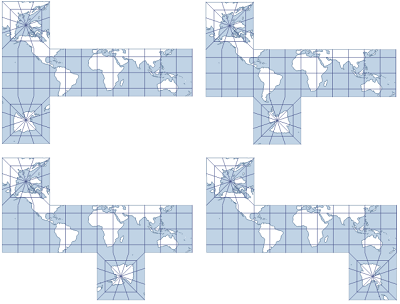
Die Facette des Nordpols ist an dem Meridian ausgerichtet, der sich 135° westlich des Mittelmeridians befindet.
Die Facette des Südpols ist an 135° West, 45° West, 45° Ost bzw. 135° Ost ausgehend vom Mittelmeridian ausgerichtet.
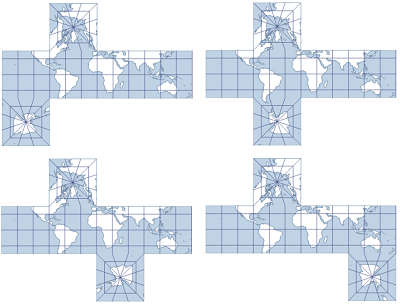
4, 5, 6 oder 7.
Die Facette des Nordpols ist an dem Meridian ausgerichtet, der sich 45° westlich des Mittelmeridians befindet.
Die Facette des Südpols ist an 135° West, 45° West, 45° Ost bzw. 135° Ost ausgehend vom Mittelmeridian ausgerichtet.
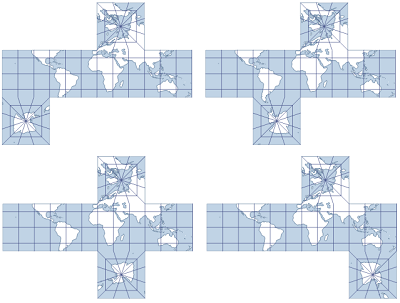
8, 9, 10 oder 11.
Die Facette des Nordpols ist an dem Meridian ausgerichtet, der sich 45° östlich des Mittelmeridians befindet.
Die Facette des Südpols ist an 135° West, 45° West, 45° Ost bzw. 135° Ost ausgehend vom Mittelmeridian ausgerichtet.
12, 13, 14 oder 15.
Die Facette des Nordpols ist an dem Meridian ausgerichtet, der sich 135° östlich des Mittelmeridians befindet.
Die Facette des Südpols ist an 135° West, 45° West, 45° Ost bzw. 135° Ost ausgehend vom Mittelmeridian ausgerichtet.
Quellen
Keine verfügbare öffentlichen Quellen.