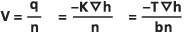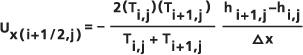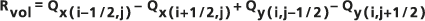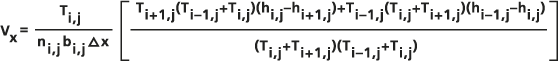Mit der Spatial Analyst-Lizenz verfügbar.
Darcy-Strömung und Darcy-Geschwindigkeit können in Verbindung mit Partikelverfolgung und Durchlässigkeit verwendet werden, um eine rudimentäre Advektions-Dispersions-Modellierung von Grundwasserbestandteilen vorzunehmen. Diese Methode modelliert einen zweidimensionalen, senkrecht gemischten, horizontalen und gleichmäßigen Fluss, bei dem das Druckpotenzial unabhängig von der Tiefe ist.
Berechnung der Darcy-Strömung
Die bei der Berechnung der Darcy-Strömung verwendeten Gleichungen werden in den folgenden Abschnitten beschrieben.
Berechnen von Fluss und Geschwindigkeit
Das Darcy-Gesetz besagt, dass die Darcy-Geschwindigkeit q in einem porösen Medium anhand der hydraulischen Leitfähigkeit K und dem hydraulischen Gradienten
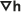(die Änderung des Druckpotenzials pro Einheit Länge in der Strömungsrichtung in einem isotropischen Grundwasserleiter) wie folgt berechnet wird:- q = -K
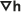
wobei K aus der Transmissivität T und der Stärke b als K = T/b berechnet werden kann.
Dieser Wert q, in Einheiten von Volumen/Zeit/Fläche, wird auch als spezifischer Durchfluss, volumetrischer Durchfluss oder Filtergeschwindigkeit bezeichnet. Bear (1979) definiert ihn als das Volumen des Wassers, das in der normalen Strömungsrichtung pro Einheit Zeit durch eine Einheit Querschnittsfläche fließt.
- q = -K
Eng verknüpft mit dem volumetrischen Durchfluss ist der Durchfluss U des Grundwasserleiters, wobei es sich um den Abfluss pro Einheit Breite im Grundwasserleiter handelt (in Einheiten von Volumen/Zeit/Länge):
- U = -T
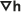
Dieses Konzept geht davon aus, dass das Druckpotenzial von der Tiefe unabhängig ist, sodass der Fluss horizontal ist.
- U = -T
Die durchschnittliche Flüssigkeitsgeschwindigkeit innerhalb der Poren, bezeichnet als Sickergeschwindigkeit V, ist die Darcy-Geschwindigkeit geteilt durch die effektive Porosität des Mediums:
In der Implementierung des Werkzeugs Darcy-Strömung wird die Sickergeschwindigkeit V auf Zellenbasis berechnet. Für eine Zelle i,j wird der Durchfluss U des Grundwasserleiters durch jede der vier Zellwände berechnet, wobei der Unterschied zwischen den Druckpotenzialen der zwei benachbarten Zellen und das harmonische Mittel der Transmissivitäten Ti+1/2,j (Konikow und Bredehoeft, 1978) verwendet wird, die als isotropisch vorausgesetzt werden.
Zum Beispiel lautet für die x-Komponente von
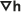die Gleichung zwischen den Zellen i,j und i+1,j:- δh/δx ≈ (hi+1 - hi) / Δx
Dieses Schema wird in den folgenden Grafiken veranschaulicht:
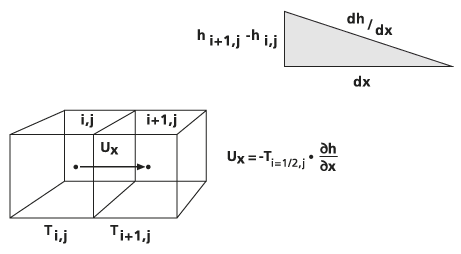
Berechnen des Restvolumens
In der darauffolgenden Zellwandberechnung erfolgt der Durchfluss des Grundwasserleiters zwischen Zelle i,j und Zelle i+1,j parallel zur x-Richtung. Er wird wie folgt berechnet:
Um den Grundwasservolumenausgleich zu bestimmen, muss der Grundwasserabfluss durch die Zellwand berechnet werden. Der Abfluss Q x(i+1/2) wird aus dem Durchfluss U des Grundwasserleiters und der Breite der Zellwand Δy berechnet:
- Qx(i+1/2,j) = Ux(i+1/2,j) Δy
Für alle vier Zellwände ergeben sich ähnliche Werte. Anhand dieser Werte wird für die Zelle das Residuum für den Grundwasservolumenausgleich Rvol berechnet, das in das Ausgabe-Raster geschrieben wird. Dieser Wert stellt den Überschuss (oder, im Fall einer negativen Zahl, das Fehlen) des Wassers in Abhängigkeit vom Nettofluss in die jeweilige Zelle dar. Er wird wie folgt berechnet:
Das Residuum Rvol sollte im Idealfall für alle Zellen 0 betragen. Achten Sie auf Abweichungen von 0, wenn Sie das Ausgabe-Raster mit den Residuen untersuchen. Große positive oder negative Residuen bedeuten eine Massenzunahme bzw. einen Massenverlust, was gegen den Grundsatz der Kontinuität verstößt und auf inkonsistente Druckpotenzial- und Transmissivitätsdaten hinweist. Konsistente Muster positiver oder negativer Residuen deuten darauf hin, dass nicht identifizierte Quellen oder Senken vorhanden sind. Vor jeder weiteren Modellierung sind die Residuen zu reduzieren. In der Regel werden dazu Anpassungen am Transmissivitätsfeld vorgenommen.
Berechnen von Flussvektoren
Die tatsächlich in Darcy-Strömung zum Berechnen der Flussvektoren für jede Zelle verwendeten Gleichungen werden vom arithmetischen Mittel von Ux(i-1/2,j) und Ux(i+1/2,j) abgeleitet, geteilt durch die Porosität der mittleren Zelle ni,j und der Stärke bi,jj, um einen Wert für die Sickergeschwindigkeit Vx im Mittelpunkt zu erhalten:
Eine ähnliche Gleichung wird verwendet, um V y im Mittelpunkt zu berechnen:
Durch diese Zentrierung wird die Konvention erfüllt, dass gespeicherte Werte Werte im Mittelpunkt der Zelle darstellen. Zur Speicherung in den Ausgabe-Richtungs- und Magnituden-Rastern werden diese Werte in Richtung und Magnitude für geographische Koordinaten konvertiert.
Im Falle der Grenzzellen des Rasters, für die die Informationen unvollständig sind, werden die Geschwindigkeitswerte aus der nächstgelegenen inneren Zelle kopiert.
Porositätswerte
In den folgenden Tabellen sind für verschiedene geologische Medien einige Werte hinsichtlich Porosität und hydraulischer Leitfähigkeit zusammengefasst.
Tabelle 1: Hydraulische Leitfähigkeiten nicht fundierter Medien
| Medium | K (m/s) |
|---|---|
Grober Kies | 10-1 – 10-2 |
Sand und Kies | 10-1 – 10-5 |
Feiner Sand, Schlicke, Löss | 10-5 – 10-9 |
Ton, Schiefer, Moränenablagerung | 10-9 – 10-13 |
Tabelle 2: Hydraulische Leitfähigkeiten fundierter Medien
| Medium | K (m/s) |
|---|---|
Dolomitkalk |
10-3 – 10-5 |
Verwitterter Kalk |
10-3 – 10-5 |
Unverwitterter Kalk |
10-6 – 10-9 |
Kalkstein |
10-5 – 10-9 |
Sandstein |
10-4 – 10-10 |
Granit, Gneis, kompakter Basalt |
10-9 – 10-13 |
Tabelle 3: Porositäten geologischer Medien
| Medium | Gesamtporosität |
|---|---|
Unveränderter Granit und Gneis | 0,0002–0,018 |
Quartzit | 0,008 |
Schiefer, Schieferplatten, Glimmerschiefer | 0,005–0,075 |
Kalkstein, Primärdolomit | 0,005–0,125 |
Sekundärdolomit | 0,10–0,30 |
Kreide | 0,08–0,37 |
Sandstein | 0,035–0,38 |
Vulkanischer Tuff | 0,30–0,40 |
Sand | 0,15–0,48 |
Ton | 0,44–0,53 |
Blähton, Schlick | bis zu 0,90 |
Bestellter Ackerboden | 0,45–0,65 |
Zusätzliche tabellarisierte Werte für Porosität und hydraulische Leitfähigkeit finden sich bei Freeze und Cherry (1979). Gelhar et al. (1992) geben eine Zusammenfassung der Porosität und Transmissivität verschiedener spezifischer Formationen, die in verschiedenen Literaturquellen aufgezeichnet sind. Eine ausführliche Darstellung der Porosität in sedimentären Materialien geben Blatt et al. (1980). Eine vollständige Abhandlung zum Thema Advektions-Dispersions-Modellierung unter Verwendung dieser Funktionen ist in Tauxe (1994) zu finden.
Beispiele
Bei der Grundwasser-Dispersionsmodellierung werden die Werkzeuge gewöhnlicherweise in folgender Reihenfolge eingesetzt: Darcy-Strömung, Partikelverfolgung und Durchlässigkeit.
- Im Folgenden finden Sie ein Beispiel für die Einstellungen, die im Dialogfeld des Werkzeugs Darcy-Strömung vorzunehmen sind:
Eingabe-Raster des Grundwasserdruckpotenzials: head
Eingabe-Raster der effektiven Porosität der Formation: poros
Eingabe-Raster der gesättigten Stärke: thickn
Eingabe-Raster der Transmissivität der Formation: transm
Ausgabe-Raster für Grundwasservolumenausgleich: resid1
Ausgabe-Richtungs-Raster: dir1
Ausgabe-Magnituden-Raster: mag1
- Im Folgenden finden Sie ein Beispiel für die Einstellungen, die im Dialogfeld des Werkzeugs Darcy-Geschwindigkeit vorzunehmen sind:
Eingabe-Raster des Grundwasserdruckpotenzials: head
Eingabe-Raster der effektiven Porosität der Formation: poros
Eingabe-Raster der gesättigten Stärke: thickn
Eingabe-Raster der Transmissivität der Formation: transm
Ausgabe-Richtungs-Raster: dir1
Ausgabe-Magnituden-Raster: mag1
Referenzen
Bear, J. Hydraulics of Groundwater. McGraw-Hill. 1979
Blatt, H., G. Middleton, and R. Murray Origin of Sedimentary Rocks, 2nd Ed. Prentice-Hall. 1980
Freeze, R. A., and J. A. Cherry. Grundwasser Prentice-Hall. 1979
Gelhar, L. W., C. Welty, and K. R. Rehfeldt. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research, 28 no. 7: 1955–1974. 1992.
Konikow, L. F. and J. D. Bredehoeft. "Computer Model of Two-Dimensional Solute Transport and Dispersion in Ground Water", USGS Techniques of Water Resources Investigations, Book 7, Chap. C2, U.S. Geological Survey, Washington, D.C. 1978.
Marsily, G. de. Quantitative Hydrogeology. Academic Press. 1986.
Tauxe, J. D. "Porous Medium Advection-Dispersion Modeling in a Geographic Information System". Doctoral Dissertation in Civil Engineering. The University of Texas at Austin, 1994.