Mit der Spatial Analyst-Lizenz verfügbar.
Das Werkzeug Hauptkomponenten wird verwendet, um die Daten in den Eingabe-Bändern vom eingegebenen multivariaten Attributraum in einen neuen multivariaten Attributraum umzuwandeln, dessen Achsen in Bezug auf den ursprünglichen Raum gedreht werden. Die Achsen (Attribute) im neuen Raum sind nicht korreliert. Der Hauptgrund für die Umwandlung der Daten in eine Hauptkomponentenanalyse ist, die Daten durch das Entfernen von Redundanzen zu komprimieren.
Ein Beispiel für Datenredundanz wird in einem Multiband-Raster offensichtlich, das Höhe, Neigung und Ausrichtung (auf einer kontinuierlichen Skala) umfasst. Da Neigung und Ausrichtung normalerweise von der Höhe abgeleitet werden, kann die Varianz innerhalb des Untersuchungsgebiets hauptsächlich allein durch die Höhe erklärt werden.
Das Ergebnis des Werkzeugs ist ein Multiband-Raster mit der gleichen Anzahl von Bändern wie die angegebene Anzahl von Komponenten (ein Band pro Achse oder Komponente im neuen multivariaten Raum). Die erste Hauptkomponente verfügt über die größte Varianz, die zweite zeigt die zweitgrößte, von der ersten nicht beschriebene Varianz an usw. Oft beschreiben die ersten drei oder vier Raster des aus dem Werkzeug Hauptkomponenten resultierenden Multiband-Rasters mehr als 95 Prozent der Varianz. Die verbleibenden einzelnen Raster-Bänder können entfernt werden. Da das neue Multiband-Raster weniger Bänder enthält und mehr als 95 Prozent der Varianz des ursprünglichen Multiband-Rasters intakt sind, sind die Berechnungen schneller und die Genauigkeit bleibt erhalten.
Für Hauptkomponenten müssen die Eingabebänder, die Anzahl der Hauptkomponenten, in die die Daten umgewandelt werden, der Name der Statistikausgabedatei und der Name des Ausgabe-Rasters identifiziert werden. Das Ausgabe-Raster enthält die gleiche Anzahl von Bändern wie die angegebene Anzahl von Komponenten. Jedes Band stellt eine Komponente dar.
Konzepte der Hauptkomponentenanalyse
Im Grunde wird anhand eines Zwei-Bänder-Rasters das Verschieben und Drehen der Achsen und die Umwandlung der Daten wie folgt erreicht:
- Die Daten werden in einem Scatterplot geplottet.
- Eine Ellipse wird berechnet, um die Punkte im Scatterplot einzuschließen (siehe Abbildung unten).
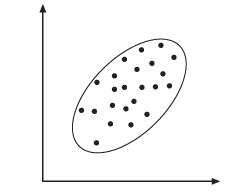
Grenze der geplotteten Ellipse - Die Hauptachse der Ellipse wird bestimmt (siehe Abbildung unten). Die Hauptachse wird zur neuen X-Achse, der ersten Hauptkomponente (PC1). PC1 stellt die größte Variation dar, da sie das größte Profil ist, das durch die Ellipse gezeichnet werden kann. Die Richtung von PC1 ist der Eigenvektor und ihr Betrag ist der Eigenwert. Der Winkel der X-Achse zu PC1 ist der Rotationswinkel, der bei der Transformation verwendet wird.
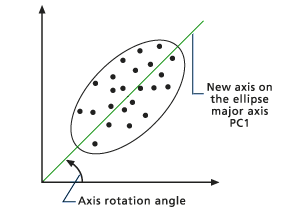
Erste Hauptkomponente - Es wird eine zu PC1 senkrechte orthogonale Linie berechnet. Diese Linie ist die zweite Hauptkomponente (PC2) und die neue Achse für die ursprüngliche Y-Achse (siehe Abbildung unten). Die neue Achse beschreibt die größte, von PC1 nicht beschriebene Varianz.
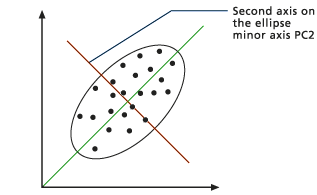
Zweite Hauptkomponente
Mit den Eigenvektoren, den Eigenwerten und der berechneten Kovarianzmatrix der Eingabe des Multiband-Rasters wird eine lineare Formel erstellt, welche die Verschiebung und Rotation definiert. Diese Formel wird angewendet, um jeden Zellenwert relativ zur neuen Achse zu transformieren.
Beispiel
Folgendes ist ein Beispiel der für drei Hauptkomponenten erstellten Ausgabedaten-Datei:
COVARIANCE MATRIX # Layer 1 2 3 # ----------------------------------------------------------- 1 34.1763 31.2377 51.8100 2 31.2377 212.6159 99.9540 3 51.8100 99.9540 118.8057 # =========================================================== # CORRELATION MATRIX # Layer 1 2 3 # ----------------------------------------------------------- 1 1.0000 0.3665 0.8131 2 0.3665 1.0000 0.6289 3 0.8131 0.6289 1.0000 # =========================================================== # EIGENVALUES AND EIGENVECTORS # Number of Input Layers Number of Principal Component Layers 3 3 # PC Layer 1 2 3 # ----------------------------------------------------------- # Eigen Values 287.8278 69.8781 7.8920 # Eigen Vectors # Input Layer 1 0.2112 0.4718 0.8560 2 0.8116 -0.5727 0.1154 3 0.5447 0.6704 -0.5039 # ===========================================================
Referenzliste
Campbell, James B. Introduction to Remote Sensing. The Guilford Press. 1987.
Jensen, John R. Introductory Digital Image Processing: A Remote Sensing Perspective. Prentice–Hall. 1986.
Lillesand, Thomas M. und Ralph W. Kiefer. Remote Sensing and Image Processing. John Wiley and Sons. 1987.
Richards, John A. Remote Sensing Digital Image Analysis: An Introduction. Berlin: Springer-Verlag. 1986.