Im Folgenden sehen Sie die verfügbaren Verteilungen für eine Reihe von Werkzeugen, mit denen Zufallswerte erzeugt werden. Mit den Verteilungen werden die 0–1-Zufallswerte, die aus dem angegebenen Stream (entweder global in der Analyseumgebung identifiziert oder lokal in Bezug auf das Werkzeug) erstellt werden, in die angegebene Verteilung transformiert. Die Syntax und Parameter für die jeweilige Verteilung finden Sie unter Die Verteilungssyntax für Zufallswerte.
Gleichverteilung
Gleichverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, bei der alle Werte innerhalb eines festgelegten Intervalls gleich wahrscheinlich sind. Eine ganzzahlige Verteilung ist eine diskontinuierliche Version der Gleichverteilung (siehe unten). Die Gleichverteilung kann beim Modellieren von Konzentrationen eines Gases in einem Simulationsmodell oder der Zeit zwischen Unfällen an einer Kreuzung sowie zum Platzieren der Punkte im Werkzeug Zufällige Punkte erstellen zum Einsatz kommen.
Gleichverteilung wird oftmals zum Modellieren von zufälligen Ereignissen verwendet, wenn das Eintreten jedes potenziellen Ergebnisses oder Vorfalls gleich wahrscheinlich ist.
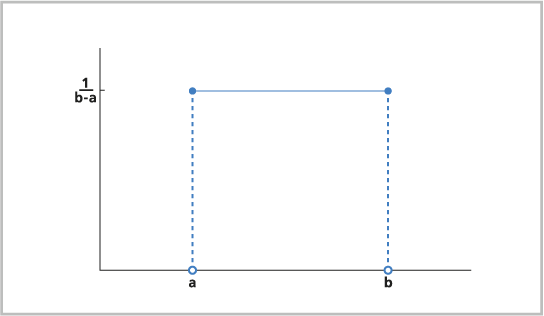
Die Gleichverteilungsformel lautet wie folgt:

wobei
a der Minimalwert des Intervalls mit gleicher Wahrscheinlichkeit ist.
b der Maximalwert des Intervalls mit gleicher Wahrscheinlichkeit ist.
x die Beobachtungen sind.
Die ausgewählten Zufallswerte liegen innerhalb des Bereichs zwischen Minimum und Maximum. Das Minimum muss geringer sein als das Maximum. Wenn kein Minimum und kein Maximum angegeben wird, werden einheitliche Variablen zwischen 0,0 und 1,0 erstellt.
Ganzzahlige Verteilung
Ganzzahlige Verteilung ist eine Wahrscheinlichkeitsverteilung, bei der alle diskontinuierlichen Werte innerhalb eines festgelegten Intervalls gleich wahrscheinlich sind. Ganzzahlige Verteilung ist die diskontinuierliche Version der Gleichverteilung (siehe oben). Ganzzahlige Verteilung kann zum Modellieren der Wahrscheinlichkeit des Auftretens jeder Zahl beim Werfen eines Würfels (die Auftretenswahrscheinlichkeit jeder Zahl liegt bei einem Sechstel), zum Modellieren von Zufallsereignissen in einem Simulationsmodell oder zum Auswählen von Stichprobenpositionen für eine biologische Studie verwendet werden.
Ganzzahlige Verteilung wird oftmals zum Modellieren von zufälligen Ereignissen verwendet, wenn das Eintreten jedes potenziellen Ergebnisses oder Vorfalls gleich wahrscheinlich ist.
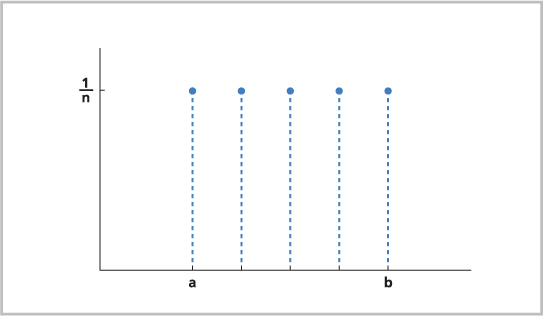
Im Folgenden sehen Sie die Formel der ganzzahligen Verteilung:
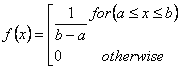
wobei
a der Minimalwert des Intervalls mit gleicher Wahrscheinlichkeit ist.
b der Maximalwert des Intervalls mit gleicher Wahrscheinlichkeit ist.
x die Beobachtungen sind.
Die ausgewählten Zufallswerte liegen innerhalb des Bereichs zwischen Minimum und Maximum. Das Minimum muss geringer sein als das Maximum. Wenn kein Minimum und kein Maximum angegeben wird, werden einheitliche Werte zwischen 1 und 100 erstellt.
Normalverteilung
Mit der Normalverteilung werden kontinuierliche Zufallswerte modelliert, die häufig auftreten. Die Verwendung der Normalverteilung ist weit verbreitet und trifft auf viele Anwendungen zu. Sie basiert auf dem zentralen Grenzwertsatz, der wiederum auf dem Grundsatz basiert, dass die Summe der Zufallsvariablen normal verteilt wird, wenn es eine große Zahl an Beobachtungen gibt. Beispielsweise kommt die Anzahl der Male, in der der Kopf in einer Folge von Münzwürfen erscheint, der Normalität nahe, wenn die Münze viele Male geworfen wird. Beispiele für Normalverteilungen sind die Größe der Menschen in einem Land, die Höhenwerte in einem US-Bundesstaat und die Mathematikprüfungsergebnisse aller 12-jährigen Schüler.
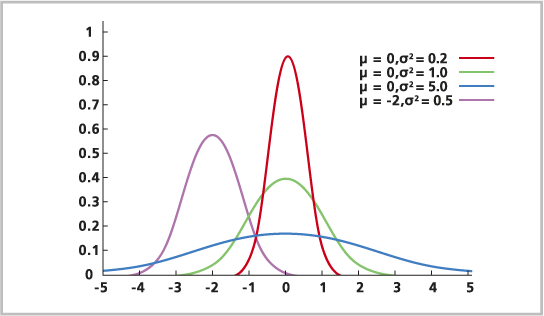
Die Formel der Normalverteilung lautet wie folgt:
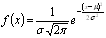
wobei
μ der Mittelwert ist.
σ die Standardabweichung ist (eine positive Zahl).
Normalverteilung ist symmetrisch relativ zum Mittelwert, Modus und Medianwert, die alle bei μ gleich sind.
Oftmals werden mit Binomial- und Poisson-Verteilungen zukünftige diskontinuierliche, unabhängige, zufällige, wahre oder falsche Ereignisse (z. B. die Anzahl der Male, in der der Kopf bei Münzwürfen erscheint) mithilfe einer relativ geringen Anzahl an Beobachtungen modelliert, während mit Normalverteilungen kontinuierliche Variablen (z. B. Größe, Gewicht und Menge) mithilfe einer großen Anzahl an Beobachtungen modelliert werden. Binomial- und Poisson-Verteilungen basieren auf der Wahrscheinlichkeit, während die Normalverteilung die Anzahl der Beobachtungen ist, die der Menge oder der Magnitude entspricht.
Exponentialverteilung
Exponentialverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Sie kommt generell zum Modellieren der Zeit zwischen Ereignissen zum Einsatz, die mit einer konstanten durchschnittlichen Rate auftreten. Alternativ kann die Verteilung verwendet werden, um das Auftreten von Ereignissen in einem bestimmten Abstand zu modellieren. Die Zeit bis zum nächsten Autounfall an einer Kreuzung, die Zeit zwischen zwei Sternschnuppen am Nachthimmel und die Entfernung zwischen Schlaglöchern in einer Straße sind allesamt Beispiele für Verwendungsmöglichkeiten der Exponentialverteilung. Bei jedem dieser Beispiele wächst mit zunehmender Zeit oder Entfernung die Wahrscheinlichkeit exponentiell, dass sich ein US-Bundesstaat ändert oder dass ein Ereignis eintritt. Die Ereignisse treten unabhängig voneinander ein.
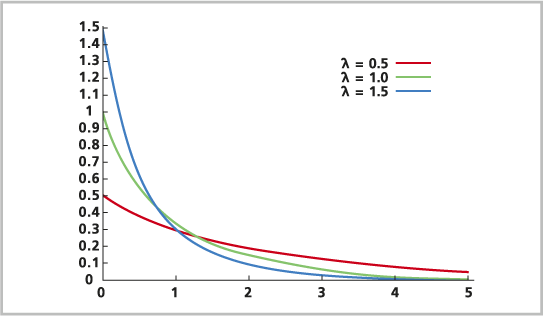
Die Formel der Exponentialverteilung lautet wie folgt:
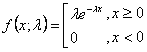
wobei
e der natürliche Logarithmus ist.
x die mögliche Anzahl des Eintretens des Ereignisses ist (positive ganzzahlige Werte).
Mit der Exponentialverteilung werden Poisson-Prozesse modelliert, bei denen sich das Phänomen im Anfangsstadium befindet. Exponentialverteilung ist die kontinuierliche Version der geometrischen Verteilung. Wenn der Prozess der Bewegung von Staat A zu Staat B in mehrere unabhängige Aufgaben unterteilt werden kann, ist es ggf. besser, ihn mit der Gamma-Verteilung zu modellieren. Mit der Gamma-Verteilung wird die Summe mehrerer unabhängiger exponenziell verteilter Variablen modelliert. Sie kann als spezieller Fall der Exponential-Verteilung betrachtet werden.
Poisson-Verteilung
Die Poisson-Verteilung ist eine Verteilung mit diskontinuierlicher Wahrscheinlichkeit. Mit der Poisson-Verteilung wird die Wahrscheinlichkeit der Anzahl von Ereignissen modelliert, die über einen festen Zeitschritt bei einem bekannten Mittelwert auftreten. Die Ereignisse sind unabhängig davon, wann sie zuletzt aufgetreten sind. Auf der X-Achse befinden sich die diskontinuierlichen Werte für die Ereignisse 0, 1, 2, 3, 4 usw. (die oftmals für die Anzahl der Male stehen, die das Ereignis auftritt), und auf der Y-Achse befindet sich die Wahrscheinlichkeit, dass das Phänomen bei einem bekannten Mittelwert so viele Male auftritt. Bei den Ereignissen kann es sich um die Anzahl von Unfällen an einer Kreuzung, die Anzahl an Geburtsfehlern oder die Anzahl von Elchen auf einem Quadratkilometer handeln. Mit der Poisson-Verteilung werden seltene Ereignisse modelliert. Die Verteilung wird zuweilen als das Gesetz der kleinen Zahlen bezeichnet, da das Ereignis nicht oft eintritt, es jedoch viele Gelegenheiten dafür gibt, dass es eintritt.
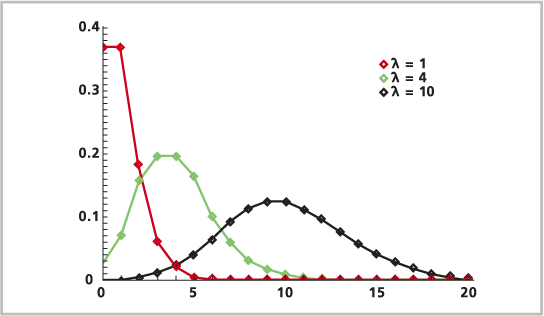
Die Formel ist im Folgenden dargestellt:
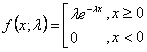
wobei
e der natürliche Logarithmus ist.
k die mögliche Anzahl des Eintretens des Ereignisses ist (positive ganzzahlige Werte).
k! ist eine Fakultät von k.
λ (oder der Mittelwert) ist eine positive Zahl, die für die erwartete Anzahl von Ereignissen innerhalb eines angegebenen Intervalls steht. Wenn das Ereignis alle 10 Minuten in einer Stunde (60 Minuten) eintritt, ist der Lambda-Wert 6.
Die Poisson-Verteilung ist ähnlich der Binomial-Verteilung. Bei der Poisson-Verteilung wird jedoch das Eintreten eines seltenen Ereignisses modelliert, ohne dass etwas über die Gesamtzahl der möglichen Ereignisse bekannt ist. Mit der Poisson-Verteilung wird die Anzahl der Unfälle an einer Kreuzung untersucht, während mit der Binomial-Verteilung die Anzahl der Unfälle relativ zur Anzahl der Autos modelliert wird, die die Kreuzung passieren.
Gamma-Verteilung
Die Gamma-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Mit der Gamma-Verteilung wird die Summe mehrerer unabhängiger exponenziell verteilter Variablen modelliert. Sie kann als spezieller Fall der Exponential-Verteilung betrachtet werden.

Die Formel der Gamma-Verteilung lautet wie folgt:
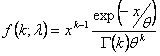
Eine weitere Möglichkeit der Parametrisierung der Gamma-Verteilung sehen Sie hier:

Bei einem Alpha-Wert von 1 enspreicht die Gamma-Verteilung der Exponential-Verteilung. Wenn der Alpha-Wert eine Ganzzahl ist, wird die Gamma-Verteilung zur Erlang-Verteilung. Bei einem ganzzahligen Alpha-Wert und einem Beta-Wert von 2 wird die Gamma-Verteilung zu einer Chi-Quadrat-Verteilung mit 2 Alpha-Freiheitsgraden.
Die resultierenden Variablen sind größer als oder gleich 0,0. Der Alpha- und der Beta-Wert müssen größer sein als 0,0.
Binomial-Verteilung
Mit der Binomial-Verteilung wird die Anzahl modelliert, in der ein Ereignis eintritt, während eine Folge potenzieller Verursacher des Ereignisses beobachtet wird. Mit der Binomial-Verteilung wird beispielsweise die Anzahl der Personen in einer klinischen Studie erfasst, die an einer Herzkrankheit gestorben sind, die Anzahl der Personen, die im zweiten Stock aus einem überfüllten Fahrstuhl aussteigen oder die Anzahl an Tieren in einer Population, die einen bestimmten genetischen Wesenszug haben.

Die Binomial-Verteilung beschreibt das Eintreten von Ereignissen, nicht die Magnitude. Mit ihr lässt sich modellieren, wie viele Teilnehmer ein Rennen beendet haben und nicht, wie schnell die Teilnehmer waren.
Die Formel der Binomial-Verteilung lautet wie folgt:
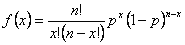
wobei
n die Anzahl der Beobachtungen ist.
p die Eintretenswahrscheinlichkeit ist.
x die Anzahl der Erfolge zwischen 0 und n ist.
Häufig wird die Binomial-Verteilung beispielsweise zum Ermitteln der Wahrscheinlichkeit der Häufigkeit eingesetzt, mit der der Kopf erscheint, wenn eine Münze zehnmal geworfen wird (n = 10). Der Kopf kann 0-mal von 10 erscheinen, 1-mal von 10 usw. Daher ist x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Und p ist die Wahrscheinlichkeit für jedes x.
Alle Versuche sind unabhängig, und jeder Versuch hat als Ergebnis Erfolg oder Misserfolg.
Die Binomial-Verteilung nähert sich bei einem großen n-Wert und einem kleinen p-Wert der Poisson-Verteilung an. In diesem Fall ist es ggf. leichter, die Poisson-Verteilung zu verwenden.
Bei der Binomial-Verteilung wird eine zufällige Variable für die Anzahl der Erfolge aus n Versuchen zurückgegeben, wobei die Wahrscheinlichkeit eines Erfolgs in jedem Versuch p ist (z. B. ist die Wahrscheinlichkeit, dass der Kopf oben ist, gleich p).
Geometrische Verteilung
Die geometrische Verteilung ist eine Verteilung mit diskontinuierlicher Wahrscheinlichkeit. Es gibt zwei Haupttypen von Phänomenen, die mit ihr modelliert werden: (1) die Wahrscheinlichkeit der Anzahl der Male, die es bis zu einem Erfolg dauert (z. B. die Anzahl der Würfe eines Würfels, bevor das Ergebnis eine 6 ist) oder (2) die Wahrscheinlichkeit der Anzahl an Misserfolgen, bevor ein Erfolg eintritt (z. B. die Anzahl an Wanderungen, die es braucht, bevor man ein Reh sieht). Die Wahrscheinlichkeit, mit der man auf seiner ersten Wanderung kein Reh sieht ist (1 - p). Bei der zweiten Wanderung beträgt die Wahrscheinlichkeit, kein Reh zu sehen (1 - p) (1 - p). Bei zunehmender Anzahl an Wanderungen nimmt die Wahrscheinlichkeit, kein Reh zu sehen, exponenziell ab, und schließlich wird ein Reh gesichtet. Die Ereignisse sind unabhängig von einander.

Die Formel der geometrischen Verteilung lautet wie folgt:

wobei
p die Erfolgswahrscheinlichkeit ist.
n die Anzahl der Versuche ist.
Die geometrische Verteilung ist die diskontinuierliche Version der Exponential-Verteilung (siehe oben). Die geometrische Verteilung ist ein spezieller Fall der negativen Binomial- oder Pascal-Verteilung, wobei r in der Pascal-Verteilung gleich 1 ist (siehe unten).
Negative Binomial-Verteilung
Die negative Binomial-Verteilung ist eine diskontinuierliche Wahrscheinlichkeitsverteilung. Die negative Binomial-Verteilung basiert auf Bernoulli-Versuchen. Mit Bernoulli-Versuchen werden Ereignisse modelliert, bei denen Versuche eines von zwei Ergebnissen haben (Erfolg und Misserfolg). Sie haben eine Erfolgswahrscheinlichkeit p (wobei p in jedem Versuch dasselbe ist) und sind unabhängig voneinander. Das Werfen einer Münze ist ein Bernoulli-Versuch. Mit einer negativen Binomial-Verteilung lässt sich beispielsweise modellieren, wie viele Würfe einer Münze es braucht, bis der Kopf fünfmal hintereinander erscheint. Somit wird mit der negativen Binomial-Verteilung die Anzahl der Misserfolge vor einem Erfolg modelliert. Wenn r eine Ganzzahl ist, wird die negative Binomial-Verteilung zu einem speziellen Fall, der Pascal-Verteilung genannt wird.
Die Formel der negativen Binomial-Verteilung lautet wie folgt:
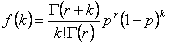
wobei
r die Anzahl der Misserfolge ist.
p die Erfolgswahrscheinlichkeit ist.
k die Anzahl der Erfolge zwischen 0 und n ist.
Wenn die negative Binomial-Verteilung durch das Werfen einer Münze dargestellt wird, wird für die Anzahl der Male, die es dauert, bis der Kopf erscheint ein zufälliger Wert zurückgegeben.