Mit der Geostatistical Analyst-Lizenz verfügbar.
Disjunctive Kriging erfordert, dass die Daten aus einer bivariaten Normalverteilung stammen. Außerdem wird beim Erstellen von Wahrscheinlichkeits- und Quantilkarten davon ausgegangen, dass die Daten aus einer vollständigen multivariaten Normalverteilung stammen. Sie können mit dem Histogramm prüfen, ob eine univariate Normalverteilung vorliegt (zwar ist hierdurch nicht garantiert, dass die Daten aus einer vollständigen multivariaten Normalverteilung stammen, aber es ist häufig plausibel, dies anzunehmen, wenn univariate Normalverteilungen mit diesem Diagramm erkannt werden).
Beachten Sie die folgende Wahrscheinlichkeitsaussage:
f(p,h) = Prob[Z(s) ≤ zp, Z(s + h) ≤ zp]Dabei gilt: zp ist das Standard-Normal-Quantil für die Wahrscheinlichkeit p.
Ein bekanntes Standard-Normal-Quantil liegt beispielsweise vor, wenn p = 0,975, dann ist zp = 1,96, wenn p = 0,5, dann ist zp = 0, und wenn p = 0,025, dann ist zp = -1,96. Die obige Wahrscheinlichkeitsaussage verwendet eine Variable Z an der Position s und eine andere Variable Z an einer anderen Position s + h und geht von der Wahrscheinlichkeit aus, dass beide kleiner sind als zp. Diese Wahrscheinlichkeitsaussage ist eine Funktion f(p,h), die von p (und folglich von zp) und h abhängig ist. Außerdem ist die Funktion von der Höhe der Autokorrelation zwischen Z(s) und Z(s + h) abhängig.
Angenommen, Z(s) und Z(s + h) weisen eine bivariate Normalverteilung auf. Wenn die Autokorrelation bekannt ist, gibt es Formeln für f(p,h). Wenn wir weiterhin annehmen, dass h konstant ist und nur p sich ändert, wäre eine Funktion wie die folgende zu erwarten:
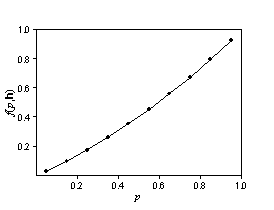
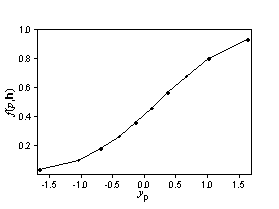
Die zweite Abbildung zeigt eine kumulative Wahrscheinlichkeitsverteilung. Nehmen wir nun an, dass p konstant ist und f(p,h) sich mit h ändert.
Zunächst gehen wir davon aus, dass h sehr klein ist. In diesem Fall ist Prob[Z(s) ≤ zp, Z(s + h) ≤ zp] nahezu identisch mit Prob[Z(s) ≤ zp] = p. Nun gehen wir davon aus, dass h sehr groß ist. In diesem Fall ist Prob[Z(s) ≤ zp, Z(s + h) ≤ zp] nahezu identisch mit Prob[Z(s) ≤ zp] Prob[Z(s + h) ≤ zp] = p2 (weil Z(s) und Z(s + h) praktisch unabhängig voneinander sind). Wenn p konstant ist, können Sie also davon ausgehen, dass f(p,h) zwischen p und p2 variiert. Wenn Sie nun f(p,h) als Funktion von p und der Länge von h betrachten, könnten Sie etwas Ähnliches wie in der folgenden Abbildung beobachten:
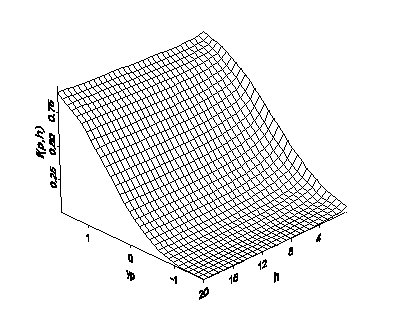
Diese Funktion kann in Semivariogramme und Kovarianzfunktionen für Indikatoren konvertiert werden. Unter der Berücksichtigung, dass Prob[Z(s) ≤ zp, Z(s + h) ≤ zp] = E[I(Z(s) ≤ zp)xI(Z(s + h) ≤ zp)] – wobei I(Aussage) die Indikatorfunktion ist – 1 ist, wenn Aussage wahr ist, und andernfalls 0 ist, lautet die Kovarianzfunktion für die Indikatoren für einen konstanten Wert von p wie folgt:
CI(h;p) = f(p,h) –p2,und die Semivariogramm-Formel für die Indikatoren für einen konstanten Wert von p wie folgt:
γI(h;p) = p - f(p,h).Somit können Sie die Semivariogramm- und Kovarianzfunkion für die Indikatoren der ursprünglichen Daten schätzen und diese verwenden, um die erwarteten Semivariogramme und Kovarianzfunktionen der Indikatoren für verschiedene Werte von p zu erhalten.
Weitere Informationen zu Semivariogrammen und Kovarianzfunktionen