Mit der Geostatistical Analyst-Lizenz verfügbar.
Bei der inversen distanzgewichteten (IDW-)Interpolation wird ausdrücklich davon ausgegangen, dass Dinge, die nahe beieinander liegen, einander ähnlicher sind als solche, die weiter auseinander liegen. Um den Wert für eine ungemessene Position vorherzusagen, verwendet IDW die gemessenen Werte, die die vorhergesagte Position umgeben. Die Messwerte, die am nächsten an der vorhergesagten Position liegen, haben mehr Einfluss auf den vorhergesagten Wert als diejenigen, die weiter entfernt sind. Bei der IDW wird angenommen, dass jeder gemessene Punkt einen lokalen Einfluss hat, der mit zunehmender Entfernung abnimmt. Die Punkte, die am nächsten an der vorhergesagten Position liegen, erhalten eine größere Gewichtung, und die Gewichtungen nehmen als Funktion der Entfernung oder Distanz ab. Daher der Name inverse Distanzgewichtung. Im folgenden Beispiel sind die Gewichtungen dargestellt, die Datenpunkten zugewiesen sind:
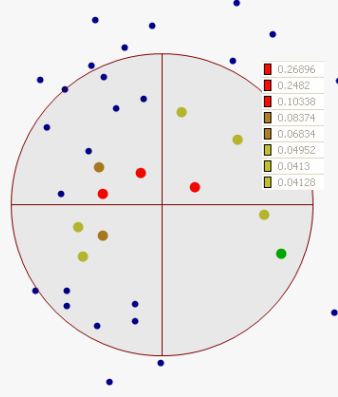
Das Fenster "Gewichtungen" enthält die Liste der Gewichtungen, die jedem Datenpunkt zugewiesen sind, mit dem an der durch das Fadenkreuz gekennzeichneten Position ein vorhergesagter Wert generiert wird.
Weitere Informationen zu den in ArcGIS Geostatistical Analyst verfügbaren Interpolationsmethoden
Die Potenzfunktion
Wie oben erwähnt, sind Gewichtungen proportional zum inversen Wert der Distanz (zwischen dem Datenpunkt und der vorhergesagten Position) potenziert mit dem Potenzwert p. Folglich nimmt die Gewichtung mit zunehmender Entfernung schnell ab. Wie schnell die Gewichtungen abnehmen, hängt vom Wert p ab. Wenn p = 0 ist, nimmt der Wert mit zunehmender Entfernung nicht ab, und da jede Gewichtung λi gleich ist, entspricht die Vorhersage dem Mittelwert aller Datenwerte in der Suchnachbarschaft. Wenn p zunimmt, nehmen die Gewichtungen für entfernte Punkte schnell ab. Ist der Wert p sehr hoch, wird die Vorhersage lediglich durch die unmittelbar umgebenden Punkte beeinflusst.
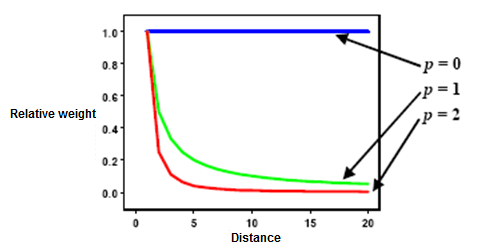
Geostatistical Analyst verwendet Potenzwerte von größer oder gleich 1. Wenn p = 2 ist, wird die Methode als gewichtete Interpolation nach inverser Entfernung im Quadrat bezeichnet. Der Standardwert ist p = 2, obwohl es theoretisch keine Rechtfertigung dafür gibt, diesen Wert anderen Werten vorzuziehen. Die Auswirkung, die eine Änderung von p mit sich bringt, sollte untersucht werden, indem eine Vorschau der Ausgabe erstellt und die Kreuzvalidierungsstatistik geprüft wird.
Die Suchnachbarschaft
Da Dinge, die nahe beieinander liegen, sich ähnlicher sind, als solche, die weiter voneinander entfernt sind, haben die Messwerte mit zunehmender Entfernung der Positionen eine geringere Beziehung zu dem Wert der vorhergesagten Position. Um die Berechnungen zu beschleunigen, können Sie die weiter entfernten Punkte, die wenig Einfluss auf die Vorhersage haben, ausschließen. Folglich ist es gängige Praxis, die Anzahl der Messwerte durch Angabe einer Suchnachbarschaft zu begrenzen. Durch die Form der Nachbarschaft werden die Reichweite und die Positionen, an denen nach den in der Vorhersage zu verwendenden Messwerten gesucht werden soll, eingeschränkt. Andere Nachbarschaftsparameter schränken die Positionen ein, die innerhalb dieser Form verwendet werden. In dem folgenden Bild werden zur Vorhersage eines Wertes für die Position ohne Messwert, den gelben Punkt, fünf Messpunkte (Nachbarn) verwendet.
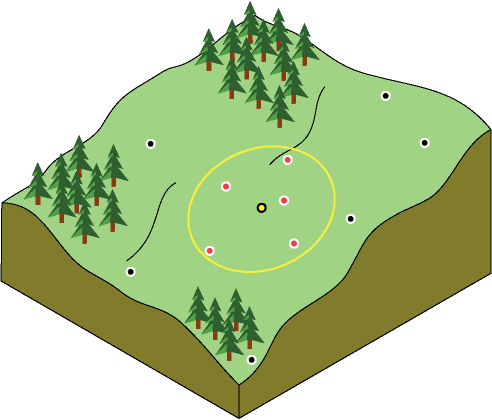
Die Form der Nachbarschaft wird durch die Eingabedaten und die Oberfläche beeinflusst, die Sie zu erstellen versuchen. Falls es in Ihren Daten keine Richtungseinflüsse gibt, können Sie Punkte gleichermaßen in allen Richtungen berücksichtigen. Definieren Sie hierzu die Suchnachbarschaft als Kreis. Falls es in Ihren Daten jedoch einen Richtungseinfluss gibt, wie z. B. eine vorherrschende Windrichtung, können Sie sie ausgleichen, indem Sie die Form der Suchnachbarschaft in eine Ellipse mit der Hauptachse parallel zum Wind ändern. Der Ausgleich für diesen Richtungseinfluss ist gerechtfertigt, da Sie wissen, dass sich Positionen, die sich auf der Windseite der vorhergesagten Position befinden, in größeren Entfernungen ähnlicher sind als Positionen, die sich rechtwinklig zum Wind, aber näher an der vorhergesagten Position befinden.
Nachdem Sie die Form der Nachbarschaft festgelegt haben, können Sie einschränken, welche Datenpositionen innerhalb der Form verwendet werden sollen. Sie können definieren, wie viele Positionen höchsten uns mindestens verwendet werden, und Sie können die Nachbarschaft in Sektoren unterteilen. Wenn Sie die Nachbarschaft in Sektoren unterteilen, werden die Höchst- und Mindestwerteinschränkungen auf alle Sektoren angewendet.
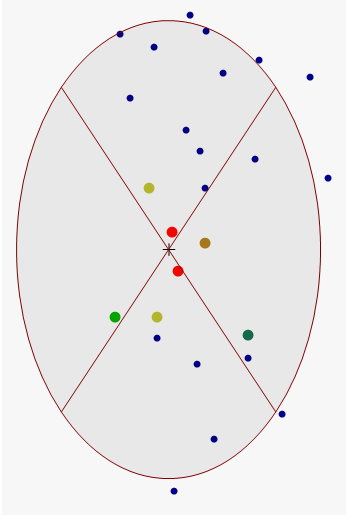
Die in der Datenansicht hervorgehobenen Punkte zeigen die Positionen und die Gewichtungen, die zur Vorhersage einer Position im Mittelpunkt der Ellipse (an der Position des Fadenkreuzes) verwendet werden. Die Suchnachbarschaft ist auf das Innere der Ellipse begrenzt. In dem nachfolgenden Beispiel erhalten die beiden roten Punkte Gewichtungen von mehr als 10 Prozent. Im östlichen Sektor erhält ein Punkt (braun) eine Gewichtung zwischen 5 Prozent und 10 Prozent. Die restlichen Punkte in der Suchnachbarschaft erhalten geringere Gewichtungen.
Wann IDW verwendet wird
Eine per IDW berechnete Oberfläche ist von der Auswahl des Potenzwertes (p) und der Strategie der Suchnachbarschaft abhängig. Die IDW ist ein exakter Interpolator, bei dem die Höchst- und Mindestwerte (siehe das nachfolgende Diagramm) auf der interpolierten Oberfläche nur an Referenzpunkten auftreten können.

Die Ausgabe-Oberfläche reagiert auf Cluster-Bildung und Ausreißer. Bei der IDW wird davon ausgegangen, dass das modellierte Phänomen auf lokaler Variation beruht, die erfasst (modelliert) werden kann, indem eine angemessene Suchnachbarschaft definiert wird. Da es bei der IDW keine Standardfehler der Vorhersage gibt, kann es problematisch sein, den Einsatz dieses Modells zu rechtfertigen.