Die Regressionsanalyse ist die wohl am häufigsten verwendete Statistik in den Sozialwissenschaften. Regression wird zur Auswertung von Beziehungen zwischen zwei oder mehreren Feature-Attributen verwendet. Durch die Identifizierung und Messung von Beziehungen können Sie besser verstehen, welche Ereignisse an einem Ort auftreten, vorhersagen, wo Ereignisse eintreten könnten, oder Ursachen für das Auftreten von Ereignissen an bestimmten Orten untersuchen.
Kleinste Quadrate (Ordinary Least Squares, OLS) ist die bekannteste Regressionstechnik. Sie ist auch ein Ausgangspunkt für alle räumlichen Regressionsanalysen. OLS bietet ein globales Modell der Variablen oder des Prozesses, die bzw. den Sie versuchen, zu verstehen oder vorherzusagen; es erstellt eine einzelne Regressionsgleichung zur Darstellung dieses Prozesses.
Es gibt zahlreiche Ressourcen, mit denen Sie mehr über die OLS-Regression und die geographisch gewichtete Regression erfahren können. Beginnen Sie mit Grundlagen zur Regressionsanalyse. Arbeiten Sie dann das Lernprogramm zur Regressionsanalyse durch. In diesem Thema werden die Ergebnisse der Analyse beschrieben, um Ihnen ein besseres Verständnis der Ausgabe und Diagnose von OLS zu vermitteln.
Eingaben
Geben Sie zum Ausführen des OLS-Werkzeugs eine Eingabe-Feature-Class mit einem eindeutigen ID-Feld, der zu modellierenden, zu erläuternden oder vorherzusagenden abhängigen Variablen und einer Liste mit erklärenden Variablen an. Sie müssen auch einen Pfad für die Ausgabe-Feature-Class und optional Pfade für die Ausgabeberichtsdatei, die Koeffizienten-Ausgabetabelle und die Diagnose-Ausgabetabelle angeben.
Interpretieren von OLS-Ergebnissen
Die vom OLS-Werkzeug generierte Ausgabe beinhaltet eine Ausgabe-Feature-Class, die mit den OLS-Residuen symbolisiert wird, statistische Ergebnisse und Diagnosen im Fenster Meldungen sowie mehrere optionale Ausgaben, z. B. eine PDF-Berichtsdatei, eine Tabelle erklärender Variablenkoeffizienten und eine Tabelle mit Regressionsdiagnosen. Jede dieser Ausgaben wird nachfolgend als eine Reihe von Prüfungen beim Ausführen der OLS-Regression und Interpretieren der OLS-Ergebnisse beschrieben.
Überprüfen Sie nach der Ausführung von OLS den OLS-Zusammenfassungsbericht, der während der Ausführung des Werkzeugs in Form von Meldungen verfügbar ist und in eine Berichtsdatei geschrieben wird, wenn Sie einen Pfad für den Parameter Ausgabeberichtsdatei angeben.
Sehen Sie sich den Übersichtsbericht mithilfe der unten aufgeführten Schritte an.
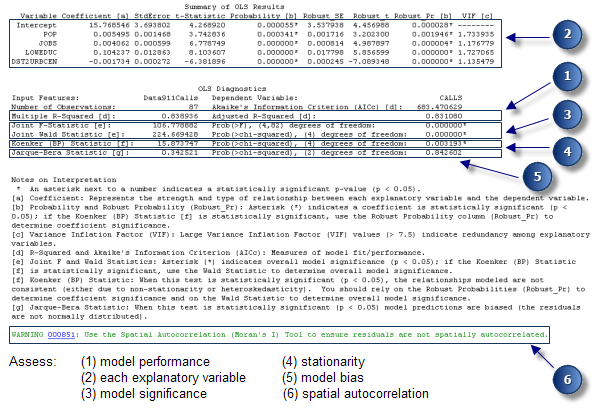
Bewerten des statistischen Berichts
- Bewerten Sie die Modell-Performance. Sowohl der Wert "Multiple R-Squared" als auch der Wert "Adjusted R-Squared" sind Messwerte für die Modell-Performance. Zulässige Werte können zwischen 0,0 und 1,0 liegen. Der Adjusted R-Squared-Wert ist immer etwas niedriger als der Multiple R-Squared-Wert, da er die Modellkomplexität (die Anzahl von Variablen) im Verhältnis zu den Daten widerspiegelt, und ist daher ein etwas genauerer Wert für die Modell-Performance. Durch Hinzufügen einer erklärenden Variablen zum Modell kann der Multiple R-Squared-Wert erhöht werden, der Adjusted R-Squared-Wert wird dabei jedoch reduziert. Angenommen, Sie erstellen ein Regressionsmodell für Wohnungseinbrüche (die Anzahl der Wohnungseinbrüche, die mit den einzelnen Zählbezirken verknüpft ist, ist die abhängige Variable, y). Ein Adjusted R-Squared-Wert von 0,39 würde darauf hinweisen, dass das Modell (die mithilfe der linearen Regression modellierten erklärenden Variablen) ca. 39 Prozent der Variation in der abhängigen Variable erklärt. Anders ausgedrückt: Das Modell gibt zu ca. 39 % Aufschluss über die Wohnungseinbrüche.

R-Squared-Werte quantifizieren die Modell-Performance. - Bewerten Sie die einzelnen erklärenden Variablen im Modell: Koeffizient, Wahrscheinlichkeit oder robuste Wahrscheinlichkeit und Varianzinflationsfaktor (VIF). Der Koeffizient für jede erklärende Variable spiegelt sowohl die Stärke als auch den Typ der Beziehung wider, die die erklärende Variable zu der abhängigen Variable hat. Wenn das dem Koeffizienten zugewiesene Zeichen negativ ist, ist die Beziehung negativ (je größer beispielsweise die Entfernung vom Stadtzentrum ist, desto kleiner ist die Anzahl der Wohnungseinbrüche). Wenn das Zeichen positiv ist, ist die Beziehung positiv (je größer beispielsweise die Bevölkerung ist, desto größer ist auch die Anzahl der Wohnungseinbrüche). Koeffizienten werden in denselben Einheiten wie ihre zugeordneten erklärenden Variablen angegeben (ein Koeffizient von 0,005, der einer Variablen zugeordnet ist, die die Bevölkerungszahl darstellt, kann als 0,005 Personen interpretiert werden). Der Koeffizient spiegelt die erwartete Änderung in der abhängigen Variable pro Einheitenänderung in der zugeordneten erklärenden Variable wider, wenn alle anderen Variablen konstant bleiben (für jede zusätzliche Person im Zählblock wird beispielsweise ein Anstieg von 0,005 bei den Wohnungseinbrüchen erwartet, alle anderen erklärenden Variablen bleiben konstant). Mithilfe des T-Tests können Sie beurteilen, ob eine erklärende Variable statistisch signifikant ist. Die Nullhypothese besagt, dass der Koeffizient für alle Zwecke gleich Null ist (und infolgedessen dem Modell nicht hilft). Wenn die Wahrscheinlichkeit oder die robuste Wahrscheinlichkeit (p-Wert) sehr niedrig ist, ist auch die Wahrscheinlichkeit, dass der Koeffizient tatsächlich Null ist, sehr gering. Wenn der Koenker-Test (siehe unten) statistisch signifikant ist, verwenden Sie die robusten Wahrscheinlichkeiten, um zu beurteilen, ob die erklärende Variable statistisch signifikant ist. Statistisch signifikante Wahrscheinlichkeiten sind mit einem Sternchen (*) gekennzeichnet. Eine erklärende Variable, die mit einem statistisch signifikanten Koeffizienten verknüpft ist, ist für das Regressionsmodell wichtig, wenn die Theorie bzw. der gesunde Menschenverstand eine gültige Beziehung mit der abhängigen Variable unterstützen, wenn die modellierte Beziehung in erster Linie linear ist und wenn die Variable nicht redundant zu anderen erklärenden Variablen im Modell ist. Mit dem VIF wird die Redundanz unter erklärenden Variablen gemessen. Als Faustregel gilt, dass mit VIF-Werten verknüpfte erklärende Variablen, die größer als 7,5 sind, aus dem Regressionsmodell (einzeln) entfernt werden müssen. Wenn Sie beispielsweise eine Bevölkerungsvariable (die Anzahl der Personen) und eine Beschäftigungsvariable (die Anzahl der angestellten Personen) im Regressionsmodell haben, sind diese mit großer Wahrscheinlichkeit mit großen VIF-Werten verknüpft, die angeben, dass beide Variablen dasselbe aussagen; eine der Variablen sollte daher aus dem Modell entfernt werden.
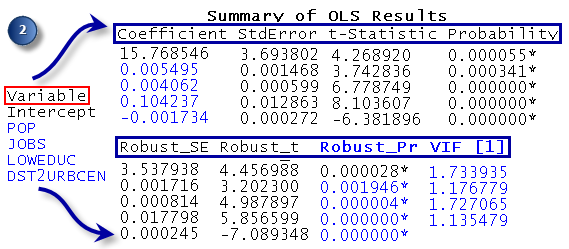
Beurteilen Sie, welche Variablen statistisch signifikant sind. - Bewerten Sie die Modellsignifikanz. Sowohl die Joint F-Statistik als auch die Joint Wald-Statistik sind Messwerte für die allgemeine statistische Signifikanz von Modellen. Die Joint F-Statistic ist nur vertrauenswürdig, wenn die Koenker-Statistik (BP-Statistik) (siehe unten) nicht statistisch signifikant ist. Wenn die Koenker-Statistik (BP-Statistik) signifikant ist, ziehen Sie die Joint Wald Statistic heran, um die allgemeine Modellsignifikanz zu ermitteln. Die Nullhypothese für beide Tests besagt, dass die erklärenden Variablen im Modell nicht wirksam sind. Ein Konfidenzniveau von 95 Prozent bedeutet, dass ein p-Wert (Wahrscheinlichkeit) kleiner als 0,05 für ein statistisch signifikantes Modell steht.
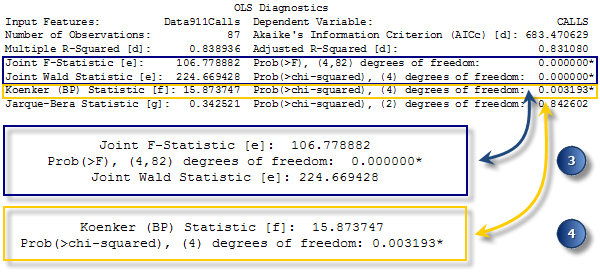
Bewerten Sie die allgemeine statistische Signifikanz des Regressionsmodells. - Bewerten Sie die Stationarität. Mit der Koenker-(BP)-Statistik (Koenkers t-verteilte Breusch-Pagan-Statistik) wird ermittelt, ob die erklärenden Variablen im Modell über eine konsistente Beziehung zur abhängigen Variable sowohl im geographischem Raum als auch im Datenbereich aufweisen. Wenn das Modell im geographischem Raum konsistent ist, verhalten sich die durch die erklärenden Variablen dargestellten räumlichen Prozesse genauso wie überall im Untersuchungsgebiet (die Prozesse sind stationär). Wenn das Modell im Datenbereich konsistent ist, ändert sich die Variation in der Beziehung zwischen vorhergesagten Werten und jeder erklärenden Variable nicht bei Änderungen der Beträge der erklärenden Variablen (es gibt keine Heteroskedastizität im Modell). Angenommen, Sie möchten Verbrechen vorhersagen, und eine der erklärenden Variablen ist das Einkommen. Das Modell würde eine problematische Heteroskedastizität aufweisen, wenn die Vorhersagen für Orte mit niedrigem mittleren Einkommen genauer wären als für Orte mit hohem mittleren Einkommen. Die NULL-Hypothese für diesen Test ist, dass das Modell stationär ist. Ein Konfidenzniveau von 95 Prozent bedeutet, dass ein p-Wert (Wahrscheinlichkeit) kleiner als 0,05 Heteroskedastizität und/oder Nichtstationarität angibt. Wenn die Ergebnisse dieses Tests statistisch signifikant sind, ziehen Sie die robusten Koeffizientenstandardfehler und Wahrscheinlichkeiten heran, um die Effektivität der einzelnen erklärenden Variablen zu bewerten. Regressionsmodelle mit statistisch signifikanter Nichtstationarität sind häufig gute Kandidaten für die GWR-Analyse Geographisch gewichtete Regression .
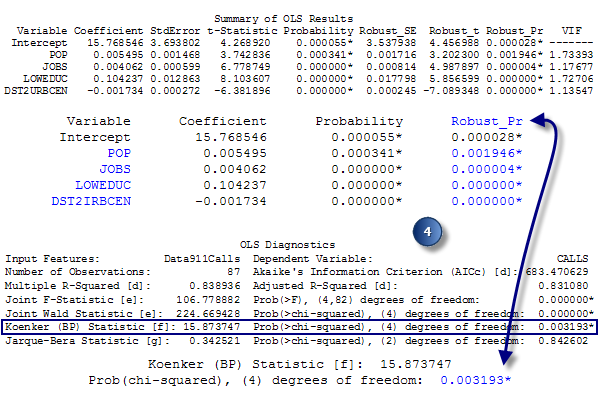
Bewerten Sie die Stationarität: Wenn der Koenker-Test statistisch signifikant (*) ist, ziehen Sie die robusten Wahrscheinlichkeiten heran, um zu beurteilen, ob die erklärenden Variablenkoeffizienten statistisch signifikant sind. - Bewerten Sie die Modelltendenz. Die Jarque-Bera-Statistik gibt an, ob die Residuen (die beobachteten oder bekannten abhängigen Variablenwerte abzüglich der vorhergesagten oder geschätzten Werte) normal verteilt sind. Die Nullhypothese für diesen Test besagt, dass die Residuen normal verteilt sind, wenn Sie also ein Histogramm für diese Residuen erstellen würden, würden diese eine klassische Glockenkurve bzw. eine Gauß'sche Verteilung darstellen. Wenn der p-Wert (Wahrscheinlichkeit) für diesen Test klein ist (z. B. kleiner als 0,05 für ein Konfidenzniveau von 95), werden die Residuen nicht normal verteilt, was auf ein verzerrtes Modell hinweist. Wenn zudem eine statistisch signifikante räumliche Autokorrelation Ihrer Residuen vorliegt (siehe unten), liegt die Ursache für die Verzerrung möglicherweise an einer falschen Angabe des Modells (eine wichtige Modellvariable fehlt). Ergebnisse aus einem falsch angegebenen OLS-Modell sind nicht vertrauenswürdig. Ein statistisch signifikanter Jarque-Bera-Test ist auch möglich, wenn Sie nicht lineare Beziehungen modellieren, wenn Ihre Daten einflussreiche Ausreißer enthalten oder wenn eine starke Heteroskedastizität vorliegt.
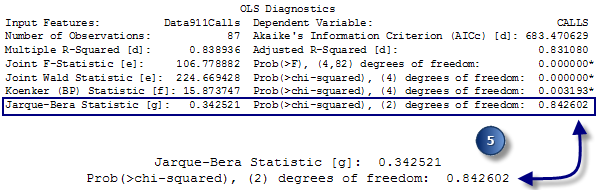
Bewerten Sie die Modelltendenz. - Bewerten Sie räumliche Autokorrelation von Residuen. Führen Sie immer das Werkzeug Räumliche Autokorrelation (Morans I) für die Regressionsresiduen aus, um sicherzustellen, dass sie räumlich zufällig sind. Die statistisch signifikante Cluster-Bildung von hohen und niedrigen Residuen (zu niedrige und zu hohe Vorhersagen für das Modell) deuten darauf hin, dass eine wichtige Variable in dem Modell fehlt (falsche Angabe). OLS-Ergebnisse sind nicht vertrauenswürdig, wenn das Modell falsch angegeben ist.

Stellen Sie mit dem Werkzeug für die räumliche Autokorrelation sicher, dass Modellresiduen nicht räumlich autokorreliert werden. - Überprüfen Sie anhand des Abschnitts Wie Regressionsmodelle ungültig werden des Dokuments Grundlagen zur Regressionsanalyse, ob Ihr OLS-Regressionsmodell korrekt angegeben ist. Wenn Sie kein ordnungsgemäß spezifiziertes Regressionsmodell finden können, kann das Werkzeug Regressionsanalyse hilfreich sein. Die Hinweise zur Interpretation am Ende des OLS-Zusammenfassungsberichts unterstützen Sie dabei, den Zweck der einzelnen statistischen Tests zu erkennen und eine Lösung zu finden, wenn Ihr Modell bei einer oder mehreren Diagnosen Fehler aufweist.

Der OLS-Bericht umfasst Hinweise, mit denen Sie die Diagnoseausgabe interpretieren können.
Wenn Sie einen Pfad für die optionale Ausgabeberichtsdatei angeben, wird eine PDF-Datei mit dem gesamten Inhalt des Übersichtsberichts plus weiterer Diagramme zur Bewertung des Modells erstellt. Die erste Seite des Berichts enthält Informationen zu den einzelnen erklärenden Variablen. Ähnlich wie beim ersten Abschnitt des Übersichtsberichts (siehe unter 2. weiter oben) verwenden Sie die hier aufgeführten Informationen um zu ermitteln, ob die Koeffizienten jeder erklärenden Variable statistisch signifikant sind und das erwartete Vorzeichen (+/-) aufweisen. Wenn der Koenker-Test statistisch signifikant ist (siehe unter 4. weiter oben), können Sie nur den robusten Wahrscheinlichkeiten vertrauen, um festzustellen, ob eine Variable für Ihr Modell hilfreich ist. Statistisch signifikante Koeffizienten sind durch ein Sternchen neben den p-Werten in den Spalten für die Wahrscheinlichkeiten und robusten Wahrscheinlichkeiten gekennzeichnet. Anhand der Informationen auf dieser Seite des Berichts können Sie auch ermitteln, ob erklärende Variablen möglicherweise redundant sind (eine problematische Multikollinearität aufweisen). Falls durch die Theorie nicht anders vorgegeben, sollten erklärende Variablen mit erhöhten Werten für den Varianzinflationsfaktor (VIF) eine nach der anderen entfernt werden, bis die VIF-Werte für die restlichen erklärenden Variablen unter 7,5 liegen.
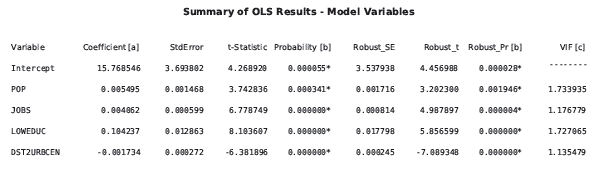
Im nächsten Abschnitt der Ausgabeberichtsdatei werden die Ergebnisse der OLS-Diagnoseprüfungen aufgeführt. Diese Seite enthält auch Hinweise zur Interpretation mit einer Erläuterung zur Wichtigkeit der einzelnen Prüfungen. Wenn Ihr Modell bei einer dieser Diagnoseprüfungen Fehler aufweist, finden Sie in der Tabelle mit allgemeinen Regressionsproblemen Informationen zum Schweregrad der einzelnen Probleme und mögliche Korrekturmaßnahmen. Mithilfe der Diagramme auf den restlichen Seiten des Berichts können Sie Probleme mit Ihrem Modell erkennen und diese beheben.

Der dritte Abschnitt der Ausgabeberichtsdatei umfasst Histogramme, die die Verteilung der einzelnen Variablen im Modell darstellen, sowie Streudiagramme, die die Beziehung der abhängigen Variablen zu den einzelnen erklärenden Variablen anzeigen. Wenn Sie Probleme mit Modellverzerrung haben (worauf ein statistisch signifikanter Jarque-Bera-p-Wert hinweist), prüfen Sie die Histogramme auf verzerrte Verteilungen. Versuchen Sie, diese Variablen zu transformieren, um Verzerrungen zu eliminieren und die Modell-Performance zu verbessern. Die Streudiagramme geben an, welche Variablen für die Vorhersage am besten geeignet sind. Mit diesen Streudiagrammen können Sie auch eine Prüfung auf nicht lineare Beziehungen zwischen den Variablen durchführen. In einigen Fällen können durch das Transformieren einer oder mehrerer Variablen nicht lineare Beziehungen korrigiert und die Modellverzerrung eliminiert werden. Ausreißer in den Daten können auch zu einem verzerrten Modell führen. Überprüfen Sie sowohl die Histogramme als auch die Streudiagramme auf diese Datenwerte und Datenbeziehungen. Führen Sie das Modell mit und ohne Ausreißer aus, um zu ermitteln, inwieweit sich dies auf die Ergebnisse auswirkt. Sie stellen möglicherweise fest, dass es sich bei dem Ausreißer um ungültige Daten handelt (fehlerhaft eingegeben oder aufgezeichnet), und können das zugehörige Feature eventuell aus dem Dataset entfernen. Wenn es sich bei dem Ausreißer um gültige Daten handelt und er signifikante Auswirkungen auf die Ergebnisse der Analyse hat, können Sie einen Ergebnisbericht sowohl mit als auch ohne Ausreißer erstellen.
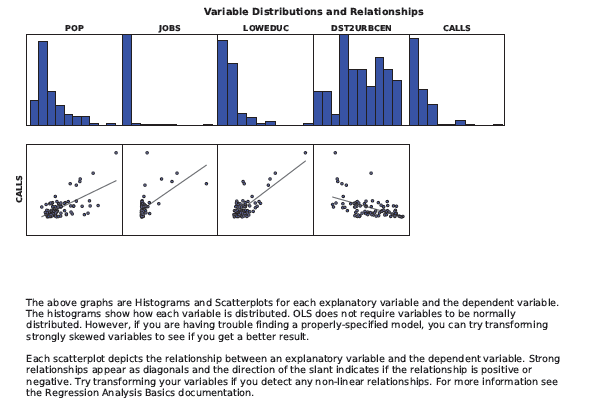
Wenn Sie über ein ordnungsgemäß spezifiziertes Modell verfügen, spiegeln die zu niedrigen und zu hohen Vorhersagen ein Zufallsrauschen wider. Wenn Sie mit dem Zufallsrauschen ein Histogramm erstellen würden, wäre dies normal verteilt (Glockenkurve). Der vierte Abschnitt der Ausgabeberichtsdatei stellt ein Histogramm der zu niedrigen und zu hohen Vorhersagen des Modells dar. Die Balken des Histogramms zeigen die tatsächliche Verteilung, und die über das Histogramm gelegte blaue Linie gibt die Form an, die das Histogramm bei einer normalen Verteilung der Residuen aufweisen würde. Da Perfektion hier nicht wahrscheinlich ist, sollten Sie anhand des Jarque-Bera-Tests ermitteln, ob die Abweichung von einer Normalverteilung statistisch signifikant ist.
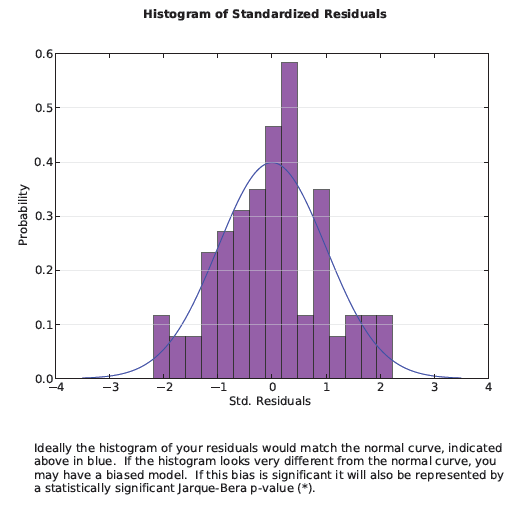
Mit der Koenker-Diagnose können Sie ermitteln, ob die zu modellierenden Beziehungen sich entweder im Untersuchungsgebiet ändern (Nichtstationarität) oder in Bezug auf den Betrag der Variablen, die Sie versuchen vorherzusagen, variieren (Heteroskedastizität). Geographisch gewichtete Regression löst Probleme mit Nichtstationarität. Das Diagramm in Abschnitt 5 der Ausgabeberichtsdatei zeigt an, ob ein Problem mit der Heteroskedastizität vorliegt. Das (unten aufgeführte) Streudiagramm stellt die Beziehungen zwischen den Modellresiduen und den vorhergesagten Werten dar. Angenommen, Sie möchten Kriminalitätsraten modellieren. Wenn das Diagramm eine Kegelform aufweist, wobei sich die Spitze links und die weiteste Ausdehnung rechts im Diagramm befindet, weist dies darauf hin, dass das Modell in Gebieten mit einer niedrigen Kriminalitätsrate eine gute Vorhersage leistet, nicht jedoch in Gebieten mit einer hohen Kriminalitätsrate.
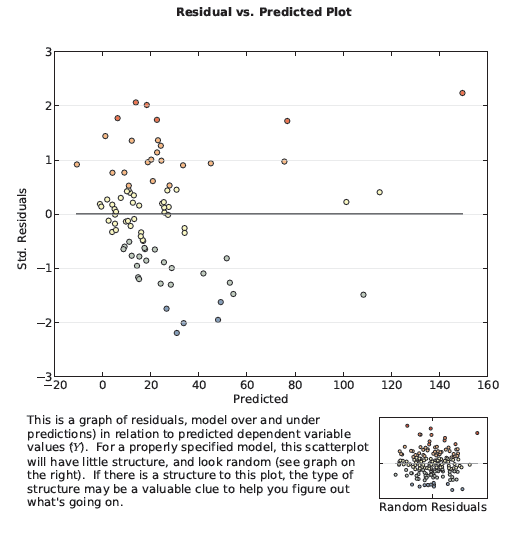
Auf der letzten Seite des Berichts sind die Parametereinstellungen aufgeführt, die zur Ausführungszeit des Berichts verwendet wurden.
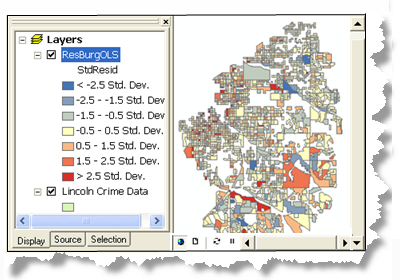
Untersuchen Sie die Modellresiduen in der Ausgabe-Feature-Class. Zu hohe und zu niedrige Vorhersagen für ein korrekt angegebenes Regressionsmodell werden zufällig verteilt. Die Cluster-Bildung für zu hohe und zu niedrige Vorhersagen deutet darauf hin, dass mindestens eine wichtige erklärende Variable fehlt. Überprüfen Sie die Muster in den Modellresiduen, um zu sehen, ob sie Anhaltspunkte zu den fehlenden Variablen liefern. Die Ausführung einer Hot-Spot-Analyse für Regressionsresiduen kann manchmal zum Ermitteln umfangreicherer Muster hilfreich sein. Weitere Strategien zum Umgang mit nicht ordnungsgemäß spezifizierten Modellen finden Sie unter Was Sie noch nicht über die Regressionsanalyse wussten.
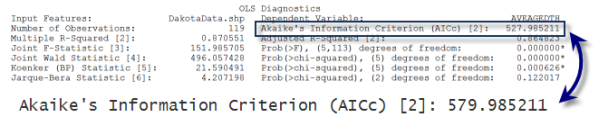
Zeigen Sie die Koeffizienten- und Diagnosetabellen an. Das Erstellen der Koeffizienten- und Diagnosetabellen ist optional. Im Rahmen des Prozesses zur Suche eines effektiven Modells können Sie die Entscheidung treffen, diese Tabellen nicht zu erstellen. Der Modellerstellungsprozess ist iterativ, und wahrscheinlich werden Sie verschiedene Modelle (unterschiedliche erklärende Variablen) ausprobieren, bis Sie sich für einige gute Modelle entscheiden. Sie können das korrigierte Akaike Information Criterion (AICc) in dem Bericht verwenden, um unterschiedliche Modelle zu vergleichen. Das Modell mit dem kleineren AICc-Wert ist das bessere Modell (d. h. unter Berücksichtigung der Modellkomplexität bietet das Modell mit dem kleineren AICc-Wert eine bessere Übereinstimmung mit den beobachteten Daten).
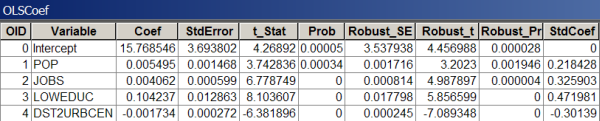
Beim Erstellen der Koeffizienten- und Diagnosetabellen für Ihre finalen OLS-Modelle werden wichtige Elemente des OLS-Berichts erfasst. Die Koeffiziententabelle enthält die Liste der erklärenden Variablen, die in dem Modell verwendet werden, mit ihren Koeffizienten, standardisierten Koeffizienten, Standardfehlern und Wahrscheinlichkeiten. Der Koeffizient spiegelt die erwartete Änderung in der abhängigen Variable pro Einheitenänderung in der zugeordneten erklärenden Variable wider. Die Einheiten für die Koeffizienten stimmen mit den erklärenden Variablen überein. Wenn Sie beispielsweise über eine erklärende Variable für Gesamtbevölkerung verfügen, spiegeln die Koeffizienteneinheiten für diese Variable Personen wider, handelt es sich um eine andere erklärende Variable für Entfernung (Meter) vom Bahnhof, spiegeln die Koeffizienteneinheiten Meter wider. Wenn die Koeffizienten in Standardabweichungen konvertiert werden, werden Sie als Standardkoeffizienten bezeichnet. Sie können die Auswirkungen unterschiedlicher erklärender Variablen auf die abhängige Variable anhand von standardisierten Koeffizienten vergleichen. Die erklärende Variable mit dem größten standardisierten Koeffizienten nach dem Entfernen des "+/-"-Zeichens (absoluter Wert) hat die größten Auswirkungen auf die abhängige Variable. Interpretationen von Koeffizenten können jedoch nur im Vergleich zum Standardfehler ausgeführt werden. Standardfehler geben an, wie wahrscheinlich Sie die gleichen Koeffizienten erhalten, wenn Sie Stichproben für die Daten durchführen und Ihr Modell beliebig oft neu kalibrieren. Eine große Anzahl von Standardfehlern für einen Koeffizienten bedeutet, dass das Resampling in einer Vielzahl möglicher Koeffizientenwerte resultieren würde, eine kleine Anzahl von Standardfehlern gibt an, dass der Koeffizient ziemlich konstant bleibt.
Die Diagnosetabelle enthält die Ergebnisse jedes Diagnosetests und Richtlinien für die Interpretation dieser Ergebnisse.

Zusätzliche Ressourcen
Zahlreiche Ressourcen, mit denen Sie mehr über die OLS-Regression erfahren können, finden Sie auf der Seite Spatial Statistics Resources. Beginnen Sie mit Grundlagen zur Regressionsanalyse, oder arbeiten Sie das Lernprogramm zur Regressionsanalyse durch. Wenden Sie die Regressionsanalyse auf Ihre eigenen Daten an, wobei Sie die Tabelle mit häufigen Problemen und das Thema Was Sie noch nicht über die Regressionsanalyse wussten zurate ziehen, um mehr über zusätzliche Strategien zu erfahren. Wenn Sie kein ordnungsgemäß spezifiziertes Modell finden können, kann das Werkzeug Regressionsanalyse hilfreich sein.
Folgende Ressourcen sind ebenfalls hilfreich:
- Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. Esri Press, 2005.
- Wooldridge, J. M. Introductory Econometrics: A Modern Approach. South-Western, Mason, Ohio, 2003.
- Hamilton, Lawrence C. Regression with Graphics. Brooks/Cole, 1992.