| Beschriftung | Erläuterung | Datentyp |
Eingabe-Features | Die Feature-Class mit Feldern, die für die Werte Abhängige Variable und Erklärende Variable stehen. | Feature Layer |
Abhängige Variable | Das numerische Feld, das für die Werte der abhängigen Variable steht. Bei der Kategorisierung der Beziehungen dient der Wert Erklärende Variable zur Vorhersage des Wertes Abhängige Variable. | Field |
Erklärende Variable | Das numerische Feld, das für die Werte der erklärenden Variable steht. Bei der Kategorisierung der Beziehungen dient der Wert Erklärende Variable zur Vorhersage des Wertes Abhängige Variable. | Field |
Ausgabe-Features | Die Ausgabe-Feature-Class, die alle Eingabe-Features mit Feldern enthält, die für den Wert Abhängige Variable, den Wert Erklärende Variable, den Entropiewert, den Pseudo-p-Wert, das Signifikanzniveau, die Art der kategorisierten Beziehung und Diagnosen im Zusammenhang mit der Kategorisierung stehen. | Feature Class |
Anzahl der Nachbarn (optional) | Die Anzahl der Nachbarn um jedes Feature (einschließlich des Features selbst), die zum Testen einer lokalen Beziehung zwischen den Variablen verwendet werden. Die Anzahl der Nachbar muss zwischen 30 und 1000 liegen; der Standardwert ist 30. Der angegebene Wert sollte groß genug sein, um die Beziehung zwischen Features erkennen zu können, aber noch klein genug, um auch lokale Muster ausmachen zu können. | Long |
Anzahl der Permutationen (optional) | Gibt die Anzahl der Permutationen an, die zur Berechnung des Pseudo-p-Wertes für die einzelnen Feature verwendet werden. Bei der Auswahl der Anzahl von Permutationen muss zwischen Genauigkeit im Pseudo-p-Wert und erhöhter Verarbeitungszeit abgewogen werden.
| Long |
Pop-ups für lokale Scatterplots aktivieren (optional) | Gibt an, ob für die einzelnen Ausgabe-Features Scatterplot-Pop-ups generiert werden. Jeder Scatterplot zeigt die Werte der erklärenden Variable (horizontale Achse) und der abhängigen Variable (vertikale Achse) in der lokalen Nachbarschaft zusammen mit einer passenden Linie oder Kurve zur Visualisierung der Beziehungsform an. Scatterplot-Diagramme werden für Shapefile-Ausgaben nicht unterstützt.
| Boolean |
Konfidenzniveau (optional) | Gibt ein Konfidenzniveau des Hypothesentestes für signifikante Beziehungen an.
| String |
FDR-Korrektur anwenden (False Discovery Rate) (optional) | Gibt an, ob eine FDR-Korrektur (False Discovery Rate) auf die Pseudo-p-Werte angewendet wird.
| Boolean |
Skalierungsfaktor (Alpha) (optional) | Der Grad der Empfindlichkeit für schwächere Beziehungen zwischen den Variablen. Mit größeren Werten (näher an 1) können relativ schwache Beziehungen erkannt werden, während niedrigere Werte (näher an 0) nur starke Beziehungen erkennen. Niedrigere Werte sind auch weniger anfällig für Ausreißer. Der Wert muss zwischen 0,01 und 1 liegen; der Standardwert ist 0,5. | Double |
Zusammenfassung
Analysiert zwei Variablen für statistisch signifikante Beziehungen mithilfe lokaler Entropie. Jedes Feature wird basierend auf dem Beziehungstyp in eine von sechs Kategorien klassifiziert. Die Ausgabe kann dazu verwendet werden, Bereiche zu visualisieren, deren Variablen miteinander in Beziehung stehen, und Veränderungen in ihren Beziehungen über das gesamte Untersuchungsgebiet zu erkunden.
Weitere Informationen zur Funktionsweise von "Lokale bivariate Beziehungen"
Abbildung
Verwendung
Dieses Werkzeug akzeptiert Punkte und Polygone als Eingabe und sollte mit kontinuierlichen Variablen verwendet werden. Es ist nicht geeignet für binäre oder kategorisierte Daten.
Es empfiehlt sich, die Ausgabe-Features nicht als Shapefile (.shp), sondern in einer Geodatabase zu speichern. In Shapefiles können keine NULL-Werte in Attributen und keine Diagramme in Pop-up-Dialogfeldern gespeichert werden.
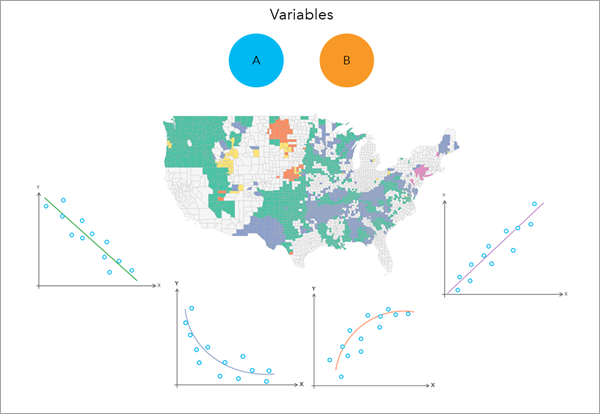
Je nachdem, wie zuverlässig der Parameter Erklärende Variable den Parameterwert Abhängige Variable vorhersagen kann, wird jedes Eingabe-Feature einer der folgenden Beziehungskategorien zugeordnet:
- Nicht signifikant: Die Beziehung zwischen den Variablen ist nicht statistisch signifikant.
- Positiv linear: Die abhängige Variable steigt in dem Maße linear an, wie die erklärende Variable ansteigt.
- Negativ linear: Die abhängige Variable sinkt in dem Maße linear, wie die erklärende Variable sinkt.
- Konkav: Die abhängige Variable ändert sich in dem Maße in eine konkave Kurve, wie die erklärende Variable zunimmt.
- Konvex: Die abhängige Variable ändert sich in dem Maße in eine konvexe Kurve, wie die erklärende Variable zunimmt.
- Undefiniert komplex: Die Variablen stehen in einer signifikanten Beziehung, aber die Art der Beziehung kann durch keine andere Kategorie zuverlässig beschrieben werden.
Ob eine Beziehung zwischen zwei Variablen besteht, ist nicht davon abhängig, welche von ihnen als erklärende Variable und welche als abhängige Variable deklariert ist. Wenn beispielsweise Diabetes in Beziehung steht zu Adipositas, steht Adipositas ebenfalls in einer Beziehung zu Diabetes. Die Klassifizierung der Beziehung zwischen zwei Variablen kann sich jedoch ändern, je nachdem, welche von ihnen als erklärende Variable und welche als abhängige Variable deklariert ist. Möglicherweise sagt eine Variable eine zweite Variable präzise vorher, während die zweite Variable die erste nicht präzise vorhersagt. Wenn Sie unsicher sind, welche Variable erklärend und welche abhängig sein soll, führen Sie das Werkzeug zweimal aus, und versuchen Sie beides.
Dieses Werkzeug unterstützt eine Parallelverarbeitung und nutzt standardmäßig 50 Prozent der verfügbaren Prozessoren. Die Anzahl der Prozessoren kann mit der Umgebung Faktor für parallele Verarbeitung erhöht oder verringert werden.
Parameter
arcpy.stats.LocalBivariateRelationships(in_features, dependent_variable, explanatory_variable, output_features, {number_of_neighbors}, {number_of_permutations}, {enable_local_scatterplot_popups}, {level_of_confidence}, {apply_false_discovery_rate_fdr_correction}, {scaling_factor})| Name | Erläuterung | Datentyp |
in_features | Die Feature-Class mit Feldern, die für die Werte dependent_variable und explanatory_variable stehen. | Feature Layer |
dependent_variable | Das numerische Feld, das für die Werte der abhängigen Variable steht. Bei der Kategorisierung der Beziehungen dient der Wert explanatory_variable zur Vorhersage des Wertes dependent_variable. | Field |
explanatory_variable | Das numerische Feld, das für die Werte der erklärenden Variable steht. Bei der Kategorisierung der Beziehungen dient der Wert explanatory_variable zur Vorhersage des Wertes dependent_variable. | Field |
output_features | Die Ausgabe-Feature-Class, die alle Eingabe-Features mit Feldern enthält, die für den Wert dependent_variable, den Wert explanatory_variable, den Entropiewert, den Pseudo-p-Wert, das Signifikanzniveau, die Art der kategorisierten Beziehung und Diagnosen im Zusammenhang mit der Kategorisierung stehen. | Feature Class |
number_of_neighbors (optional) | Die Anzahl der Nachbarn um jedes Feature (einschließlich des Features selbst), die zum Testen einer lokalen Beziehung zwischen den Variablen verwendet werden. Die Anzahl der Nachbar muss zwischen 30 und 1000 liegen; der Standardwert ist 30. Der angegebene Wert sollte groß genug sein, um die Beziehung zwischen Features erkennen zu können, aber noch klein genug, um auch lokale Muster ausmachen zu können. | Long |
number_of_permutations (optional) | Gibt die Anzahl der Permutationen an, die zur Berechnung des Pseudo-p-Wertes für die einzelnen Feature verwendet werden. Bei der Auswahl der Anzahl von Permutationen muss zwischen Genauigkeit im Pseudo-p-Wert und erhöhter Verarbeitungszeit abgewogen werden.
| Long |
enable_local_scatterplot_popups (optional) | Gibt an, ob für die einzelnen Ausgabe-Features Scatterplot-Pop-ups generiert werden. Jeder Scatterplot zeigt die Werte der erklärenden Variable (horizontale Achse) und der abhängigen Variable (vertikale Achse) in der lokalen Nachbarschaft zusammen mit einer passenden Linie oder Kurve zur Visualisierung der Beziehungsform an. Scatterplot-Diagramme werden für Shapefile-Ausgaben nicht unterstützt.
| Boolean |
level_of_confidence (optional) | Gibt ein Konfidenzniveau des Hypothesentestes für signifikante Beziehungen an.
| String |
apply_false_discovery_rate_fdr_correction (optional) | Gibt an, ob eine FDR-Korrektur (False Discovery Rate) auf die Pseudo-p-Werte angewendet wird.
| Boolean |
scaling_factor (optional) | Der Grad der Empfindlichkeit für schwächere Beziehungen zwischen den Variablen. Mit größeren Werten (näher an 1) können relativ schwache Beziehungen erkannt werden, während niedrigere Werte (näher an 0) nur starke Beziehungen erkennen. Niedrigere Werte sind auch weniger anfällig für Ausreißer. Der Wert muss zwischen 0,01 und 1 liegen; der Standardwert ist 0,5. | Double |
Codebeispiel
Das folgende Skript für das Python-Fenster veranschaulicht, wie Sie die Funktion LocalBivariateRelationships verwenden.
import arcpy
arcpy.env.workspace = 'C:\\LBR\\MyData.gdb'
arcpy.stats.LocalBivariateRelationships('ObesityDiabetes', 'ObesityRate',
'DiabetesRate','LBR_Results', 30, '199', 'CREATE_POPUP',
'95%', 'APPLY_FDR', 0.5)Im folgenden eigenständigen Python-Skript wird veranschaulicht, wie Sie die Funktion LocalBivariateRelationships verwenden.
# Use the Local Bivariate Relationships tool to study the relationship between
# obesity and diabetes.
# Import system modules.
import arcpy
import os
# Set property to overwrite existing output by default.
arcpy.env.overwriteOutput = True
try:
# Set the workspace and input features.
arcpy.env.workspace = r"C:\\LBR\\MyData.gdb"
inputFeatures = 'ObesityDiabetes'
# Set the output workspace and output name.
outws = 'C:\\LBR\\outputs.gdb'
outputName = 'LBR_Results'
# Set input features, dependent variable, and explanatory variable.
depVar = 'DiabetesRate'
explVar = 'ObesityRate'
# Set number of neighbors and permutations.
numNeighbors = 50
numPerms = '999'
# Choose to create pop-ups.
popUps = 'CREATE_POPUP'
# Choose confidence level and apply False Discovery Rate correction.
confLevel = '95%'
fdr = 'APPLY_FDR'
# Set the scaling factor.
scaleFactor = 0.5
# Run Local Bivariate Relationships.
arcpy.stats.LocalBivariateRelationships(inputFeatures, depVar, explVar,
os.path.join(outws, outputName),
numNeighbors, numPerms, popUps,
confLevel, fdr, scaleFactor)
except arcpy.ExecuteError:
# If an error occurred when running the tool, print the error message.
print(arcpy.GetMessages())Lizenzinformationen
- Basic: Ja
- Standard: Ja
- Advanced: Ja