| Beschriftung | Erläuterung | Datentyp |
Eingabe-Feature-Class | Die Feature-Class, die das abhängige Element und die unabhängigen Variablen für die Analyse enthält. | Feature Layer |
Eindeutiges ID-Feld | Ein ganzzahliges Feld, das für jedes Feature in der Eingabe-Feature-Class einen anderen Wert enthält. | Field |
Ausgabe-Feature-Class | Die Ausgabe-Feature-Class, die abhängige Variablenschätzungen und Residuen empfängt. | Feature Class |
Abhängige Variable | Das Zahlenfeld, das Werte für den geplanten Modellierungsvorgang enthält. | Field |
Erklärende Variablen | Eine Liste von Feldern, die erklärende Variablen im Regressionsmodell darstellt. | Field |
Koeffizienten-Ausgabetabelle (optional) | Der vollständige Pfad zu einer optionalen Tabelle, in der Modellkoeffizienten, standardisierte Koeffizienten und Wahrscheinlichkeiten für jede erklärende Variable empfangen werden. | Table |
Diagnose-Ausgabetabelle (optional) | Der vollständige Pfad zu einer optionalen Tabelle, in der Modellzusammenfassungsdiagnosen empfangen werden. | Table |
Ausgabeberichtsdatei (optional) | Der Pfad zur optionalen PDF-Datei, die vom Werkzeug erstellt wird. Diese Berichtsdatei enthält eine Modelldiagnose, Diagramme und Hinweise zur Interpretation der OLS-Ergebnisse. | File |
Zusammenfassung
Führt eine globale lineare OLS-Regression aus, um Vorhersagen zu generieren oder eine abhängige Variable in Hinsicht auf ihre Beziehungen zu einem Satz erklärender Variablen zu modellieren.
Hinweis:
Die Funktionalität dieses Werkzeugs ist im Werkzeug Generalisierte lineare Regression enthalten, das in ArcGIS Pro 2.3 hinzugefügt wurde. Das Werkzeug Generalisierte lineare Regression enthält zusätzliche Modelle.
Abbildung
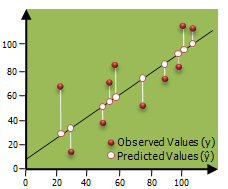
Verwendung
-
Primäre Ausgabe dieses Werkzeugs ist eine Berichtsdatei, die während der Ausführung des Werkzeugs in Form von Meldungen unten im Bereich Geoverarbeitung ausgegeben wird. Sie können auf diese Meldungen zugreifen, indem Sie mit der Maus auf die Fortschrittsleiste zeigen, auf die Pop-out-Schaltfläche klicken oder den Abschnitt "Meldungen" im Bereich Geoverarbeitung erweitern. Sie können auch über den Geoverarbeitungsverlauf auf die Meldungen für eine zuvor ausgeführte Regressionsanalyse zugreifen.
-
Das OLS-Werkzeug erzeugt auch eine Ausgabe-Feature-Class und optionale Tabellen mit Koeffizienteninformationen und Diagnosen. Diese können im unteren Bereich des Fensters Geoverarbeitung unter "Meldungen" aufgerufen werden. Die Ausgabe-Feature-Class wird automatisch dem Inhaltsverzeichnis hinzugefügt, wobei ein Hot/Cold-Rendering-Schema zur Modellierung von Residuen angewendet wird. Eine vollständige Erläuterung der einzelnen Ausgaben finden Sie im Thema Funktionsweise der OLS-Regression.
-
Die Ergebnisse der OLS-Regression sind jedoch nur dann zuverlässig, wenn die Daten und das Regressionsmodell allen Annahmen entsprechen, die für diese Methode erforderlich sind. Schlagen Sie in der Tabelle Allgemeine Regressionsprobleme, Folgen und Lösungen unter Grundlagen zur Regressionsanalyse nach, um sicherzustellen, dass das Modell ordnungsgemäß angegeben ist.
-
Abhängige und erklärende Variablen sollten Zahlenfelder sein, die eine Vielzahl von Werten enthalten. Die OLS-Regression kann keine Berechnung vornehmen, wenn die Variablen alle denselben Wert aufweisen (wenn beispielsweise alle Werte für ein Feld 9,0 betragen). Lineare Regressionsmethoden wie OLS sind nicht für das Vorhersagen von binären Ergebnissen geeignet (wenn z. B. alle Werte für die abhängige Variable entweder 1 oder 0 betragen).
-
Über das Feld Unique ID werden die Modellvorhersagen mit den einzelnen Features verknüpft. Infolgedessen müssen die Werte unter Unique ID für jedes Feature eindeutig sein und in einem permanenten Feld angegeben werden, das in der Feature-Class beibehalten wird. Falls das Feld Unique ID nicht vorhanden ist, können Sie dieses erstellen, indem Sie der Feature-Class-Tabelle ein neues ganzzahliges Feld hinzufügen. Berechnen Sie die Feldwerte so, dass sie dem Feld FID/OID entsprechen. Sie können das Feld FID/OID nicht direkt für den Parameter Eindeutige ID verwenden.
-
Immer wenn eine statistisch signifikante räumliche Autokorrelation der Regressionsresiduen auftritt, wird das OLS-Modell als falsch angegeben angesehen. Die Ergebnisse der OLS-Regression sind infolgedessen unzuverlässig. Stellen Sie sicher, dass Sie das Werkzeug Räumliche Autokorrelation für die Regressionsresiduen ausführen, um dieses potenzielle Problem zu beheben. Die statistisch signifikante räumliche Autokorrelation in den Regressionsresiduen weist fast immer darauf hin, dass eine oder mehrere wichtige erklärende Variablen im Modell fehlen.
-
Sichten Sie die in Ihren Regressionsresiduen vorhandenen zu hohen und zu niedrigen Vorhersagen, um festzustellen, ob sie Aufschluss über potenzielle fehlende Variablen in Ihrem Regressionsmodell geben. Es kann hilfreich sein, eine Hot-Spot-Analyse für die Residuen durchzuführen, um so die räumliche Cluster-Bildung der zu hohen und zu niedrigen Vorhersagen besser visualisieren zu können.
-
Wenn die Modellierung von nicht stationären Variablen mithilfe eines globalen Modells (wie OLS) zu falschen Angaben führt, kann Geographisch gewichtete Regression verwendet werden, um die Vorhersagen zu verbessern und die Nichtstationarität (regionale Variation) der erklärenden Variablen besser zu verstehen.
-
Wenn das Ergebnis einer Berechnung unendlich oder nicht definiert ist, lautet die Ausgabe für Nicht-Shapefiles NULL; für Shapefiles lautet die Ausgabe –DBL_MAX (beispielsweise –1,7976931348623158e+308).
-
Modellzusammenfassungsdiagnosen werden in den OLS-Zusammenfassungsbericht und in die optionale Diagnose-Ausgabetabelle geschrieben. Beide enthalten Diagnosen für das korrigierte Akaike Information Criterion (AICc), das Bestimmtheitsmaß, die Joint F Statistic, die Wald Statistic, die Koenker Breusch-Pagan Statistic und die Jarque-Bera Statistic. Die Diagnosetabelle enthält zudem nicht korrigierte AIC- und Sigma-Squared-Werte.
-
Der optionale Koeffizient und, sofern bereits vorhanden, die Diagnose-Ausgabetabellen werden überschrieben, wenn die Option Geoverarbeitungswerkzeugen das Überschreiben vorhandener Datasets erlauben aktiviert ist.
-
Auf Computern, die mit ArcGIS-Sprachpaketen für Arabisch und andere von rechts nach links verlaufende Sprachen konfiguriert sind, kann Text fehlen oder es können Formatierungsprobleme in der PDF-Ausgabeberichtsdatei auftreten. Weitere Informationen zum Beheben dieser Probleme finden Sie in diesem Artikel.
-
Sie können Karten-Layer verwenden, um die Eingabe-Feature-Class zu definieren. Beim Verwenden eines Layers mit einer Auswahl sind nur die ausgewählten Features in der Analyse enthalten.
Vorsicht:
Denken Sie beim Verwenden von Shapefiles daran, dass diese keine NULL-Werte speichern können. Werkzeuge oder andere Verfahren zur Erstellung von Shapefiles aus Nicht-Shapefile-Eingaben speichern oder interpretieren NULL-Werte möglicherweise als Wert 0. In manchen Fällen werden NULL-Werte in Shapefiles als sehr große negative Werte gespeichert. Dies kann zu unerwarteten Ergebnissen führen. Weitere Informationen finden Sie unter Überlegungen zur Geoverarbeitung für die Shapefile-Ausgabe.
Parameter
arcpy.stats.OrdinaryLeastSquares(Input_Feature_Class, Unique_ID_Field, Output_Feature_Class, Dependent_Variable, Explanatory_Variables, {Coefficient_Output_Table}, {Diagnostic_Output_Table}, {Output_Report_File})| Name | Erläuterung | Datentyp |
Input_Feature_Class | Die Feature-Class, die das abhängige Element und die unabhängigen Variablen für die Analyse enthält. | Feature Layer |
Unique_ID_Field | Ein ganzzahliges Feld, das für jedes Feature in der Eingabe-Feature-Class einen anderen Wert enthält. | Field |
Output_Feature_Class | Die Ausgabe-Feature-Class, die abhängige Variablenschätzungen und Residuen empfängt. | Feature Class |
Dependent_Variable | Das Zahlenfeld, das Werte für den geplanten Modellierungsvorgang enthält. | Field |
Explanatory_Variables [Explanatory_Variables,...] | Eine Liste von Feldern, die erklärende Variablen im Regressionsmodell darstellt. | Field |
Coefficient_Output_Table (optional) | Der vollständige Pfad zu einer optionalen Tabelle, in der Modellkoeffizienten, standardisierte Koeffizienten und Wahrscheinlichkeiten für jede erklärende Variable empfangen werden. | Table |
Diagnostic_Output_Table (optional) | Der vollständige Pfad zu einer optionalen Tabelle, in der Modellzusammenfassungsdiagnosen empfangen werden. | Table |
Output_Report_File (optional) | Der Pfad zur optionalen PDF-Datei, die vom Werkzeug erstellt wird. Diese Berichtsdatei enthält eine Modelldiagnose, Diagramme und Hinweise zur Interpretation der OLS-Ergebnisse. | File |
Codebeispiel
Das folgende Skript für das Python-Fenster veranschaulicht, wie Sie die Funktion OrdinaryLeastSquares verwenden.
import arcpy
arcpy.env.workspace = r"c:\data"
arcpy.stats.OrdinaryLeastSquares("USCounties.shp", "MYID", "olsResults.shp",
"GROWTH","LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
"olsCoefTab.dbf", "olsDiagTab.dbf")Im folgenden eigenständigen Python-Skript wird veranschaulicht, wie Sie die Funktion OrdinaryLeastSquares verwenden.
# Analyze the growth of regional per capita incomes in US
# Counties from 1969 -- 2002 using Ordinary Least Squares Regression
# Import system modules
import arcpy
# Set property to overwrite existing outputs
arcpy.env.overwriteOutput = True
# Local variables...
workspace = r"C:\Data"
try:
# Set the current workspace (to avoid having to specify the full path to the feature classes each time)
arcpy.env.workspace = workspace
# Growth as a function of {log of starting income, dummy for South
# counties, interaction term for South counties, population density}
# Process: Ordinary Least Squares...
ols = arcpy.stats.OrdinaryLeastSquares("USCounties.shp", "MYID",
"olsResults.shp", "GROWTH",
"LOGPCR69;SOUTH;LPCR_SOUTH;PopDen69",
"olsCoefTab.dbf",
"olsDiagTab.dbf")
# Create Spatial Weights Matrix (Can be based on input or output FC)
# Process: Generate Spatial Weights Matrix...
swm = arcpy.stats.GenerateSpatialWeightsMatrix("USCounties.shp", "MYID",
"euclidean6Neighs.swm",
"K_NEAREST_NEIGHBORS",
"#", "#", "#", 6)
# Calculate Moran's Index of Spatial Autocorrelation for
# OLS Residuals using a SWM File.
# Process: Spatial Autocorrelation (Morans I)...
moransI = arcpy.stats.SpatialAutocorrelation("olsResults.shp", "Residual",
"NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "NONE", "#",
"euclidean6Neighs.swm")
except:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())Umgebungen
Lizenzinformationen
- Basic: Ja
- Standard: Ja
- Advanced: Ja
Verwandte Themen
- Überblick über das Toolset "Modellierung von räumlichen Beziehungen"
- Suchen eines Geoverarbeitungswerkzeugs
- Funktionsweise von "Geographisch gewichtete Regression"
- Grundlagen zur Regressionsanalyse
- Geographisch gewichtete Regression (GWR)
- Räumliche Autokorrelation (Morans I)
- Hot-Spot-Analyse (Getis-Ord Gi*)
- Was ist ein Z-Wert? Was ist ein p-Wert?
- Funktionsweise der OLS-Regression
- Was Sie noch nicht über die Regressionsanalyse wussten
- Regressionsanalyse
- Interpretieren der Ergebnisse des Werkzeugs "Regressionsanalyse"
- Funktionsweise der Regressionsanalyse