How Assign Weights by Pairwise Comparison works

The Assign Weights by Pairwise Comparison tool calculates weights from a series of input variables by allowing you to evaluate the variables in pairs. On the tool dialog box, the pairs are automatically created from the input variables. Each pair has an accompanying slider that can be adjusted to indicate which variable is more important and by how much. A comparison matrix is created from the pairwise evaluations from which the weights are calculated.

The weights can be used in a suitability model in Spatial Analyst that uses the Weighted Sum tool, in the Suitability Modeler, or in a suitability model built in Business Analyst. The weights can also be used as the variable weights in the Calculate Composite Index tool in spatial statistics.

Pairwise comparison

In a suitability model, determining the weights for many variables (or criteria) to identify their relative importance is difficult and subjective. However, you can more accurately compare pairs of variables. For example, you may be challenged if asked to identify the weights for five criteria (slope, aspect, distance to water, distance to roads, and elevation) relative to one another in a suitability model. However, you can more easily identify which criteria, slope or aspect, is more important and by how much.

The pairwise comparison method (Saaty 2008) is widely used in various fields where the multicriteria decision-making approach is used, such as ecological habitat modeling, business site selection, and identifying health risk indices. The advantage of pairwise weighting is by comparing items two at a time, it simplifies complex decisions and provides a systematic way to prioritize or rank the input variables. Since you can more accurately compare pairs of variables relative to one another, the final calculated weights are more objective. To ensure that the pairwise comparisons are consistent (for example, if A > B, and B > C, C cannot be greater than A), the tool provides diagnostics functionality.

Example applications

Example applications of pairwise comparison include the following:

• Calculate the weights for multiple criteria in a suitability model.
• Determine the weights for a set of submodels for a composite suitability model.
• Assess the relative importance of different land use types within a layer.
• Compute the relative weights of different pollutants to create an air quality index to influence public policy.
• Identify new class values when reclassifying a raster layer based on preference.
• Estimate the relative priorities for multiple projects in business decision making.

Pairwise methodology

Developed by Thomas L. Saaty (Saaty 2008), pairwise comparison provides a framework to derive relative weights of importance for multiple variables. Instead of simultaneously ranking all the variables, pairwise comparisons provide a structured method to assess the importance of the variables by comparing them two at a time. This approach is particularly useful when dealing with intangible factors that cannot be measured directly but are essential to decision making. This method relies on expert judgments to derive priority scales that measure the factors in relative terms.

Pairwise comparison workflow

The following are the main steps in the pairwise comparison workflow:

1. Identify the variables to compare.
2. Specify the comparisons for the variable pairs and create a comparison matrix.
3. Calculate the weights from the comparison matrix and produce an output table.

The Assign Weights by Pairwise Comparison tool dynamically creates pairs from the input variables. Use the sliders to identify which variable is more important and by how much for each pairing. As each comparison is made, the comparison matrix is updated. The final weights are determined from the comparison matrix.

The tool output is a set of derived weights for the input variables with or without the comparison matrix.

Use the tool to assign weights by pairwise comparison

The following is a common workflow for using the tool. The step numbers below correspond to the numbers in the image above.

1. Provide the names of variables to compare in the Input Variables To Compare parameter.
2. Optionally, alter the automatically generated Output Table parameter value.
3. For the Pairwise Comparison Matrix parameter, click the Compare variables and calculate weights button.

   The Define Pairwise Comparisions window appears containing the Comparison Matrix table.

4. Specify the pairwise comparisons by moving the sliders for each pair.
5. Click Consistency to ensure that the pairwise comparisons are consistent.
6. Click Run.

The tool uses a 1 to 9 scale developed by Saaty (2008). The scale, their definitions, and explanations of each value in the scale are identified in the table below.

Intensity of Importance	Definition	Explanation
1	Equal importance	Two activities contribute equally to the objective.
2	Weak or slight
3	Moderate importance	Experience and judgement slightly favor one activity over the another.
4	Moderate plus
5	Strong importance	Experience and judgement strongly favor one activity over another.
6	Strong plus
7	Very strong or demonstrated importance	An activity is favored very strongly over another; its dominance is demonstrated in practice.
8	Very, very strong
9	Extreme importance	The evidence favoring one activity over another is of the highest possible order of affirmation.

Comparison matrix

Central to the pairwise methodology is the comparison matrix. The matrix is populated with the pairwise preferences from which the weights are calculated.

In the matrix, the intersection of each row with each column represents a pair of variables to compare. On the dialog box, for each pair, adjust the slider to indicate your comparison preference. Moving the slider toward one side shows a stronger preference for that variable. Keeping the slider in the center means both variables are equally important. This process involves making subjective judgments based on your knowledge, experience, or preferences.

The comparison matrix is updated as each slider is moved. The tool assigns the selected values of the sliders to the cell at the corresponding row (the more important variable) and column (the less important variable). Its reciprocal value (1/value) is assigned to the opposite position in the matrix.

For example, if you're evaluating Solar_Gain and Elevation variables in a solar farm suitability model, you might consider Solar_Gain twice as important as Elevation. To reflect this evaluation, adjust the slider for the two variables to the Solar_Gain side between 1 and 3 in the scale. In the Comparison matrix, the Solar_Gain row and Elevation column cell value is updated to 2, and the reciprocal value, (1/2, or 0.5), is automatically assigned to the Elevation row and Solar_Gain column cell.

Pairwise comparison calculations

Calculating the weights from a comparison matrix is a multistep process as illustrated in the image below:

This image illustrates the steps for calculating weights from a comparison matrix.

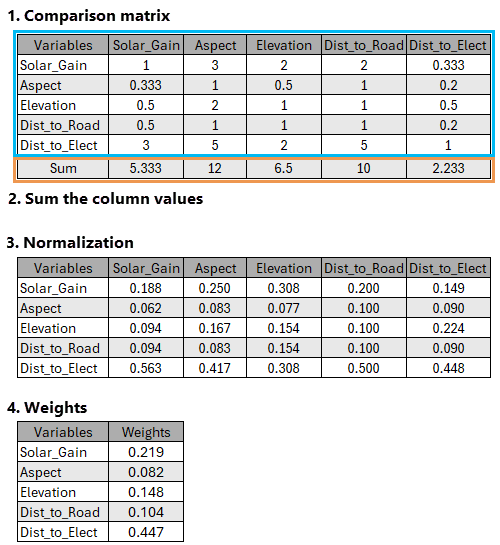
The four steps are described below.

Comparison matrix

Create the comparison matrix identifying the pairwise evaluations for the input variables.

Sum the columns

The tool sums the cell values for each column.

The resulting column total is used to normalize the values within that column. In the pairwise comparison example in the image above, the first column, Solar_Gain, contains the values 1, 0.333, 0.5, 0.5, and 3, which sums to 5.333.

The total of 5.333 will be used to normalize each value in the first column and is used in the next step.

Normalize

Each normalized value for each comparison pair is calculated by dividing the corresponding comparison value by the total of its column.

For example, the normalized value for the Solar_Gain row and Solar_Gain column cell is: 1 / 5.333 ≈ 0.188

Calculate weights

To calculate the final weight for each variable, the average of all the normalized cells in each row is determined.

For the first row in the normalization table matrix in the image above the calculation is as follows:

This calculation is performed for each of the variables to determine their weights.

Adjust the consistency ratio

Click Consistency to review the consistency among the comparisons of all the pairs. The consistency ratio is displayed at the bottom. If the ratio is greater than 0.1, the comparisons are not consistent. The ratio is shown in red as are the three pairs that are most inconsistent (see the example below). You can adjust the inconsistent comparisons using the sliders to ensure consistency.

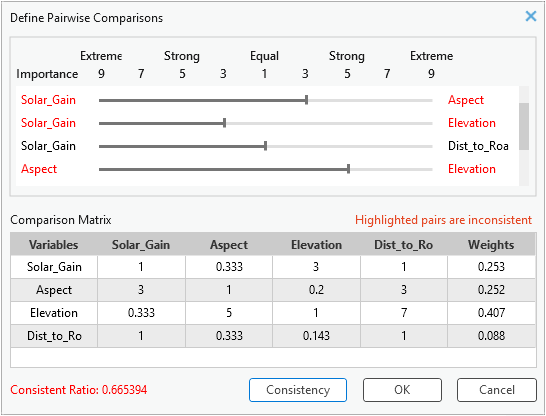
See Calculate the consistency ratio for a detailed discussion on how the consistency ratio is determined.

Input comparison matrix formats

The following are examples of valid formats that can be used as the comparison_matrix parameter value without and with weights.

Without weights

The following is an example of a table format input comparison matrix without weights:

Variables	Dist_Roads	Elevation	Landuse	Aspect
Dist_Roads	1	0.333	3	1
Elevation	3	1	0.2	3
Landuse	0.333	5	1	7
Aspect	1	0.333	0.143	1

There are two text formats for the input comparison matrix without weights.

The first format lists the variables and their evaluations in a text table. The following is an example:

Variables, Dist_Roads, Elevation, Landuse, Aspect
Dist_Roads,1,0.333,3,1
Elevation,3,1,0.2,3
Landuse,0.333,5,1,7
Aspect,1,0.333,0.143,1

The second format lists each of the variable pairs and their evaluations. The following is an example:

Variables
Dist_Roads Elevation 0.333;
Dist_Roads Landuse 3;
Dist_Roads Aspect 1;
Elevation Landuse 0.2;
Elevation Aspect 3;
Landuse Aspect 7;

With weights

The following is an example of a table format input comparison matrix with weights:

Variable	Dist_Roads	Elevation	Landuse	Aspect	Weights
Dist_Roads	1	0.333	3	1	0.253
Elevation	3	1	0.2	3	0.252
Landuse	0.333	5	1	7	0.407
Aspect	1	0.333	0.143	1	0.088

Note:

If the weights have already been calculated, there is little need to use the tool to recalculate them. If the weights are included in the comparison_matrix parameter value, they will be ignored and recalculated by the tool. Including the weights in the matrix is used, in certain cases, when the comparison matrix is from another tool or application.

There are two acceptable formats for text input comparison matrix with weights.

The first format lists the variables and their evaluations and weights in a text table. The following is an example:

Variables, Dist_Roads, Elevation, Landuse, Aspect, Weights
Dist_Roads,1,0.333,3,1,0.253
Elevation,3,1,0.2,3,0.252
Landuse,0.333,5,1,7,0.407
Aspect,1,0.333,0.143,1,0.088

The second format is divided into two section. The first section identifies the variables by listing each of the variable pairs and their evaluations. In the second section, the variables are specified with their final weight. The following is an example:

Variables
Dist_Roads Elevation 0.333;
Dist_Roads Landuse 3;
Dist_Roads Aspect 1;
Elevation Landuse 0.2;
Elevation Aspect 3;
Landuse Aspect 7;
Weights
Dist_Roads 0.252906;
Elevation 0.252138;
Landuse 0.406524;
Aspect 0.088432;

Python comparison matrix

Directly enter the pairs and their evaluations as the comparison_matrix parameter value in Python as follows:

Variables Dist_Roads Elevation 0.333; Dist_Roads Landuse 3; Dist_Roads Aspect 1; Elevation Landuse 0.2; Elevation Aspect 3; Landuse Aspect 7;

Note:

The order of the pairwise comparisons in the table or text file formats or provided as the comparison_matrix parameter value in Python must be in the same order as the input_variables parameter value. In the variable pairing text file format or when provided directly to the parameter, the pairings and their evaluations must list the first variable sequentially paired with each of the other variables. Then, the second variable is sequentially paired with the remaining variables, and so on.

Output table formats

The following are examples of output tables from the tool with and without the comparison matrix.

With the comparison matrix

The following table includes the comparison matrix when the Add comparison matrix to output parameter is checked:

Comparison matrix and accompanying weights

Variable	Dist_Roads	Elevation	Landuse	Aspect	Weights
Dist_Roads	1	0.333	3	1	0.253
Elevation	3	1	0.2	3	0.252
Landuse	0.333	5	1	7	0.407
Aspect	1	0.333	0.143	1	0.088

The following is an example of the output table when the Add comparison matrix to output parameter is checked and the output type is text:

Variables, Dist_Roads, Elevation, Landuse, Aspect, Weights
Dist_Roads,1,0.333,3,1,0.253
Elevation,3,1,0.2,3,0.252
Landuse,0.333,5,1,7,0.407
Aspect,1,0.333,0.143,1,0.088

With weights only

The following formats are used when the Add comparison matrix to output parameter is not checked.

When the output type is specified as a table, the output table contains two columns: Variables and Weights.

Variables	Weights
Dist_Roads	0.253
Elevation	0.252
Landuse	0.407
Aspect	0.088

When the output type is text, the table is a structured text file containing the derived weights for each variable based on the pairwise comparisons. The following is an example:

Variables, Weights
Dist_Roads,0.253
Elevation,0.252
Landuse,0.407
Aspect,0.088

References

Saaty, T. L. 2008. "Decision making with the analytic hierarchy process". International Journal of Services Sciences, 1(1), 83-98.