Ground to grid correction is a drawing mode that converts bearing and distance values to grid measurements defined by the coordinate system of your feature data. It automatically corrects bearing and distance values you enter with ground to grid-aware tools.
COGO ground measurements entered from survey plans and similar land record documents are often different than grid measurements defined by your spatial data. Setting accurate grid correction values ensures that feature geometry is correctly rotated and scaled for a specific plane coordinate system.
In ArcGIS Pro, ground to grid rotates your bearing values by a specified offset angle and scales your distance values by a specified distance factor. The following sections introduce the basic concepts of ground to grid correction as it applies to creating parcel data.
Direction offset
The direction offset is a user-defined angle that converts direction values to grid bearings on the projection surface of your map data. On survey documents, north can be geodetic north, magnetic north, grid north, or a locally defined north.
Surveyors are also free to choose a basis of bearing that is a line between two control points in the field as the baseline for a survey. You can find the basis of bearing or convergence angle as a statement on a survey document noting the two points used for the baseline. For example, Basis of Bearing is S 00'20'00" E 819.85.
Distance factor
The distance factor is a user-defined multiplier that converts ground distances to grid distances as you create geometry. Surveyors measure ground distances between two point locations on a level two-dimensional plane at an elevation above sea level that is effectively the ellipsoidal height.
Although the distance factor is computed at a single point location for a particular deed or subdivision, for most use cases it can be applied to all line distances in the same document, as the distance factor does not vary significantly within an area that is represented in a single document.
While there is a measurable difference between ellipsoidal heights and the height above sea level, this difference is mathematically insignificant when computing a distance factor for most land record data.
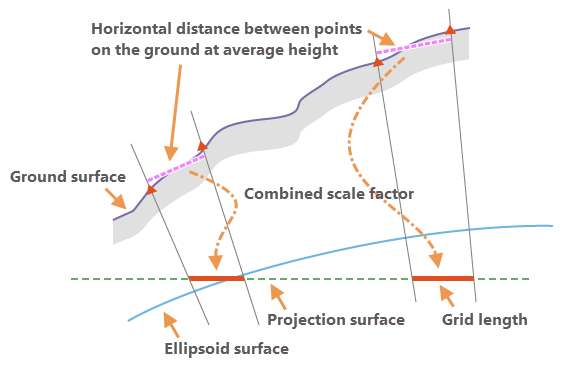
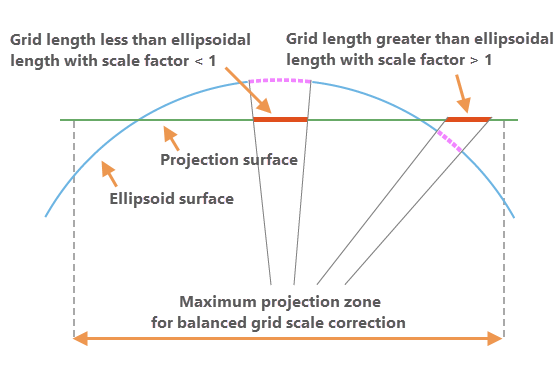
Grid scale factor
The grid scale factor converts distances between the geodetic distances on the ellipsoid surface and the grid plane of the projection. This factor is computed from the x,y location of the point and the properties of the projection surface.
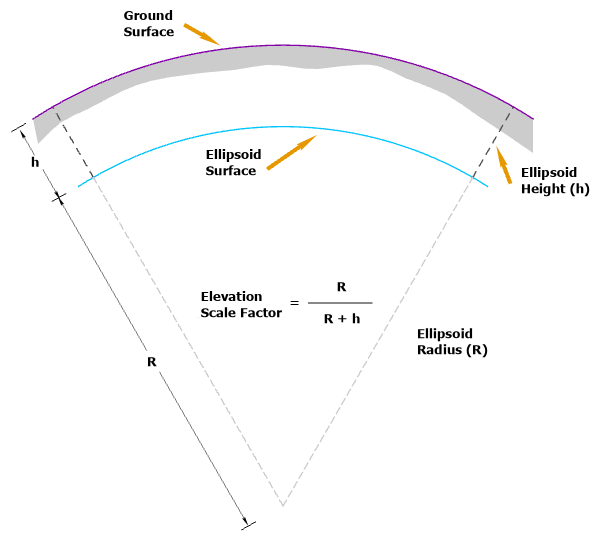
Elevation factor
The elevation factor converts distances between the geodetic distances on the ellipsoid surface and the horizontal ground distances. This factor is computed from the z-elevation of the point.
Combined scale factor
The applied distance factor value is calculated as a combined scale factor using grid scale and elevation factors. The combined scale factor is the product of multiplying the grid scale factor and the elevation factor.
These two scale factors correct the combined linear distortions caused by the curvature of the earth and the ground height of the measured distances above the ellipsoid surface with respect to the projection surface.