| Map projection | Example | Description |
|---|---|---|
| This projection shows the world in a square. It is a conformal projection except in the four corners of the square. | |
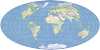
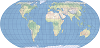
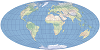
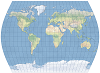
| This compromise modified azimuthal projection takes the form of an ellipse. It is used primarily for world maps. | |
| This equal-area conic projection is best suited for land masses extending in an east-to-west orientation at mid-latitudes. | |
| This compromise map projection adjusts the parallels to the height-to-width (aspect) ratio of a canvas. The aspect ratio must be between 0.3 and 1. | |
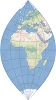
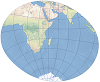
| The projection preserves both distance and direction from the central point. It is used primarily for hemisphere maps. | |
| This is a cylindrical equal-area projection with standard parallels at 30° north and south. | |
| This interrupted projection takes a form of a star, and it is used by the American Association of Geographers (AAG) in their logo. | |
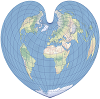
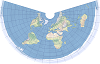
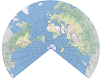
| This equal-area projection was historically used to map continents. Its graticule takes the form of a heart. | |
| This transverse cylindrical equidistant projection is appropriate for large-scale maps with predominantly north-to-south extent. | |
| This compromise cylindrical world map projection compresses polar areas in comparison to the Miller projection. | |
| This pseudocylindrical equal-area projection is primarily used for thematic maps of the world. | |
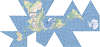
| This is a faceted projection consisting of six square sides that can be folded into a cube. | |
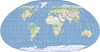
| This projection maintains the relative area on a map and presents the world as a rectangle. | |
| This azimuthal projection is conformal and used for large-scale coordinate systems in New Brunswick and the Netherlands. | |
| This compromise pseudocylindrical projection is primarily used as a novelty map. | |
| This equal area pseudocylindrical projection is primarily used as a novelty map. | |
| This is a compromise pseudocylindrical map projection used for general world maps. | |
| This equal-area pseudocylindrical map projection is commonly used for thematic and other world maps requiring accurate areas. | |
| This is a compromise pseudocylindrical map projection used for general world maps. | |
| This equal-area projection is used primarily for thematic world maps. | |
| This equal-area projection is a modification of the Lambert azimuthal equal-area projection. | |
| This equal-area pseudocylindrical projection has a pleasing appearance for land features and is used for thematic world maps. | |
| This conic projection preserves distances along all meridians and two standard parallels and is best suited for areas extending east to west at mid-latitudes. | |
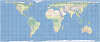
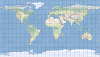
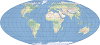
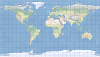
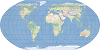
| This projection forms a grid of equal rectangles. It is also known as equirectangular, simple cylindrical, rectangular, and plate carrée. | |
| This projection is an unfolded 20-sided icosahedron that keeps the land masses unbroken. | |
| This perspective cylindrical map projection has two standard parallels at latitudes 45° north and 45° south and exaggerates polar regions. | |
| This projection is known as the ellipsoidal version of the transverse Mercator projection. It is a conformal projection that does not maintain true direction and is appropriate for mapping large-scale or smaller areas. | |
| This projection is used by geostationary satellites that return data located by the satellites' scanning angles. | |
| This azimuthal projection uses the center of the earth as its perspective point. It projects great circles as straight lines. | |
| This equal-area pseudocylindrical projection is combination of the Mollweide and sinusoidal projections, most commonly used in interrupted form. | |
| This projection is a modification of the Lambert azimuthal equal-area projection. It is also known as the Hammer-Aitoff. | |
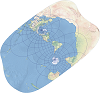
| This is an oblique Mercator projection developed by Martin Hotine. It is used for conformal mapping of areas that do not follow a north-south or east-west orientation but are obliquely oriented. | |
| This projection is used for urban maps in Colombia. This projection only supports very large scales. | |
| This is an oblique Lambert conformal conic projection designed for the former Czechoslovakia. It is used for areas that do not follow a north-south or east-west orientation but are obliquely oriented. | |
| This is an oblique Mercator projection developed by Jean Laborde. It is used for conformal mapping of areas that do not follow a north-south or east-west orientation but are obliquely oriented. | |
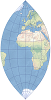
| This projection preserves land features at their true relative sizes. It is best suited for thematic hemisphere maps and thematic maps of polar regions. | |
| This conformal conic projection is best suited for land masses extending in an east-to-west orientation at mid-latitudes. | |
| This is a specialized map projection that does not take into account the curvature of the earth and can be used for local coordinate systems at very large scales. | |
| This projection shows loxodromes, or rhumb lines, as straight lines with the correct azimuth and scale from the intersection of the central meridian and the central parallel. | |
| This equal-area projection is used primarily for thematic world maps. | |
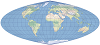
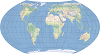
| This is a conformal cylindrical projection, originally created to display accurate compass bearings for sea travel. A feature of this projection is that all local shapes and angles are true at infinitesimal scale. | |
| This is similar to the Mercator projection except that the polar regions are not as distorted. | |
| This equal-area pseudocylindrical projection displays the world in the form of an ellipse with axes at a 2:1 ratio. This projection can be used for thematic small-scale maps. | |
| This is a compromise pseudocylindrical map projection for world maps. It was specifically designed for displaying physical data. | |
| This is a compromise pseudocylindrical map projection for world maps with distinguished meridians, which bend steeply toward the poles. | |
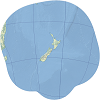
| This is the standard projection for large-scale maps of New Zealand. | |
 | This is a modified Lambert conformal conic projection used to map areas near the poles. | |
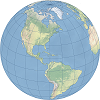
| This perspective projection views the globe from an infinite distance. This gives the illusion of a three-dimensional globe. | |
| This is a compromise cylindrical map projection designed by Tom Patterson in 2014. | |
| This projection shows the world as a square. It is a conformal projection except in the middle of the four sides of the square. | |
| This is a cylindrical map projection that can be constructed geometrically. A special case is the central cylindrical projection. | |
| This projection is simple to construct because it forms a grid of equal squares. This projection is often used to display data in a geographic coordinate system. | |
| The name of this projection translates to "many cones" and refers to the projection methodology. | |
| This pseudocylindrical equal-area projection is primarily used for thematic maps of the world. | |
| This is an oblique Mercator projection developed by Martin Hotine. It is used for conformal mapping of areas that do not follow a north-south or east-west orientation but are obliquely oriented. It is used in Malaysia and Brunei. | |
| This is a compromise projection used for world maps. | |
| This pseudocylindrical equal-area projection displays all parallels and the central meridian at true scale. | |
| This azimuthal projection is conformal. | |
| This compromise pseudocylindrical map projection is a modified Gall stereographic projection but with curved meridians. | |
| This projection is a compromise cylindrical map projection developed and introduced by Waldo Tobler in 1997 as his first simpler alternative to the Miller cylindrical projection. | |
| This projection is a compromise cylindrical map projection developed and introduced by Waldo Tobler in 1997 as his second simpler alternative to the Miller cylindrical projection. | |
| This projection is a transverse aspect of the cylindrical equal-area projection. This projection is appropriate for maps with a predominantly north-to-south extent. | |
| This is similar to the Mercator projection except that the cylinder is tangent along a meridian instead of the equator. The result is a conformal projection that does not maintain true direction and is appropriate for mapping large-scale or smaller areas. | |
| This modified azimuthal projection shows the true distance from either of two focal points to any other point on a map. | |
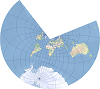
| This compromise polyconic projection shows the world as a circle. | |
| Unlike the orthographic projection, this perspective projection views the globe from a finite distance. This perspective gives the overall effect of the view from a satellite. | |
| This pseudocylindrical equal-area projection is used primarily for thematic world maps. | |
| This pseudocylindrical compromise projection is used primarily for world maps. | |
| This equal-area projection is a modification of the Lambert azimuthal equal-area projection. It is also known as the Hammer-Wagner projection and is primarily used for world thematic maps. | |
| This is a pseudocylindrical projection that averages the coordinates from the equidistant cylindrical and sinusoidal projections. | |
| This is a pseudocylindrical projection that averages the coordinates from the equidistant cylindrical and Mollweide projections. | |
| This is a compromise projection used for world maps that averages the coordinates from the equidistant cylindrical and Aitoff projections. This projection is used by the National Geographic Society for general world maps. |