Available with Geostatistical Analyst license.
While global polynomial interpolation fits a polynomial to the entire surface, local polynomial interpolation fits many polynomials, each within specified overlapping neighborhoods. The search neighborhood can be defined by using the size and shape, number of neighbors, and sector configuration. Alternatively, the Exploratory Trend Surface Analysis parameter can be used to simultaneously vary the Bandwidth, Spatial Condition Number (if enabled), and Searching Neighborhood values.
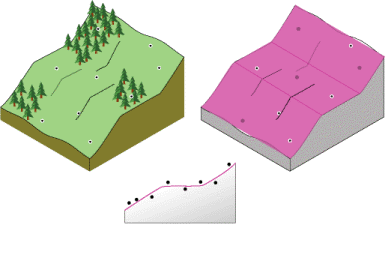
A first-order global polynomial fits a single plane through the data; a second-order global polynomial fits a surface with a bend in it, allowing surfaces representing valleys; a third-order global polynomial allows for two bends; and so forth. However, when a surface has a varying shape—such as a landscape that slopes, levels out, and slopes again—a single global polynomial will not fit well. Multiple polynomial planes would be able to represent the surface more accurately as shown in the following illustration:
Local polynomial interpolation, on the other hand, fits the specified order (zero, first, second, third, and so on) polynomial using points only within the defined neighborhood. The neighborhoods overlap, and the value used for each prediction is the value of the fitted polynomial at the center of the neighborhood.
In the following image, a cross section of sample elevation data is taken (a transect). In the first image, three neighbors (the red points) are used to fit a first-order polynomial and a line (the red line) to predict the unknown value for the location identified by the blue point. In the second image, a second location (the yellow point) is predicted by another first-order polynomial. It is very close to the first location, and the same measured points are used in the predictions, but the weights will be a little different, thus the polynomial fit (the blue line) is slightly different.


This process continues, centering on subsequent prediction locations, fitting local polynomials to predict the values. The two images below show two more arbitrary points being predicted to create the final surface. The orange point is predicted from the fitted polynomial (the green line) using the green measured sample points, and the brown point is predicted from the light purple polynomial.


In the two images below, two more polynomials are fit (the yellow and gray lines) to predict two more locations (the bluish-green and green points).


This process continues for each location. You can see how the surface is created (the purple surface line) for the sample points below.

Measures of accuracy
Local polynomial interpolation provides the following two measures of accuracy that are not available for the other deterministic interpolation methods offered in ArcGIS Geostatistical Analyst:
- Prediction standard errors indicate the uncertainty associated with the value predicted for each location.
- Spatial condition number is a measure of how stable or unstable the solution of the prediction equations is for a specific location. If the condition number is large, a small change in the matrix coefficients results in a large change in the solution vector (regression coefficients). The spatial condition number surface shows variation in the numerical model stability and provides additional information on the prediction uncertainty since the prediction standard error surface is created assuming that the model is correct.
Local polynomial interpolation will be most accurate when the data has the following properties:
- The samples were taken on a grid (that is, the samples are equally spaced).
- The data values, within the searching neighborhood, are normally distributed.
In practice, most datasets will not have these properties. In those cases, the predicted values will be affected, but not as much as the prediction standard errors. To help you decide if the results in certain areas are reliable or not, LPI provides a spatial condition number surface. Rule of thumb values are shown in the following table, and these critical values are rendered in yellow in the Condition Number surface:
| Order of polynomial | Critical spatial condition number threshold value |
|---|---|
1 | 10 |
2 | 100 |
3 | 1000 |
Greater than 3 | Not recommended for most situations |
Values that are below the critical spatial condition number thresholds indicate at which locations the solutions are reliable. Values close or equal to the critical values are questionable (should be examined with care), and values above the critical limits are not reliable.
The spatial condition numbers are generated by evaluating how sensitive the predicted value is to small changes in the coefficients of the linear prediction equations. A small spatial condition number indicates that the solution is stable, while a large value indicates that the solution is unstable. Instability of the solution should be a concern if it occurs in areas of particular interest, because small variations in the input data (including their values, locations, and spatial arrangement) can cause large variations in the predicted value. This means that any uncertainty associated with the input data (for example, errors in attribute measurements or imprecisions in the coordinates where the measurement was made) and especially the data outliers may have a considerable impact on the predicted values. Also, changes in the search neighborhood modify the number of data points (and weights in the case of a smooth search neighborhood) that are used to make a prediction and may affect the spatial condition number for that location.
The spatial condition number surface is created for the polynomials of order 1, 2, and 3. The prediction standard error is estimated assuming that the LPI model is correct (that is, the local weighted least squares regression is an adequate algorithm and the spatial condition number values are smaller than the spatial condition number threshold values in the table above).
You can exclude areas where high condition numbers occur in the prediction and prediction standard error maps by setting Use Spatial Condition Number Threshold to True on the LPI dialog box. The condition number is dependent only on the locations of the input points, not their actual values. In other words, whether the ozone or the elevation values coming from the same dataset are used as input to LPI, the condition number surface will remain the same.
In the case of regularly distributed data, Constant, Epanechnikov, and Quartic kernels are the best from a theoretical point of view for polynomials of order 0, 1, and 2 respectively. In the case of irregularly distributed data, selection of the best kernel should be based on the validation and cross-validation diagnostics and the spatial condition number values.
Kernel Interpolation with Barriers is a variant of LPI. Local instabilities in these results are corrected by using a technique that is similar to ridge regression. The trade-off is that the predicted values are slightly biased and in most practical situations, the bias is not enough to affect decisions that you make based on the predicted values.
Surface holes
If the Use Spatial Condition Number Threshold parameter is checked, there may be "holes" in the output surface. These are areas where the Spatial Condition Number Threshold is exceeded or the searching neighborhood is too small. The search neighborhood parameters and the Spatial Condition Number Threshold can be adjusted to fill-in these areas; however, it must be noted that these holes were created where there may be instability in the calculation of the prediction values.
When to use local polynomial interpolation
Global polynomial interpolation is useful for creating smooth surfaces and identifying long-range trends in the dataset. However, in earth sciences, the variable of interest usually has short-range variation in addition to long-range trend. When the dataset exhibits short-range variation, local polynomial interpolation maps can capture the short-range variation.
Local polynomial interpolation is sensitive to the neighborhood distance, and a small searching neighborhood may create empty areas in the prediction surface. For this reason, you can preview the surface before producing the output layer.