Available with Geostatistical Analyst license.
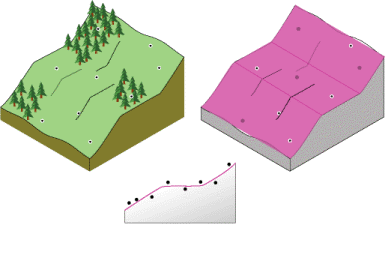
In Analyze the surface properties of nearby locations, interpolation that depends on distance is described. There are other solutions for predicting the values for unmeasured locations. For example, another proposed site for the observation area is on the face of a gently sloping hill. The face of the hill is a sloping plane. However, the locations of the samples are in slight depressions or on small mounds (local variation). Using the local neighbors to predict a location may overestimate or underestimate the prediction because of the influence of the depressions and mounds. Further, you may notice the local variation but not capture the overall sloping plane (referred to as the trend). The ability to identify and model local structures and surface trends can increase the accuracy of your predicted surface.
Local polynomial interpolation
What happens if the area you are interested in slopes, levels off, and slopes again? Fitting a flat plane through this study site would give poor predictions for the unmeasured values. However, if you are permitted to fit many smaller overlapping planes, and use the center of each plane as the prediction for each location in the study area, the resulting surface will be more flexible and perhaps more accurate. This is the conceptual basis for local polynomial interpolation.