Description
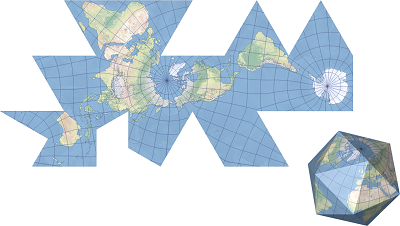
The Fuller map projection, also known as the Dymaxion map, converts the globe into a 20-sided figure called an icosahedron. Each side of that shape is a geodesic triangle that is then flattened into a two-dimensional triangle. The facets of the icosahedron are unfolded in a specific manner to keep the land masses unbroken.
The final version of this projection was described by Buckminster Fuller in 1954 after working on the map for several decades. For more information, refer to the Buckminster Fuller Institute website. The Fuller projection is available in ArcGIS Pro 1.0 and later and in ArcGIS Desktop 9.0 and later.
Projection properties
The subsections below describe the Fuller projection properties.
Graticule
Fuller is a faceted projection. All meridians and parallels are complex curves broken at the facet edges. None of the meridians and parallels follow any of the facet edges. Both poles project as points inside a facet.
Distortion
The Fuller projection is neither conformal nor equal-area. Shapes, areas, distances, directions, and angles are all generally distorted. Distortion increases as the distance from the facet edges increases. The scale is correct along the facet edges. Because the Fuller projection is comprised of 20 facets that are projected individually, overall distortion of the map is low.
Usage
The Fuller projection is intended only for representations of the entire globe. When presented as a flat map, the land masses are unbroken.
Limitations
The Fuller projection is supported on spheres only. For an ellipsoid, the semimajor axis is used for the radius. Some distortion properties are not maintained when an ellipsoid is used.
Parameters
Fuller parameters are as follows:
- False Easting
- False Northing
- Central Meridian
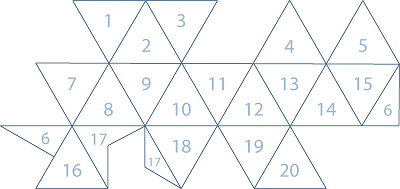
- Option, used to display the entire globe or just a single facet, as shown in the diagram below. Option = 0 results in the entire globe, all 20 facets displayed. This is the default.
Sources
Gray, R. W. (1994). "Fuller's DymaxionTM Map." Cartography and Geographic Information Systems, 21(4), p. 243-246
Gray, R. W. (1995). "Exact Transformation Equations For Fuller's World Map." Cartographica, 32(3), p. 17-25.
Snyder, J. P. (1993). Flattening the Earth. Two Thousand Years of Map Projections. Chicago and London: University of Chicago Press.