Example of 2D versus 3D results
Following is an example of the different results that occur when using Within a distance (WITHIN_A_DISTANCE in Python) or Within a distance 3D (WITHIN_A_DISTANCE_3D in Python) spatial relationships with 3D data. The Input Feature Layer is the rooms (purple cubes), and the Selecting Features is the small yellow circle. The operation is trying to answer the question Which rooms are within a distance of a specific x,y,z location (the yellow dot)? The result is quite different depending on which Relationship is used. If the Within a distance (WITHIN_A_DISTANCE in Python) relationship is used, all rooms within a distance (in the x- and y-coordinates only) are selected, so rooms from the bottom to the top floor are selected.
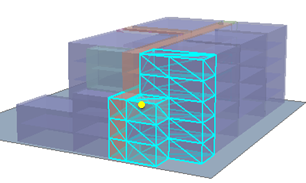
However, if the Within a distance 3D relationship is used, the measurement of distance between the x, y, z location (the yellow dot) and the individual rooms is calculated in three dimensions, resulting in only the rooms within a true 3D distance of the point being selected.

Valid input and selecting layers
Layers that meet one of the following criteria are valid as input and selecting layers:
- A layer from a feature class with the following geometry types: point, multipoint, line, multipatch, or polygon.
- A layer that uses a base height and/or extrusion.
- A layer that points to a layer file (.lyrx) that meets one of the above criteria is also valid. This can be useful when running an operation in a stand-alone Python script.
Get the best result
When using multipatches, the surface of the geometry is used when evaluating whether the 3D relationship is met, irrespective of whether or not the multipatch is closed. For example, when evaluating the 3D distance from a given point feature to a multipatch, such as a tetrahedron, the distance is calculated to the surface of the tetrahedron, irrespective of the point being contained inside the tetrahedron.
Using Within a distance 3D on data stored in an unprojected coordinate system (that is, data stored in a geographic coordinate system) may yield poor results due to the following:
- The conversion from decimal degrees to linear units is not consistent across large geographic extents.
- The global distances supported by the geographic coordinate system do not take into account the curvature of the surface of the earth (all measurements are done on a plane).