| Label | Explanation | Data Type |
Input Raster | The raster to be transformed. | Mosaic Layer; Raster Layer |
Source Control Points | The coordinates of the raster to be warped. | Point |
Target Control Points | The coordinates to which the source raster will be warped. | Point |
Output Raster Dataset | The name, location, and format for the dataset you are creating. When storing a raster dataset in a geodatabase, do not add a file extension to the name of the raster dataset. When storing your raster dataset to a JPEG file, JPEG 2000 file, TIFF file, or geodatabase, you can specify a compression type and compression quality. When storing the raster dataset in a file format, specify the file extension as follows:
| Raster Dataset |
Transformation Type (Optional) | Specifies the transformation method for shifting the raster dataset.
| String |
Resampling Technique (Optional) | Specifies the resampling technique that will be used. The default is Nearest. The Nearest and Majority options are used for categorical data, such as a land-use classification. The Nearest option is the default. It is the quickest and does not change the pixel values. Do not use either of these options for continuous data, such as elevation surfaces. The Bilinear and Cubic options are most appropriate for continuous data. It is recommended that you do not use either of these options with categorical data because the pixel values may be altered.
| String |
Summary
Transforms a raster dataset using source and target control points. This is similar to georeferencing.
Illustration
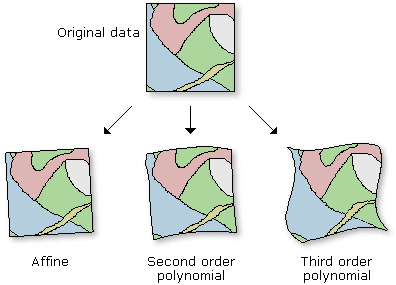
Usage
You must specify the source and target coordinates. The transformation type (polynomial order) from which to choose is dependent on the number of control points entered.
The default polynomial order will perform an affine transformation.
Warp is useful when the raster requires a systematic geometric correction that can be modeled with a polynomial. A spatial transformation can invert or remove a distortion using polynomial transformation of the proper order. The higher the order, the more complex the distortion that can be corrected. The higher orders of polynomial will involve progressively more processing time.
To determine the minimum number of links necessary for a given order of polynomial, use the following formula:
n = (p + 1) (p + 2) / 2where n is the minimum number of links required for a transformation of polynomial order p. It is recommended that you use more than the minimum number of links.
This tool will determine the extent of the warped raster and will set the number of rows and columns to be about the same as in the input raster. Some minor differences may be due to the changed proportion between the output raster's sizes in the x and y directions. The default cell size used will be computed by dividing the extent by the previously determined number of rows and columns. The value of the cell size will be used by the resampling algorithm.
If you choose to define an output cell size in the Environment settings, the number of rows and columns will be calculated as follows:
columns = (xmax - xmin) / cell size rows = (ymax - ymin) / cell sizeYou can save the output to BIL, BIP, BMP, BSQ, DAT, Esri Grid, GIF, IMG, JPEG, JPEG 2000, PNG, TIFF, MRF, or CRF format, or any geodatabase raster dataset.
When storing a raster dataset to a JPEG format file, a JPEG 2000 format file, or a geodatabase, you can specify a Compression Type value and a Compression Quality value in the geoprocessing environments.
This tool supports multidimensional raster data. To run the tool on each slice in the multidimensional raster and generate a multidimensional raster output, be sure to save the output to CRF.
Supported input multidimensional dataset types include multidimensional raster layer, mosaic dataset, image service, and CRF.
Parameters
arcpy.management.Warp(in_raster, source_control_points, target_control_points, out_raster, {transformation_type}, {resampling_type})| Name | Explanation | Data Type |
in_raster | The raster to be transformed. | Mosaic Layer; Raster Layer |
source_control_points [source_control_point,...] | The coordinates of the raster to be warped. | Point |
target_control_points [target_control_point,...] | The coordinates to which the source raster will be warped. | Point |
out_raster | The name, location, and format for the dataset you are creating. When storing a raster dataset in a geodatabase, do not add a file extension to the name of the raster dataset. When storing your raster dataset to a JPEG file, JPEG 2000 file, TIFF file, or geodatabase, you can specify a compression type and compression quality. When storing the raster dataset in a file format, specify the file extension as follows:
| Raster Dataset |
transformation_type (Optional) | Specifies the transformation method for shifting the raster dataset.
| String |
resampling_type (Optional) | Specifies the resampling technique that will be used. The default is Nearest.
The Nearest and Majority options are used for categorical data, such as a land-use classification. The Nearest option is the default. It is the quickest and does not change the pixel values. Do not use either of these options for continuous data, such as elevation surfaces. The Bilinear and Cubic options are most appropriate for continuous data. It is recommended that you do not use either of these options with categorical data because the pixel values may be altered. | String |
Code sample
This is a Python sample for the Warp tool.
import arcpy
arcpy.env.workspace = "c:/data"
source_pnt = "'234718 3804287';'241037 3804297';'244193 3801275'"
target_pnt = "'246207 3820084';'270620 3824967';'302634 3816147'"
arcpy.management.Warp("raster.img", source_pnt, target_pnt, "warp.tif", "POLYORDER1",
"BILINEAR")This is a Python script sample for the Warp tool.
##====================================
##Warp
import arcpy
arcpy.env.workspace = r"C:/Workspace"
##Warp a TIFF raster dataset with control points
##Define source control points
source_pnt = "'234718 3804287';'241037 3804297';'244193 3801275'"
##Define target control points
target_pnt = "'246207 3820084';'270620 3824967';'302634 3816147'"
arcpy.management.Warp("raster.img", source_pnt, target_pnt, "warp.tif", "POLYORDER2",
"BILINEAR")Environments
Licensing information
- Basic: Yes
- Standard: Yes
- Advanced: Yes