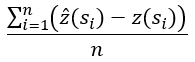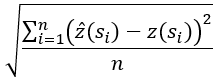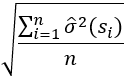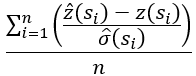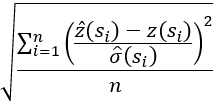| Label | Explanation | Data Type |
Input geostatistical layer | The geostatistical layer to be analyzed. | Geostatistical Layer |
Output point feature class (Optional) | Stores the cross-validation statistics at each location in the geostatistical layer. | Feature Class |
Derived Output
| Label | Explanation | Data Type |
| Count | Total number of samples used. | Long |
| Mean error | Mean Error—The averaged difference between the measured and the predicted values. | Double |
| Root mean square | Root Mean Square Error—Indicates how closely your model predicts the measured values. | Double |
| Average standard | Average Standard Error—The average of the prediction standard errors. | Double |
| Mean standardized | Mean Standardized Error—The average of the standardized errors. | Double |
| Root mean square standardized | Root Mean Square Standardized Error—This should be close to 1 if the prediction standard errors are valid. | Double |
| Percent in 90% Interval | Percent in 90% Interval—The percentage of points that are in a 90 percent cross-validation confidence interval. This value should be close to 90. | Double |
| Percent in 95% Interval | Percent in 95% Interval—The percentage of points that are in a 95 percent cross-validation confidence interval. This value should be close to 95. | Double |
| Average CRPS | Average CRPS—The average Continuous Ranked Probability Score (CRPS) of all points. The CRPS is a diagnostic that measures the deviation from the predictive cumulative distribution function to each observed data value. This value should be as small as possible. This diagnostic has advantages over other cross-validation diagnostics because it compares the data to a full distribution rather than to single-point predictions. The calculation of this statistic involves simulations so it cannot be written in a simple formula. | Double |