Available with Spatial Analyst license.
Legacy:
This functionality is deprecated and will be removed in a future release.
See Distance analysis and Migrate from legacy distance tools to distortion free distance tools for more information about the enhanced capabilities.
The focus of the Cost Connectivity tool is on defining the optimum network of least-cost paths, not on the creation of separate paths connecting one region to another region. On the resulting network, the phenomenon can move from one region to any other region using the paths (possibly traveling through other regions).
Example problems solved by cost connectivity
- From a suitability model, you have identified 10 of the best habitat patches for bobcat. You want the bobcats to move between the patches through the most effective network of wildlife corridors to maintain genetic diversity within the metapopulation.
- In a military peacekeeping deployment, you have identified 5 areas to position troops and personnel. You want to develop the best network of supply routes between the bases.
- In a timber harvest, you want to create the most cost-efficient network of logging roads from which to extract the lumber.
How the cost connectivity algorithm works
The following steps are conceptually how the Cost Connectivity algorithm works:
- The input sources and cost surface are identified.
In the graphic below, the input regions (the colored polygons) are displayed over the cost surface layer.
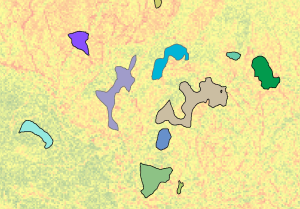
The input regions are displayed over the cost surface raster. - A Cost Allocation is performed.
In the graphic below, the input regions are displayed over the associated cost allocation layer. The value of each cell in the allocation raster is that of the particular region that can be reached with the cheapest (lowest) accumulated cost.
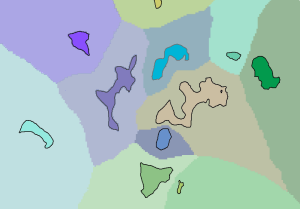
Regions displayed over cost allocation layer - Cost paths are created between each region and its neighboring cost region.
In the graphic below, the input regions and the least-cost paths from each region to its neighboring cost region (magenta lines) are displayed over the associated cost allocation layer.
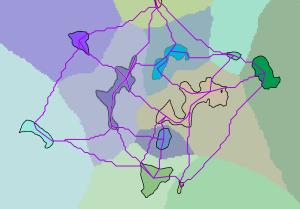
Cost allocation with regions connected by paths - The regions and the resulting paths are converted to a graph (in graph theory). In the translation, the regions are the vertices and the paths are the edges. The accumulative cost for the path is the weight for the edge.
Conceptually, the translation of the regions and paths into graph theory can be represented by the following illustration. The numbered circles are the vertices (the regions) and the connecting lines between the vertices are the edges (the least-cost paths). The weights for the edges are the accumulative cost for the paths. In the illustration, the higher the cost, the thicker the line.
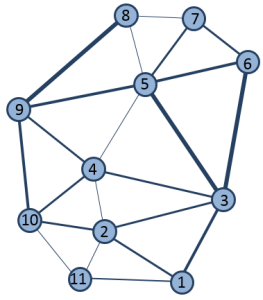
Conceptual illustration of graph theory Note:
To fully understand how this tool works, it is recommended that you have some basic understanding of graph theory. Many resources are available for this, but you can start with the Wikipedia entry at https://en.wikipedia.org/wiki/Graph_theory.
- The minimum spanning tree is determined using graph theory to connect the vertices (the regions) in the most effective (least cost) way possible.
Note:
More information about minimum spanning trees is available online, such as from the Wikipedia entry at https://en.wikipedia.org/wiki/Minimum_spanning_tree.
- The spatial representation of the regions and the paths from the minimum spanning tree are mapped back to an output feature class.
In the graphic below, the input regions and the least-cost path network from the minimum spanning tree (magenta color) are displayed over the associated cost surface layer.
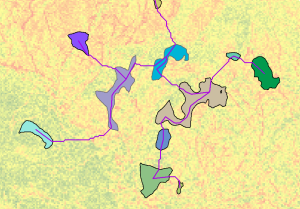
Output paths between regions displayed over the cost raster - Optionally, a feature class of the paths to the neighboring cost regions can be output (see step 3, above).
Each path will be a separate linear feature and there will be duplicate lines where the corridors travel a common segment.
If the input regions are polygons, the paths are continued to a point within the polygon to allow the traveler to enter by one path, move within the region, and exit by another path to reach a distant region. No cost is assigned to these extended segments within a region; therefore, there is no cost to move within the region. The same is the case for linear regions—there is no cost to move along the linear feature to reach another path.
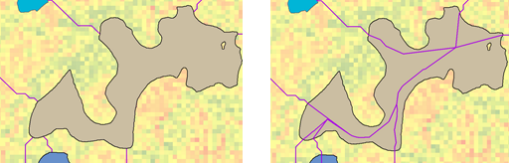
In the graphic below, the left side is the result from using the Cost Distance and Cost Path sequence of tools to connect regions. Notice the paths reach only to the edge of the regions. The right image shows the resulting network of paths connecting the regions from Cost Connectivity. Notice that the paths continue within the region, allowing the traveler to enter the region by one path and leave by another.
The importance of regions
The input to Cost Connectivity must be regions. A region is a connected series of cells (adjacent) with the same value. If you have disconnected cells with the same value, then these are zones. Zones can be converted to regions using the Region Group tool. Cost Connectivity connects every region to every other region, so all regions, and all cells in the regions, can be reached through the resulting network.
The cost connectivity workflow scenarios
The following are common scenarios for using the Cost Connectivity tool.
- The optimum network (the minimum spanning tree) is the desired output.
- Add specific paths to the optimum network using Cost Distance and Cost Path to connect regions for reasons that the optimum network does not capture. For example, adding an escape trail for fire fighters to flee a raging fire.
- Create the desired network from the optional output of all paths to the neighboring regions by using expert knowledge to remove unnecessary paths.
- Turn any of the above scenarios into a Network Analyst network and perform additional analysis of the movement between the regions.