| Label | Explanation | Data Type |
Input Features | The feature class or feature layer containing the dependent and candidate explanatory variables to analyze. | Feature Layer |
Dependent Variable | The numeric field containing the observed values you want to model using OLS. | Field |
Candidate Explanatory Variables | A list of fields to try as OLS model explanatory variables. | Field |
Weights Matrix File
(Optional) | A file containing spatial weights that define the spatial relationships among your input features. This file is used to assess spatial autocorrelation among regression residuals. You can use the Generate Spatial Weights Matrix File tool to create this. When you do not provide a spatial weights matrix file, residuals are assessed for spatial autocorrelation based on each feature's 8 nearest neighbors. Note: The spatial weights matrix file is only used to analyze spatial structure in model residuals; it is not used to build or to calibrate any of the OLS models. | File |
Output Report File (Optional) | The report file contains tool results, including details about any models found that passed all the search criteria you entered. This output file also contains diagnostics to help you fix common regression problems in the case that you don't find any passing models. | File |
Output Results Table
(Optional) | The optional output table created containing the explanatory variables and diagnostics for all of the models within the Coefficient p-value and VIF value cutoffs. | Table |
Maximum Number of Explanatory Variables (Optional) | All models with explanatory variables up to the value entered here will be assessed. If, for example, the Minimum Number of Explanatory Variables is 2 and the Maximum Number of Explanatory Variables is 3, the Exploratory Regression tool will try all models with every combination of two explanatory variables, and all models with every combination of three explanatory variables. | Long |
Minimum Number of Explanatory Variables (Optional) | This value represents the minimum number of explanatory variables for models evaluated. If, for example, the Minimum Number of Explanatory Variables is 2 and the Maximum Number of Explanatory Variables is 3, the Exploratory Regression tool will try all models with every combination of two explanatory variables, and all models with every combination of three explanatory variables. | Long |
Minimum Acceptable Adj R Squared
(Optional) | This is the lowest Adjusted R-Squared value you consider a passing model. If a model passes all of your other search criteria, but has an Adjusted R-Squared value smaller than the value entered here, it will not show up as a Passing Model in the Output Report File. Valid values for this parameter range from 0.0 to 1.0. The default value is 0.05, indicating that passing models will explain at least 50 percent of the variation in the dependent variable. | Double |
Maximum Coefficient p value Cutoff
(Optional) | For each model evaluated, OLS computes explanatory variable coefficient p-values. The cutoff p-value you enter here represents the confidence level you require for all coefficients in the model in order to consider the model passing. Small p-values reflect a stronger confidence level. Valid values for this parameter range from 1.0 down to 0.0, but will most likely be 0.1, 0.05, 0.01, 0.001, and so on. The default value is 0.05, indicating passing models will only contain explanatory variables whose coefficients are statistically at the 95 percent confidence level (p-values smaller than 0.05). To relax this default you would enter a larger p-value cutoff, such as 0.1. If you are getting lots of passing models, you will likely want to make this search criteria more stringent by decreasing the default p-value cutoff from 0.05 to 0.01 or smaller. | Double |
Maximum VIF Value Cutoff
(Optional) | This value reflects how much redundancy (multicollinearity) among model explanatory variables you will tolerate. When the VIF (Variance Inflation Factor) value is higher than about 7.5, multicollinearity can make a model unstable; consequently, 7.5 is the default value here. If you want your passing models to have less redundancy, you would enter a smaller value, such as 5.0, for this parameter. | Double |
Minimum Acceptable Jarque Bera p value
(Optional) | The p-value returned by the Jarque-Bera diagnostic test indicates whether the model residuals are normally distributed. If the p-value is statistically significant (small), the model residuals are not normal and the model is biased. Passing models should have large Jarque-Bera p-values. The default minimum acceptable p-value is 0.1. Only models returning p-values larger than this minimum will be considered passing. If you are having trouble finding unbiased passing models, and decide to relax this criterion, you might enter a smaller minimum p-value such as 0.05. | Double |
Minimum Acceptable Spatial Autocorrelation p value
(Optional) | For models that pass all of the other search criteria, the Exploratory Regression tool will check model residuals for spatial clustering using Global Moran's I. When the p-value for this diagnostic test is statistically significant (small), it indicates the model is very likely missing key explanatory variables (it isn't telling the whole story). Unfortunately, if you have spatial autocorrelation in your regression residuals, your model is misspecified, so you cannot trust your results. Passing models should have large p-values for this diagnostic test. The default minimum p-value is 0.1. Only models returning p-values larger than this minimum will be considered passing. If you are having trouble finding properly specified models because of this diagnostic test, and decide to relax this search criteria, you might enter a smaller minimum such as 0.05. | Double |
Summary
Evaluates all possible combinations of the input candidate explanatory variables, looking for OLS models that best explain the dependent variable within the context of user-specified criteria.
Illustration
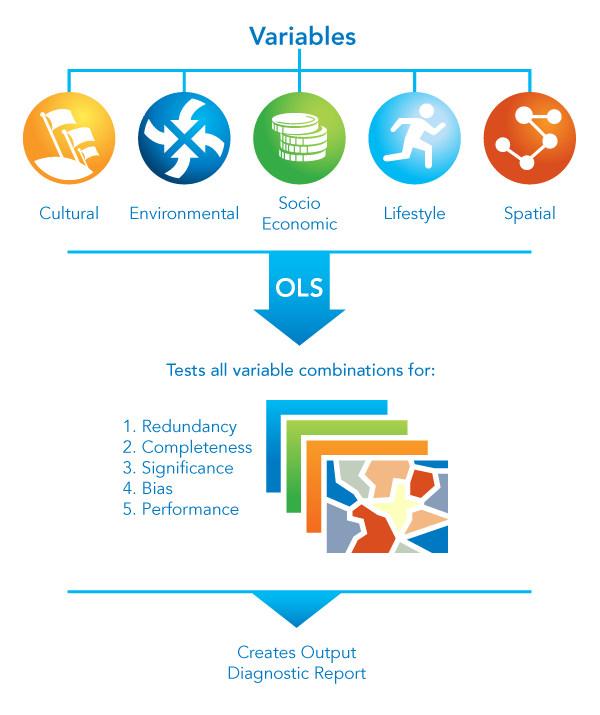
Usage
The primary output for this tool is a report file which is written as messages at the bottom of the Geoprocessing pane during tool execution. You may access the messages by hovering over the progress bar, clicking on the pop-out button, or expanding the messages section in the Geoprocessing pane. You may also access the messages for a previous run of Exploratory Regression via the Geoprocessing History.
This tool will optionally create a text file report summarizing results. This report file will be added to the table of contents (TOC) and may be viewed in ArcMap by right-clicking on it and selecting Open.
This tool also produces an optional table of all models meeting your maximum coefficient p-value cutoff and Variance Inflation Factor (VIF) value criteria. A full explanation of the report elements and table is provided in Interpreting Exploratory Regression Results.
This tool uses Ordinary Least Squares (OLS) and Spatial Autocorrelation (Global Moran's I). The optional spatial weights matrix file is used with the Spatial Autocorrelation (Global Moran's I) tool to assess model residuals; it is not used by the OLS tool at all.
This tool tries every combination of the Candidate Explanatory Variables entered, looking for a properly specified OLS model. Only when it finds a model that meets your threshold criteria for Minimum Acceptable Adj R Squared, Maximum Coefficient p-value Cutoff, Maximum VIF Value Cutoff and Minimum Acceptable Jarque-Bera p-value will it run the Spatial Autocorrelation (Global Moran's I) tool on the model residuals to see if the under/over-predictions are clustered or not. In order to provide at least some information about residual clustering in the case where none of the models pass all of these criteria, the Spatial Autocorrelation (Global Moran's I) test is also applied to the residuals for the three models that have the highest Adjusted R2 values and the three models that have the largest Jarque-Bera p-values.
Especially when there is strong spatial structure in your dependent variable, you will want to try to come up with as many candidate spatial explanatory variables as you can. Some examples of spatial variables would be distance to major highways, accessibility to job opportunities, number of local shopping opportunities, connectivity measurements, or densities. Until you find explanatory variables that capture the spatial structure in your dependent variable, model residuals will likely not pass the spatial autocorrelation test. Significant clustering in regression residuals, as determined by the Spatial Autocorrelation (Global Moran's I) tool, indicates model misspecification. Strategies for dealing with misspecification are outlined in What they don't tell you about regression analysis.
Because the Spatial Autocorrelation (Global Moran's I) is not run for all of the models tested (see the previous usage tip), the optional Output Results Table will have missing data for the SA (Spatial Autocorrelation) field. Because DBF (.dbf) files do not store null values, these appear as very, very small (negative) numbers (something like -1.797693e+308). For geodatabase tables, these missing values appear as null values. A missing value indicates that the residuals for the associated model were not tested for spatial autocorrelation because the model did not pass all of the other model search criteria.
The default spatial weights matrix file used to run the Spatial Autocorrelation (Global Moran's I) tool is based on an 8 nearest neighbor conceptualization of spatial relationships. This default was selected primarily because it executes fairly quickly. To define neighbor relationships differently, however, you can simply create your own spatial weights matrix file using the Generate Spatial Weights Matrix File tool, then specify the name of that file for the Input Spatial Weights Matrix File parameter. Inverse Distance, Polygon Contiguity, or K Nearest Neighbors, are all appropriate Conceptualizations of Spatial Relationships for testing regression residuals.
Note:
The spatial weights matrix file is only used to test model residuals for spatial structure. When a model is properly specified, the residuals are spatially random (large residuals are intermixed with small residuals; large residuals do not cluster together spatially).
Note:
When there are 8 or less features in the Input Features, the default spatial weights matrix file used to run the Spatial Autocorrelation (Global Moran's I) tool is based on K nearest neighbors where K is the number of features minus 2. In general, you will want to have a minimum of 30 features when you use this tool.
Parameters
arcpy.stats.ExploratoryRegression(Input_Features, Dependent_Variable, Candidate_Explanatory_Variables, {Weights_Matrix_File}, {Output_Report_File}, {Output_Results_Table}, {Maximum_Number_of_Explanatory_Variables}, {Minimum_Number_of_Explanatory_Variables}, {Minimum_Acceptable_Adj_R_Squared}, {Maximum_Coefficient_p_value_Cutoff}, {Maximum_VIF_Value_Cutoff}, {Minimum_Acceptable_Jarque_Bera_p_value}, {Minimum_Acceptable_Spatial_Autocorrelation_p_value})| Name | Explanation | Data Type |
Input_Features | The feature class or feature layer containing the dependent and candidate explanatory variables to analyze. | Feature Layer |
Dependent_Variable | The numeric field containing the observed values you want to model using OLS. | Field |
Candidate_Explanatory_Variables [Candidate_Explanatory_Variables,...] | A list of fields to try as OLS model explanatory variables. | Field |
Weights_Matrix_File (Optional) | A file containing spatial weights that define the spatial relationships among your input features. This file is used to assess spatial autocorrelation among regression residuals. You can use the Generate Spatial Weights Matrix File tool to create this. When you do not provide a spatial weights matrix file, residuals are assessed for spatial autocorrelation based on each feature's 8 nearest neighbors. Note: The spatial weights matrix file is only used to analyze spatial structure in model residuals; it is not used to build or to calibrate any of the OLS models. | File |
Output_Report_File (Optional) | The report file contains tool results, including details about any models found that passed all the search criteria you entered. This output file also contains diagnostics to help you fix common regression problems in the case that you don't find any passing models. | File |
Output_Results_Table (Optional) | The optional output table created containing the explanatory variables and diagnostics for all of the models within the Coefficient p-value and VIF value cutoffs. | Table |
Maximum_Number_of_Explanatory_Variables (Optional) | All models with explanatory variables up to the value entered here will be assessed. If, for example, the Minimum_Number_of_Explanatory_Variables is 2 and the Maximum_Number_of_Explanatory_Variables is 3, the Exploratory Regression tool will try all models with every combination of two explanatory variables, and all models with every combination of three explanatory variables. | Long |
Minimum_Number_of_Explanatory_Variables (Optional) | This value represents the minimum number of explanatory variables for models evaluated. If, for example, the Minimum_Number_of_Explanatory_Variables is 2 and the Maximum_Number_of_Explanatory_Variables is 3, the Exploratory Regression tool will try all models with every combination of two explanatory variables, and all models with every combination of three explanatory variables. | Long |
Minimum_Acceptable_Adj_R_Squared (Optional) | This is the lowest Adjusted R-Squared value you consider a passing model. If a model passes all of your other search criteria, but has an Adjusted R-Squared value smaller than the value entered here, it will not show up as a Passing Model in the Output_Report_File. Valid values for this parameter range from 0.0 to 1.0. The default value is 0.5, indicating that passing models will explain at least fifty percent of the variation in the dependent variable. | Double |
Maximum_Coefficient_p_value_Cutoff (Optional) | For each model evaluated, OLS computes explanatory variable coefficient p-values. The cutoff p-value you enter here represents the confidence level you require for all coefficients in the model in order to consider the model passing. Small p-values reflect a stronger confidence level. Valid values for this parameter range from 1.0 down to 0.0, but will most likely be 0.1, 0.05, 0.01, 0.001, and so on. The default value is 0.05, indicating passing models will only contain explanatory variables whose coefficients are statistically at the 95 percent confidence level (p-values smaller than 0.05). To relax this default you would enter a larger p-value cutoff, such as 0.1. If you are getting lots of passing models, you will likely want to make this search criteria more stringent by decreasing the default p-value cutoff from 0.05 to 0.01 or smaller. | Double |
Maximum_VIF_Value_Cutoff (Optional) | This value reflects how much redundancy (multicollinearity) among model explanatory variables you will tolerate. When the VIF (Variance Inflation Factor) value is higher than about 7.5, multicollinearity can make a model unstable; consequently, 7.5 is the default value here. If you want your passing models to have less redundancy, you would enter a smaller value, such as 5.0, for this parameter. | Double |
Minimum_Acceptable_Jarque_Bera_p_value (Optional) | The p-value returned by the Jarque-Bera diagnostic test indicates whether the model residuals are normally distributed. If the p-value is statistically significant (small), the model residuals are not normal and the model is biased. Passing models should have large Jarque-Bera p-values. The default minimum acceptable p-value is 0.1. Only models returning p-values larger than this minimum will be considered passing. If you are having trouble finding unbiased passing models, and decide to relax this criterion, you might enter a smaller minimum p-value such as 0.05. | Double |
Minimum_Acceptable_Spatial_Autocorrelation_p_value (Optional) | For models that pass all of the other search criteria, the Exploratory Regression tool will check model residuals for spatial clustering using Global Moran's I. When the p-value for this diagnostic test is statistically significant (small), it indicates the model is very likely missing key explanatory variables (it isn't telling the whole story). Unfortunately, if you have spatial autocorrelation in your regression residuals, your model is misspecified, so you cannot trust your results. Passing models should have large p-values for this diagnostic test. The default minimum p-value is 0.1. Only models returning p-values larger than this minimum will be considered passing. If you are having trouble finding properly specified models because of this diagnostic test, and decide to relax this search criteria, you might enter a smaller minimum such as 0.05. | Double |
Code sample
The following Python window script demonstrates how to use the ExploratoryRegression function.
import arcpy
arcpy.env.workspace = r"C:\ER"
arcpy.stats.ExploratoryRegression(
"911CallsER.shp", "Calls",
["Pop", "Jobs", "LowEduc", "Dst2UrbCen", "Renters", "Unemployed",
"Businesses", "NotInLF", "ForgnBorn", "AlcoholX", "PopDensity",
"MedIncome", "CollGrads", "PerCollGrd", "PopFY", "JobsFY", "LowEducFY"],
"BG_911Calls.swm", "BG_911Calls.txt", "", "MAX_NUMBER_ONLY", "5", "1",
"0.5", "0.05", "7.5", "0.1", "0.1")The following stand-alone Python script demonstrates how to use the ExploratoryRegression function.
# Exploratory Regression of 911 calls in a metropolitan area
# using the Exploratory Regression tool.
# Import system modules.
import arcpy
# Set property to overwrite existing output, by default.
arcpy.env.overwriteOutput = True
# Set the current workspace (to avoid having to specify the full path to the
# feature classes each time).
arcpy.env.workspace = r"C:\ER"
# Join the 911 Call Point feature class to the Block Group Polygon feature
# class.
# Process: Spatial Join
fieldMappings = arcpy.FieldMappings()
fieldMappings.addTable("BlockGroups.shp")
fieldMappings.addTable("911Calls.shp")
sj = arcpy.analysis.SpatialJoin(
"BlockGroups.shp", "911Calls.shp", "BG_911Calls.shp", "JOIN_ONE_TO_ONE",
"KEEP_ALL", fieldMappings, "COMPLETELY_CONTAINS")
# Delete extra fieldsto clean up the data
# Process: Delete Field
arcpy.management.DeleteField(
"BG_911Calls.shp",
["OBJECTID", "INC_NO", "DATE_", "MONTH_", "STIME", "SD_T", "DISP_REC"
"NFPA_TYP", "CALL_TYPE", "RESP_COD", "NFPA_SF", "SIT_FND", "FMZ_Q", "FMZ",
"RD", "JURIS", "COMPANY", "COMP_COD", "RESP_YN", "DISP_DT", "DAY_", "D1_N2",
"RESP_DT", "ARR_DT", "TURNOUT", "TRAVEL", "RESP_INT", "ADDRESS_ID", "ITY",
"CO", "AV_STATUS", "AV_SCORE", "AV_SIDE", "Season", "DayNight"])
# Create Spatial Weights Matrix for Calculations.
# Process: Generate Spatial Weights Matrix
swm = arcpy.stats.GenerateSpatialWeightsMatrix(
"BG_911Calls.shp", "TARGET_FID", "BG_911Calls.swm", "CONTIGUITY_EDGES_CORNERS",
"EUCLIDEAN", "1", "", "", "ROW_STANDARDIZATION")
# Exploratory Regression Analysis for 911 Calls.
# Process: Exploratory Regression
er = arcpy.stats.ExploratoryRegression(
"BG_911Calls.shp", "Calls",
["Pop", "Jobs", "LowEduc", "Dst2UrbCen", "Renters", "Unemployed",
"Businesses", "NotInLF", "ForgnBorn", "AlcoholX", "PopDensity",
"MedIncome", "CollGrads", "PerCollGrd", "PopFY", "JobsFY", "LowEducFY"],
"BG_911Calls.swm", "BG_911Calls.txt", "",
"MAX_NUMBER_ONLY", "5", "1", "0.5", "0.05", "7.5", "0.1", "0.1")Environments
Licensing information
- Basic: Yes
- Standard: Yes
- Advanced: Yes
Related topics
- An Overview of the Modeling Spatial Relationships toolset
- Find a geoprocessing tool
- How Geographically Weighted Regression works
- How Exploratory Regression works
- Regression analysis basics
- What they don't tell you about regression analysis
- Interpreting Exploratory Regression results
- Geographically Weighted Regression (GWR)
- Spatial Autocorrelation (Global Moran's I)
- What is a z-score? What is a p-value?
- How OLS regression works