Disponible con una licencia de Spatial Analyst.
Disponible con una licencia de 3D Analyst.
La herramienta Orientación identifica la dirección de la pendiente descendente. Los valores de cada celda del ráster de salida indican la dirección de brújula a la que apunta la superficie en esa ubicación. Se mide en el sentido de las agujas del reloj en grados de 0 (hacia el norte) a 360 (hacia el norte, nuevamente), formando un círculo completo. Las áreas planas que no tienen dirección de pendiente descendente tienen un valor de -1.
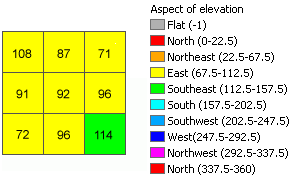
En las imágenes siguientes se muestra un dataset de elevación de entrada y el ráster de orientación de salida.
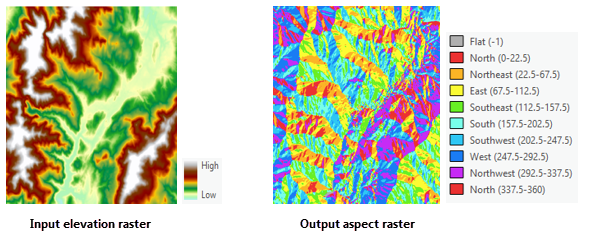
¿Por qué debo usar la herramienta Orientación?
Con la herramienta Orientación, puede hacer lo siguiente:
- Buscar todas las pendientes mirando al norte en una montaña, como parte de una búsqueda de las mejores pendientes para hacer esquí.
- Calcular la iluminación solar para cada ubicación de una región como parte de un estudio para determinar la diversidad de vida en cada sitio.
- Buscar todas las pendientes hacia el sur en una región montañosa para identificar las ubicaciones donde es posible que la nieve se derrita primero, como parte de un estudio para identificar las ubicaciones residenciales que son propensas a ser afectadas primero por la escorrentía.
- Identificar áreas de terreno plano para descubrir un área en donde pueda aterrizar un aeroplano en caso de emergencia.
Métodos de cálculo y el efecto del borde
Para calcular la orientación hay dos métodos disponibles. Puede elegir entre realizar cálculos Planares o Geodésicos con el parámetro de Método.
Con el método planar, el cálculo se realizará en un plano liso proyectado utilizando un sistema de coordenadas cartesianas 2D. Con el método geodésico, el cálculo se realizará en un sistema de coordenadas cartesianas 3D teniendo en cuenta la forma de la Tierra como un elipsoide.
Tanto los cálculos planares como geodésicos se realizan utilizando una vecindad de celdas de 3 x 3 (ventana móvil). Para cada vecindad, si la celda de procesamiento (central) es NoData, la salida es no NoData. El cálculo también requiere que al menos siete celdas vecinas a la celda de procesamiento sean válidas. Si hay menos de siete celdas válidas, el cálculo no se realizará y la salida en esa celda de procesamiento será NoData.
Las celdas de las filas y columnas más exteriores del ráster de salida serán NoData. Esto se debe a que esas celdas no tienen suficientes vecinos válidos a lo largo del límite del dataset de entrada.
Método planar
El método planar es el método tradicional para calcular la orientación.
Algoritmo de orientación planar
Una ventana de 3 x 3 móvil visita cada celda del ráster de entrada y, para cada celda en el centro de la ventana, se calcula un valor de orientación mediante un algoritmo que incorpora los valores de las ocho vecinas de la celda. Las celdas se identifican como letras, de la a a la i, con la letra e representando la celda para la cual se calcula la orientación.
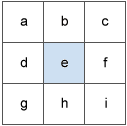
La tasa de cambio en la dirección x de la celda e se calcula con el siguiente algoritmo:
[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / 8- donde:
wght1 y wght2 son los recuentos ponderados horizontales de las celdas válidas.
Por ejemplo:
- si c, f e i tienen valores válidos, wght1 = (1+2*1+1) = 4.
- si i es NoData, wght1 = (1+2*1+0) = 3.
- si f es NoData, wght1 = (1+2*0+1) = 2.
Se aplica una lógica similar a wght2, salvo que las ubicaciones vecinas sean a, d y g.
La tasa de cambio en la dirección y de la celda e se calcula con el siguiente algoritmo:
[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4 ) / 8- donde:
wght3 y wght4 son el mismo concepto que en cálculo de [dz/dx].
Tomando la tasa de cambio en la dirección x e y de la celda e, la orientación se calcula utilizando:
orientación = 57.29578 * atan2 ([dz/dy], -[dz/dx])El valor de orientación después se convierte a valores de dirección de brújula (de 0 a 360 grados), de acuerdo a la siguiente regla:
if aspect < 0 cell = 90.0 - aspect>
else if aspect > 90.0 cell = 360.0 - aspect + 90.0 else cell = 90.0 - aspectEjemplo de cálculo de orientación planar
En este ejemplo, se calcula el valor de la orientación planar de la celda central de la ventana móvil.
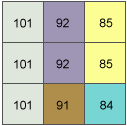
La tasa de cambio en la dirección x de la celda central e es:
[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / 8 = ((85 + 170 + 84)*4/(1+2+1) - (101 + 202 + 101)*4/(1+2+1)) / 8 = -8.125La tasa de cambio en la dirección y de la celda e es:
[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4) / 8 = ((101 + 182 + 84)*4/(1+2+1) - (101 + 184 + 85)*4/(1+2+1)) / 8 = -0.375La orientación se calcula como:
aspect = 57.29578 * atan2 ([dz/dy], -[dz/dx]) = 57.29578 * atan2 (-0.375, 8.125) = -2.64Como el valor calculado es menor que cero, la regla final se aplicará como:
cell = 90.0 - aspect = 90 - (-2.64) = 90 + 2.64 = 92.64El valor de 92,64 de la celda central e indica que su orientación está en la dirección este.
Método geodésico
El método geodésico mide la orientación de la superficie en un sistema de coordenadas 3D geocéntricas, también llamado sistema de coordenadas centrado en la Tierra, Tierra fija (ECEF), teniendo en cuenta la forma de la Tierra como un elipsoide. La forma en que esté proyectado el dataset no afectará al resultado del cálculo. Se utilizarán las unidades z del ráster de entrada si están definidas en la referencia espacial. Si la referencia espacial de la entrada no define las unidades z, deberá hacerlo con el parámetro de unidad z. El método geodésico produce una orientación más exacta que el método planar.
Transformación de coordenadas geodésicas
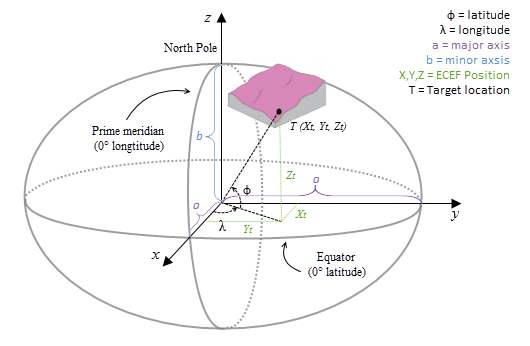
El sistema de coordenadas de ECEF es un sistema de coordenadas cartesianas dextrógiro 3D cuyo origen es el centro de la Tierra, donde cualquier ubicación se representa mediante coordenadas X, Y y Z. Consulte la figura siguiente para ver un ejemplo de una ubicación de destino T expresada con coordenadas geocéntricas.
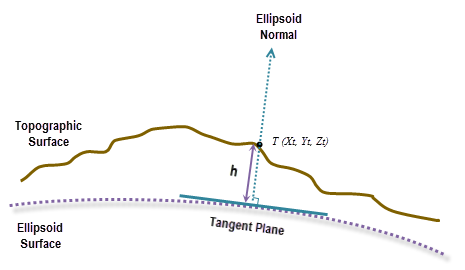
El cálculo geodésico utiliza una coordenada X, Y, Z que se calcula según sus coordenadas geodésicas (latitud φ, longitud λ, altura h). Si el sistema de coordenadas del ráster de superficie de entrada es un sistema de coordenadas proyectadas (PCS), el ráster se reproyecta primero a un sistema de coordenadas geográficas (GCS) donde cada ubicación tiene una coordenada geodésica y, a continuación, se transforma en el sistema de coordenadas de ECEF. La altura h (valor z) es la altura de elipsoide asociada a la superficie de elipsoide. Consulte el gráfico de la ilustración a continuación.
Para transformar a coordenadas de ECEF desde una coordenada geodésica (latitud φ, longitud λ, altura h), utilice las fórmulas siguientes:
X = (N(φ)+h)cosφcosλY = (N(φ)+h)cosφsinλZ = (b2/a2*N(φ)+h)sinφ- donde:
- N( φ ) = a2/ √(a2cosφ2+b2sinφ2)
- φ = latitud
- λ = longitud
- h = altura de elipsoide
- a = eje mayor del elipsoide
- b = eje menor del elipsoide
La altura h de elipsoide se expresa en metros en las fórmulas anteriores. Si la unidad z de su ráster de entrada se especifica en otra unidad, se transformará internamente a metros.
Cálculo de la orientación
La orientación geodésica en una ubicación es la dirección de la pendiente descendente respecto al norte, en un plano paralelo a la superficie del elipsoide.
Para calcular la orientación en cada ubicación, se ajusta un plano vecino con celdas de 3 x 3 alrededor de cada celda de procesamiento utilizando el método por mínimos cuadrados. El mejor ajuste en el método por mínimos cuadrados minimiza la suma de la diferencia cuadrada (dzi) entre el valor z real y el valor z ajustado. Consulte la ilustración a continuación para ver un ejemplo.
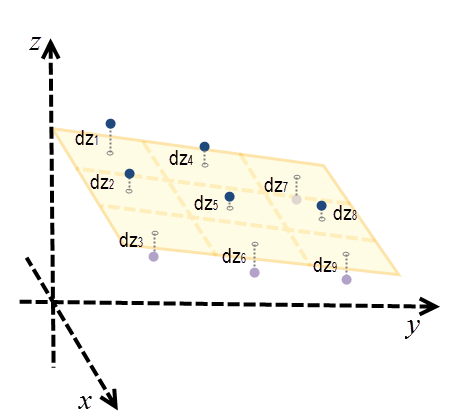
Aquí, el plano se representa como z = Ax + By + C. Para cada centro de celda, dzi es la diferencia entre el valor z real y el valor z ajustado.
El plano se ajusta mejor cuando ∑9i=1dzi2 se minimiza.
Una vez ajustado el plano, se calcula una superficie normal en la ubicación de la celda. En la misma ubicación, también se calcula un elipsoide normal perpendicular al plano tangente de la superficie de elipsoide.
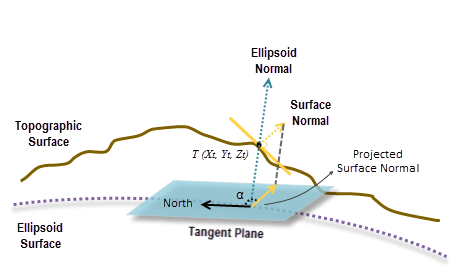
Dado que el plano tangente de la superficie elipsoide se considera el plano de referencia, la superficie normal se proyecta perpendicularmente en el plano. Finalmente, la orientación geodésica es calculada midiendo el ángulo α en el sentido de las agujas del reloj entre el norte y la proyección perpendicular de la superficie normal (consulte la ilustración de arriba).
Utilización de una GPU
Para el método geodésico, esta herramienta es capaz de aumentar el rendimiento si tiene determinado hardware de GPU instalado en su sistema. Consulte la sección Procesamiento de GPU con Spatial Analyst para obtener más información sobre la compatibilidad, cómo configurarla y cómo activarla.
Referencias
Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.
Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159
E.J.Krakiwsky, and D.E.Wells, 1971. Coordinate Systems In Geodesy (GEODESY AND GEOMATICS ENGINEERING, UNB), LECTURE NOTES, No16, 1971, pp. 18-38
Lancaster, P. and Šalkauskas, K. Curve and Surface Fitting: An Introduction. London: Academic Press, 1986.
B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice. Sección 10.2.1. p. 282.
David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.