Cómo funciona Relaciones bivariantes locales

Un componente importante de muchos flujos de trabajo de análisis de SIG es la comparación de dos variables en un área de estudio para determinar si dichas variables están relacionadas y el modo en que lo están. Por ejemplo: ¿existe una relación entre la diabetes y la obesidad en determinadas áreas? Históricamente, preguntas como esta se han respondido con comparaciones cartográficas minuciosas o análisis de regresión lineal. La comparación cartográfica puede ser subjetiva, y el análisis de regresión solo puede detectar relaciones simples.

La herramienta Relaciones bivariantes locales le permite cuantificar la relación entre dos variables en el mismo mapa al determinar si los valores de una variable dependen o se ven influidos por los valores de otra variable, y si dichas relaciones varían en el espacio geográfico. La herramienta calcula una estadística de entropía en cada vecindad local que cuantifica la cantidad de información compartida entre ambas variables. A diferencia de otras estadísticas que muchas veces solo pueden capturar relaciones lineales (por ejemplo, regresión lineal), la entropía puede capturar cualquier relación estructural existente entre las dos variables, incluidas relaciones exponenciales, cuadráticas, sinusoidales y hasta relaciones complejas que no se pueden representar mediante las típicas funciones matemáticas. Esta herramienta admite polígonos y puntos y crea una clase de entidad de salida que resume la importancia y la forma de las relaciones de cada entidad de entrada. Además, dispone de elementos emergentes personalizados y toda una variedad de diagnósticos, gráficos y mensajes.

Aplicaciones potenciales

La herramienta se puede utilizar en estos tipos de aplicaciones:

• El Centro de control y prevención de enfermedades (CDC, por sus siglas en inglés) afirma: "Las personas con obesidad, en comparación con las personas cuyo peso es normal o saludable, corren mayor riesgo de padecer numerosas enfermedades y problemas de salud graves, incluida la diabetes de tipo 2". El CDC podría utilizar esta herramienta para cuantificar la solidez de la relación entre obesidad y diabetes y determinar si dicha relación persiste en toda el área de estudio.
• Un funcionario de salud pública podría explorar las relaciones entre los niveles de contaminación del aire y los factores socioeconómicos con el fin de detectar posibles injusticias ambientales.

Método de la entropía

¿Qué significa que dos variables estén relacionadas entre sí? Existen muchos tipos de relaciones entre variables, pero, en el sentido más simple, dos variables están relacionadas si es posible obtener información acerca de una variable observando los valores de la otra variable. Por ejemplo, es posible obtener información sobre el riesgo de padecer diabetes observando información sobre la obesidad. Se conoce como dependencia entre dos variables y, por el contrario, si no es posible obtener información acerca de una variable observando la otra variable, las variables se consideran independientes.

Una forma de medir el grado de relación entre variables es a través de la entropía. La entropía es un concepto fundamental de la teoría de la información, utilizado para cuantificar la cantidad de incertidumbre en una variable aleatoria. Por lo general, cuanto menos predecible sea la variable, mayor será la entropía. La entropía tiene una aplicación muy amplia y se puede calcular para variables aleatorias individuales; también es posible calcular una entropía conjunta entre dos o más variables. La entropía conjunta de dos variables equivale a la entropía de la primera variable más la entropía de la segunda variable, menos la información mutua de ambas. La información mutua es una cuantificación útil del nivel de dependencia entre las variables, ya que mide directamente la cantidad de información que se puede obtener acerca de una variable observando los valores de la otra variable.

Para estimar la información mutua, se debe estimar tanto la entropía de cada variable individual como su entropía conjunta. Sin embargo, estos valores dependen de las distribuciones subyacentes de las variables y casi nunca se conocen en la práctica. Afortunadamente, estudios recientes han demostrado que es posible estimar la entropía conjunta de varias variables mediante árboles de expansión mínima de potencia ponderada como indicador de la distribución conjunta de las variables (Guo, 2010). De este modo, es posible estimar la entropía conjunta sin conocer las distribuciones individuales de las dos variables. Poder estimar la entropía conjunta resulta útil. Sin embargo, para poder determinar si las dos variables están relacionadas, lo que realmente necesita conocer es la información mutua entre las variables. Si bien no es posible estimar directamente la información mutua sin conocer las distribuciones de las dos variables, sí es posible utilizar permutaciones para construir una prueba de hipótesis nula para relaciones estadísticamente significativas.

Probar relaciones significativas mediante permutaciones

Como hemos visto en la sección anterior, la pregunta de si dos variables están relacionadas equivale a preguntar si su entropía conjunta (la cual es posible estimar) es significativamente menor que la suma de las entropías individuales de las dos variables (la cual no es posible estimar). Dicho de otro modo: ¿La entropía conjunta estimada de los datos es significativamente menor de lo que sería si ambas variables fueran independientes?

Para determinarlo, se realizan permutaciones en las variables, reasignando aleatoriamente cada valor de la primera variable a un nuevo valor de la segunda variable. Al aleatorizar las uniones, los datasets permutados no compartirán información mutua, pero las entropías individuales de las dos variables no cambiarán. Al generar muchos datasets permutados y estimar la entropía conjunta de cada uno de ellos, puede crear una distribución de la entropía conjunta en la hipótesis nula de que las dos variables son independientes y no están relacionadas. A continuación, podemos comparar la entropía conjunta estimada a partir de los datos reales con esta distribución, así como calcular un pseudo valor P según la proporción de las permutaciones cuya entropía conjunta sea menor que la entropía conjunta de los datos reales.

Probar relaciones espaciales locales

El procedimiento descrito anteriormente sobre probar relaciones significativas entre dos variables se puede aplicar a cualquier tipo de datos bivariantes continuos. Para convertirlo en una prueba de las relaciones espaciales locales, esta prueba de hipótesis se realiza en cada entidad de entrada utilizando vecindades. De este modo, puede representar los resultados en un mapa e identificar las áreas locales donde las variables mantienen una relación significativa.

La escala de todos los valores de los parámetros Variable dependiente y Variable explicativa se modifica para que sea entre 0 y 1 restando el valor mínimo de todo el dataset y dividiéndolo por el rango (el máximo menos el mínimo) de todo el dataset. A continuación, se llevan a cabo los siguientes pasos para cada entidad de entrada:

1. Buscar las entidades vecinas más cercanas. El parámetro Cantidad de vecinos especifica cuántos vecinos se utilizarán. La entidad de entrada se cuenta como vecina de sí misma.
2. Fusionar los valores de las dos variables con la escala modificada de los vecinos en un solo dataset.
3. Construir el árbol de expansión mínima y estimar la entropía conjunta.
4. Permutar aleatoriamente los valores de las dos variables y estimar la entropía conjunta de cada permutación. El parámetro Número de permutaciones especifica cuántas permutaciones se realizarán.
5. Calcular el pseudo valor P y determinar si las variables mantienen una relación estadísticamente significativa.

Puesto que este procedimiento realiza una prueba de hipótesis distinta para cada entidad de entrada, puede utilizar el parámetro Aplicar corrección False Discovery Rate (FDR) para controlar la proporción de resultados falsos positivos (errores de tipo 1).

Clasificar las relaciones locales

Identificar las áreas en las que dos variables mantienen una relación estadísticamente significativa es muy importante. Para poder dar uso a esta información, conviene identificar el tipo de relación entre las variables en función de cómo prediga la variable explicativa el valor de la variable dependiente.

Cada entidad de entrada se clasificará en uno de los siguientes tipos de relaciones:

• No significativa: la relación entre las variables no es significativa estadísticamente.
• Lineal positiva: la variable dependiente aumenta linealmente a medida que aumenta la variable explicativa.
• Lineal negativa: la variable dependiente disminuye linealmente a medida que aumenta la variable explicativa.
• Cóncava: la variable dependiente cambia en forma de curva cóncava a medida que aumenta la variable explicativa. Por lo general, las curvas cóncavas se curvan o arquean hacia abajo.
• Convexa: la variable dependiente cambia en forma de curva convexa a medida que aumenta la variable explicativa. Por lo general, las curvas convexas se curvan o arquean hacia arriba.
• Complejo sin definir: las variables mantienen una relación significativa, pero ninguna de las otras categorías describe de forma fiable el tipo de relación.

Las siguientes imágenes son ejemplos de una relación Cóncava:

Se muestran ejemplos típicos de relaciones cóncavas entre dos variables.

Las siguientes imágenes son ejemplos de una relación Convexa:

Se muestran ejemplos típicos de relaciones convexas entre dos variables.

Clasifique cada entidad significativa con estos pasos:

1. Estime un modelo de regresión lineal ordinario para predecir la variable dependiente en función de la variable explicativa y calcule el Criterio de información de Akaike corregido (AICc) para el modelo.
2. Estime un segundo modelo de regresión lineal para predecir la variable dependiente en función de la variable explicativa y el cuadrado de la variable explicativa (modelo de regresión cuadrática) y calcule el AICc.
3. Compare los valores de AICc de los dos modelos de regresión y elija el que mejor represente la relación. El AICc del modelo de regresión cuadrático debe ser al menos 3 veces menor que el AICc del modelo de regresión lineal para poder elegir el modelo cuadrático. De lo contrario, deberá elegir el modelo lineal.
4. Calcule el valor R² ajustado para el modelo elegido. Si es menor que 0,05, el modelo elegido explica menos del 5 por ciento de la variación de los datos y la relación se clasifica como Complejo sin definir.
5. Si el R² ajustado es mayor que 0,05, realice la clasificación siguiendo estas reglas:
   • Si elige un modelo lineal y el coeficiente es positivo, se clasifica como Lineal positiva.
   • Si elige el modelo lineal y el coeficiente es negativo, se clasifica como Lineal negativa.
   • Si elige el modelo cuadrático y el coeficiente del término al cuadrado es positivo, se clasifica como Convexa.
   • Si elige el modelo cuadrático y el coeficiente del término al cuadrado es negativo, se clasifica como Cóncava.

Interpretar los resultados

La salida de esta herramienta es una clase de entidad simbolizada por el tipo de relación, junto con estadísticas de resumen que aparecen en mensajes de geoprocesamiento. Las entidades de salida contienen campos informativos y elementos emergentes que visualizan la relación con gráficos de dispersión.

Gráficos de dispersión emergentes

Si se especifica, se generan gráficos de dispersión emergentes personalizados para cada entidad de salida, que se pueden visualizar al hacer clic en la entidad del mapa. La siguiente imagen muestra un gráfico de dispersión emergente para una entidad con una relación lineal positiva:

Se muestra un gráfico de dispersión emergente para una relación lineal positiva.

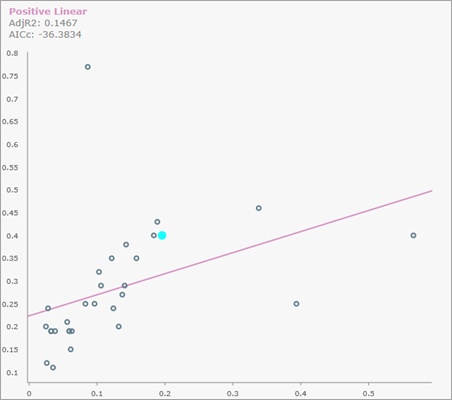
La variable explicativa con la escala modificada se muestra en el eje x; la variable dependiente con la escala modificada, en el eje y. El único punto resaltado en el gráfico de dispersión es la entidad; el resto de puntos son vecinos de la entidad.

Desplácese sobre un punto del gráfico de dispersión para ver el Id. de origen de la entidad y los valores con la escala modificada de las variables dependientes y explicativas, junto con sus valores sin procesar (la escala original) entre paréntesis.

Mensajes de geoprocesamiento

La información de resumen sobre la importancia estadística y los tipos de relaciones aparecen como mensajes de geoprocesamiento. A continuación, se muestra un ejemplo de dichos mensajes.

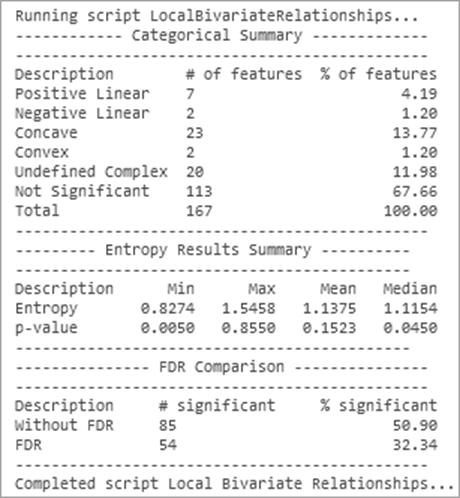
La sección Resumen de categorías del mensaje enumera el número de entidades y los porcentajes de cada tipo de relación. La sección Resumen de resultados de entropía enumera el mínimo (Mín.), máximo (Máx.), promedio (Valor medio) y mediana (Mediana) de la entropía y los valores P de las entidades de entrada. La sección Comparación FDR enumera el número y porcentaje de las relaciones estadísticamente significativas aplicando y sin aplicar una corrección de índice de descubrimientos falsos.

Nota:

Los mensajes de geoprocesamiento aparecen en la parte inferior del panel Geoprocesamiento durante la ejecución de la herramienta. También puede acceder a los mensajes con el historial de geoprocesamiento desplazándose sobre la barra de progreso y haciendo clic en el botón emergente o expandiendo la sección de mensajes del panel Geoprocesamiento.

Campos de salida

La salida de la herramienta contiene varios campos que proporcionan información sobre cómo y por qué cada entidad se clasificó en su tipo de relación.

Importancia de relación

Los siguientes campos ofrecen información sobre si la relación entre las variables dependientes y explicativas es estadísticamente significativa:

• Entropy: el valor de entropía estimado para la entidad.
• P-values: el seudovalor P de la prueba para una relación significativa entre las variables dependiente y explicativa. Este valor no se ajusta para el índice de descubrimientos falsos.
• Local Bivariate Relationship Confidence Level: el mayor nivel de confianza que se cumple para la entidad. Los posibles valores de este campo son 90 % de confianza, 95 % de confianza, 99 % de confianza y No significativo. El nivel de confianza se ajusta para el índice de descubrimientos falsos si se especifica un valor para el parámetro Aplicar corrección False Discovery Rate (FDR).

Clasificación de relación

Los siguientes campos ofrecen información sobre la clasificación del tipo de relación entre las variables dependiente y explicativa:

• Type of Relationship: el tipo de relación entre las variables dependiente y explicativa
• AICc (Linear): el criterio de información de Akaike corregido para el modelo lineal
• R-squared (Linear): el valor R² del modelo lineal
• AICc (Polynomial): el criterio de información de Akaike corregido para el modelo polinómico
• R-squared (Polynomial): el valor R² del modelo polinómico

Nota:

Los valores AICc y R² serán nulos para las entidades que no tengan una relación estadísticamente significativa entre las variables dependiente y explicativa.

Coeficientes de regresión e importancia

Los siguientes campos ofrecen información sobre los coeficientes de los modelos lineal y polinómico que se utilizan para clasificar la relación:

• Intercept: interceptación del modelo lineal.
• Coefficient (Linear): coeficiente del término lineal del modelo lineal.
• Polynomial Intercept: interceptación del modelo polinómico.
• Polynomial Coefficient (Linear): coeficiente del término lineal del modelo polinómico.
• Polynomial Intercept (Squared): coeficiente del término al cuadrado del modelo polinómico.
• Significance of Coefficients (Linear): código de dos caracteres que indica si la interceptación y el coeficiente son estadísticamente significativos en un nivel de confianza del 90 por ciento. Un guion bajo (_) indica que el valor no es estadísticamente significativo y un asterisco (*) indica que el valor sí es estadísticamente significativo. Por ejemplo, *_ indica que la interceptación es estadísticamente significativa, pero el coeficiente lineal no lo es. Del mismo modo, *_ indica que la interceptación no es estadísticamente significativa, pero el coeficiente lineal sí lo es.
• Significance of Coefficients (Polynomial): código de tres caracteres que indica si la interceptación, el coeficiente lineal y el coeficiente al cuadrado del modelo polinómico son estadísticamente significativos en un nivel de confianza del 90 por ciento. Por ejemplo, *_* indica que la interceptación es estadísticamente significativa, el coeficiente lineal no lo es y el coeficiente al cuadrado sí.

Nota:

Todos los campos relacionados con coeficientes de regresión serán cadenas de caracteres vacías o nulas para cada entidad que no tenga una relación estadísticamente significativa entre las variables dependiente y explicativa.

Sugerencias

Tenga en cuenta estas sugerencias al utilizar la herramienta Relaciones bivariantes locales:

• Utilice el parámetro Factor de escala para controlar la sensibilidad de la herramienta ante relaciones sutiles. Los factores de escala cercanos a cero solamente detectarán relaciones sólidas entre las variables; los factores de escala cercanos a uno pueden detectar además relaciones más débiles. El valor predeterminado de 0,5 supone un equilibrio: se detectarán relaciones sólidas y moderadas.
• El valor del parámetro Cantidad de vecinos que elija tiene varias implicaciones importantes. Usar una mayor cantidad de vecinos ofrece más datos para cada prueba de hipótesis, lo que aumenta la probabilidad de detectar una relación significativa. Sin embargo, si se usan muchos vecinos, la prueba será menos local, porque debe buscar más lejos para encontrar vecinos, por lo que no se detectarían relaciones muy locales. Las grandes cantidades de vecinos también aumentan rápidamente el tiempo de ejecución de la herramienta.
• El valor del parámetro Número de permutaciones que elija supone un equilibrio entre la precisión y un mayor tiempo de procesamiento. Al aumentar el número de permutaciones se incrementa la precisión porque aumenta el rango de posibles valores para el pseudo P. Por ejemplo, con 99 permutaciones, la precisión del pseudo valor P es de 0,01 y para 999 permutaciones, la precisión es de 0,001. Estos valores se calculan al dividir 1 entre la cantidad de permutaciones más 1: 1/(1+99) y 1/(1+999). Se puede utilizar un número inferior de permutaciones al explorar un problema por primera vez, pero la práctica recomendada es aumentar las permutaciones al número más alto viable de cara a los resultados finales. También se recomienda utilizar un mayor número de permutaciones si se usa un número mayor de vecinos.

Cita

• Guo, D. "Local entropy map: a nonparametric approach to detecting spatially varying multivariate relationships". International Journal of Geographical Information Science 24, n.º 9 (septiembre de 2010): 1367-1389.