Disponible con una licencia de Spatial Analyst.
Disponible con una licencia de 3D Analyst.
La herramienta Sombreado obtiene la iluminación hipotética de una superficie determinando los valores de iluminación para cada celda de un ráster. Para esto, se configura la posición de una fuente de luz hipotética y se calculan los valores de iluminación de cada celda respecto de las celdas vecinas. Esto puede mejorar mucho la visualización de una superficie para su análisis o visualización gráfica, en especial cuando se utiliza la transparencia.
Por defecto, la sombra y la luz son tonos de grises asociados a números enteros, de 0 a 255 (aumenta de negro a blanco).
Parámetros de sombreado
El factor principal al crear un mapa de sombreado para cualquier ubicación es la ubicación del sol en el cielo.
Acimut
El acimut es la dirección angular del sol, medida de 0 a 360 grados desde el Norte en el sentido de las agujas del reloj. Un acimut de 90 grados es Este. El acimut predeterminado es 315 grados (NO).

Altitud
La altitud es la pendiente o el ángulo de la fuente de iluminación por encima del horizonte. Las unidades se expresan en grados, de 0 (en el horizonte) a 90 (arriba). El valor predeterminado es 45 grados.
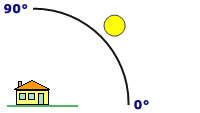
Ejemplo de sombreado
En el siguiente ejemplo de sombreado, el acimut es de 315 grados y la altitud es de 45 grados.

Usar el sombreado para la visualización
Colocando un ráster de elevación sobre un ráster de sombreado y ajustando la transparencia utilizando el control deslizante Transparencia de capa sobre la pestaña Apariencia del ráster de elevación, puede crear fácilmente un mapa de relieve visualmente atractivo de un paisaje.

Puede agregar otras capas, como tipos de uso del suelo, vegetación, carreteras o arroyos para aumentar aún más el contenido de información en la visualización.
Usar el sombreado para el análisis
Al modelar el tono (la opción predeterminada), puede calcular la iluminación local y si la celda cae en una sombra o no.
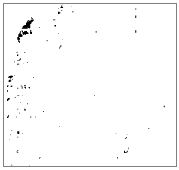
Al modelar la sombra, puede identificar la celdas que estarán a la sombra de otra celda en un momento particular del día. Las celdas que se encuentran en la sombra de otra celda se codifican con 0; todas las otras celdas se codifican con números enteros desde 1 a 255. Puede clasificar todos los valores mayores que 1 a 1, produciendo un ráster de salida binario. En el ejemplo siguiente, las áreas negras están a la sombra. El acimut es el mismo en cada imagen, pero se modifica el ángulo (la altitud) del sol.

Cómo se calcula el sombreado
Para calcular el valor del tono, primero se necesita la altitud y el acimut de la fuente de iluminación. Estos valores se procesan con los cálculos de pendiente y orientación para determinar el valor final de sombreado de cada celda del ráster de salida.
Algoritmo de sombreado
El algoritmo para calcular el valor de sombreado es el siguiente:
(1) Sombreado = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) +
(sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad)))Tenga en cuenta que si el cálculo del valor de sombreado es < 0, el valor de la celda de salida será = 0.
Calcular el ángulo de iluminación
La altitud de la fuente de iluminación se especifica en grados por encima de la horizontal. Sin embargo, la fórmula para calcular el valor de sombreado requiere que el ángulo esté representado en radianes y que sea la desviación de la vertical. La dirección recta hacia arriba desde la superficie (directamente arriba) se denomina Cénit. El ángulo cénit se mide desde el punto del cénit hacia la dirección de la fuente de iluminación y es el complemento de 90 grados de la altitud. Para calcular el ángulo de iluminación, primero debe convertir el ángulo de altitud en ángulo cénit. Después convierta el ángulo a radianes.
Cambar la altitud a ángulo cénit:
(2) Zenith_deg = 90 - AltitudConvertir a radianes:
(3) Zenith_rad = Zenith_deg * pi / 180.0Calcular la dirección de iluminación
La dirección de la fuente de iluminación, el acimut, se especifica en grados. La fórmula de sombreado requiere que este ángulo se exprese en unidades de radianes. Primero, se cambia el ángulo acimutal de su unidad geográfica (dirección de brújula) a una unidad matemática (ángulo recto). A continuación, el ángulo acimutal se convierte a radianes.
Cambiar la medida del ángulo acimutal:
(4) Azimuth_math = 360.0 - Acimut + 90Tenga en cuenta que si Azimuth_math >= 360,0, entonces:
(5) Azimuth_math = Azimuth_math - 360.0Convertir a radianes:
(6) Azimuth_rad = Azimuth_math * pi / 180.0Calcular la pendiente y la orientación
Una ventana de 3 x 3 móvil visita cada celda del ráster de entrada y, para cada celda en el centro de la ventana, se calcula un valor de orientación y de pendiente mediante un algoritmo que incorpora los valores de las ocho vecinas de la celda. Las celdas se identifican como letras, de la a a la i, con la letra e representando la celda para la cual se calcula la orientación.
La tasa de cambio en la dirección x de la celda e se calcula con el siguiente algoritmo:
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize)La tasa de cambio en la dirección y de la celda "e" se calcula con el siguiente algoritmo:
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize)La pendiente es el descenso cuesta abajo más empinado desde cada celda en la superficie. El algoritmo para calcular la pendiente en radianes, incorporando el factor z es:
(9) Slope_rad = ATAN (z_factor * √ ([dz/dx]2 + [dz/dy]2)) La orientación es la dirección hacia donde apunta la pendiente descendente más empinada. La orientación en radianes se define en el rango de 0 a 2pi, con el 0 hacia el este. La orientación se determina según las reglas del siguiente algoritmo:
(10) If [dz/dx] is non-zero:
Aspect_rad = atan2 ([dz/dy], -[dz/dx]) if Aspect_rad < 0 then Aspect_rad = 2 * pi + Aspect_rad If [dz/dx] is zero:
if [dz/dy] > 0 then Aspect_rad = pi / 2 else if [dz/dy] < 0 then Aspect_rad = 2 * pi - pi / 2 else Aspect_rad = Aspect_radEjemplo de cálculo de sombreado
En este ejemplo, se calcula el valor del sombreado de la celda central de la ventana móvil.
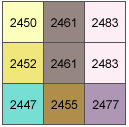
El tamaño de la celda es de 5 unidades. Se van a utilizar la Altitud predeterminada de 45 grados y un Acimut de 315 grados.
- Ángulo de iluminación
El cálculo del Ángulo cénit con la ecuación 2 es:
(2) Zenith_deg = 90 - Altitud = 90 - 45 = 45Y convertido a radianes con la ecuación 3 es:
(3) Zenith_rad = Zenith_deg * pi / 180.0 = 45 * 3.1428571429 / 180 = 0.7857142857 - Dirección de iluminación
El cálculo para convertir el ángulo acimutal de geográfico a matemático con la ecuación 4 es:
(4) Azimuth_math = 360.0 - Acimut + 90 = 360.0 - 315 + 90 = 135 = 2.3571428571La conversión del ángulo acimutal a radianes con la ecuación 6 es:
(6) Azimuth_rad = Azimuth_math * pi / 180.0 = 135 * 3.1438571429 / 180
- Pendiente y orientación
El cálculo de la tasa de cambio en la dirección x de la celda central e es:
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize) = ((2483 + 4966 + 2477) - (2450 + 4904 + 2447)) / (8 * 5) = (9926 - 9801)/ 40 = 3.125El cálculo de la tasa de cambio en la dirección y de la celda central e es:
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize) = (2447 + 4910 + 2477) - (2450 + 4922 + 2483) / (8 * 5) = (9834 - 9855) / 40 = -0.525El cálculo del ángulo de la Pendiente es:
(9) Slope_rad = ATAN ( z_factor * √ ([dz/dx]2 + [dz/dy]2)) = atan(1 * sqrt(3.125 * 3.125 + -0.525 * -0.525)) = 1.26511El cálculo para el ángulo Aspect_rad desde la norma 10 es (dado que dz/dx es distinto de cero en este ejemplo):
Aspect_rad = atan2 ([dz/dy], -[dz/dx]) = atan2(-0.525, -3.125) = -2.9751469600412Como el valor es menor que 0, se aplica esta parte de la regla:
Aspect_rad = 2 * pi + Aspect_rad = 2 * 3.1428571429 + -2.9751469600412 = 3.310567 - Sombreado
El cálculo final del sombreado es:
HSombreado = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad))) = 255.0 * ((cos(0.7857142857) * cos(1.26511)) + (sin(0.7857142857) * sin(1.26511) * cos(2.3571428571 - 3.310567))) = 153.82
Dado que el ráster de salida es del tipo número entero, el valor de sombra para la celda central e = 154.
Referencias
Burrough, P. A. y McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.