Disponible con una licencia de Geostatistical Analyst.
The semivariogram and covariance functions are theoretical quantities that you cannot observe, so you estimate them from your data using what are called the empirical semivariogram and empirical covariance functions. Often, you can gain insight into the quantities by looking at the way they are estimated. Suppose you take all pairs of data that are a similar distance and direction from each other.
For all the pairs of locations si and sj that are a similar distance and direction from each other, compute
average[(z(si) - z(sj))2]where z(si) is the measured value at location si.
If all the pairs of locations si and sj are close to each other, it's expected that z(si) and z(sj) will be similar in value, so when you take the differences and square them, the average should be small. As si and sj get farther apart, it's expected that their values will become more dissimilar, so when you take their differences and square them, the average will get larger.
In the covariance function, for all the pairs of locations si and sj that are a similar distance and direction from each other, the software computes
average [(Z(si)-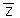 )(Z(s j)-
)(Z(s j)-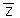 )],
)],
where z(si) is the measured value at location si and
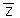 is the mean of all of the data. Now, if all the pairs si and sj are close to each other, it's expected either that both z(si) and z(sj)
will be above the mean
is the mean of all of the data. Now, if all the pairs si and sj are close to each other, it's expected either that both z(si) and z(sj)
will be above the mean 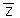 or both will be below the mean. Either way, their product is positive, so when you average all of the products, you expect a positive value. If si and sj are far apart, it's expected that about half the time the products will be negative and half the time they will be positive, so you expect their average to be near zero.
or both will be below the mean. Either way, their product is positive, so when you average all of the products, you expect a positive value. If si and sj are far apart, it's expected that about half the time the products will be negative and half the time they will be positive, so you expect their average to be near zero.