Disponible con una licencia de Geostatistical Analyst.
The semivariogram and covariance functions quantify the assumption that things nearby tend to be more similar than things that are farther apart. Semivariogram and covariance both measure the strength of statistical correlation as a function of distance.
The process of modeling semivariograms and covariance functions fits a semivariogram or covariance curve to your empirical data. The goal is to achieve the best fit, and also incorporate your knowledge of the phenomenon in the model. The model will then be used in your predictions.
When fitting a model, explore for directional autocorrelation in your data. The sill, range, and nugget are the important characteristics of the model. If there are measurement errors in the data, use a measurement error model. Follow this link to learn how to fit a model to the empirical semivariogram.
Semivariogram
The semivariogram is defined as
γ(si,sj) = ½ var(Z(si) - Z(sj)),where var is the variance.
If two locations, si and sj, are close to each other in terms of the distance measure of d(si, sj), you expect them to be similar, so the difference in their values, Z(si) - Z(sj), will be small. As si and sj get farther apart, they become less similar, so the difference in their values, Z(si) - Z(sj), will become larger. This can be seen in the following figure, which shows the anatomy of a typical semivariogram.
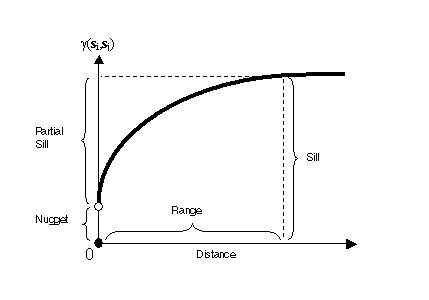
Notice that the variance of the difference increases with distance, so the semivariogram can be thought of as a dissimilarity function. There are several terms that are often associated with this function, and they are also used in Geostatistical Analyst. The height that the semivariogram reaches when it levels off is called the sill. It is often composed of two parts: a discontinuity at the origin, called the nugget effect, and the partial sill; added together, these give the sill. The nugget effect can be further divided into measurement error and microscale variation. The nugget effect is simply the sum of measurement error and microscale variation and, since either component can be zero, the nugget effect can be composed wholly of one or the other. The distance at which the semivariogram levels off to the sill is called the range.
Covariance function
The covariance function is defined to be
C(si, sj) = cov(Z(si), Z(sj)),where cov is the covariance.
Covariance is a scaled version of correlation. So, when two locations, si and sj, are close to each other, you expect them to be similar, and their covariance (a correlation) will be large. As si and sj get farther apart, they become less similar, and their covariance becomes zero. This can be seen in the following figure, which shows the anatomy of a typical covariance function.
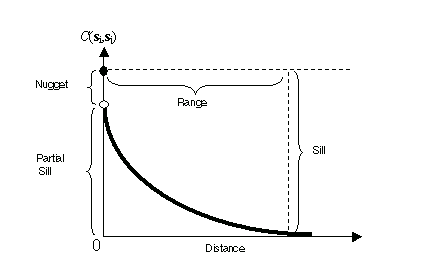
Notice that the covariance function decreases with distance, so it can be thought of as a similarity function.
Relationship between semivariogram and covariance function
There is a relationship between the semivariogram and the covariance function:
γ(si, sj) = sill - C(si, sj),This relationship can be seen from the figures. Because of this equivalence, you can perform prediction in Geostatistical Analyst using either function. (All semivariograms in Geostatistical Analyst have sills.)
Semivariograms and covariances cannot be just any function. For the predictions to have nonnegative kriging standard errors, only some functions may be used as semivariograms and covariances. Geostatistical Analyst offers several choices that are acceptable, and you can try different ones for your data. You can also have models that are made by adding several models together—this construction provides valid models, and you can add up to four of them in Geostatistical Analyst. There are some instances when semivariograms exist, but covariance functions do not. For example, there is a linear semivariogram, but it does not have a sill, and there is no corresponding covariance function. Only models with sills are used in Geostatistical Analyst. There are no hard-and-fast rules on choosing the "best" semivariogram model. You can look at your empirical semivariogram or covariance function and choose a model that looks appropriate. You can also use validation and cross-validation as a guide.