Disponible con una licencia de Spatial Analyst.
La herramienta Coste-conectividad tiene por finalidad definir la red óptima de rutas de menor coste y no la creación de rutas separadas que conectan regiones. En la red resultante, el fenómeno puede moverse de una región a otra utilizando las rutas (posiblemente viajando a través de otras regiones).
Ejemplos de problemas solucionados con la herramienta Coste-conectividad
- A partir de un modelo de adecuación, ha identificado 10 de los mejores terrenos de hábitat para los linces. Quiere que los linces se muevan entre los terrenos utilizando la red más efectiva de corredores de vida salvaje para mantener la diversidad genética dentro de la metapoblación.
- En un despliegue militar para una misión de paz, ha identificado 5 áreas en las que se deben situar las tropas y el personal. Quiere desarrollar la mejor red de rutas de suministro entre las bases.
- En una explotación maderera, desea crear la red más rentable de caminos de tala forestal para extraer la madera.
Cómo funciona el algoritmo de Coste-conectividad
En los pasos siguientes se indica, conceptualmente, cómo funciona el algoritmo Coste-conectividad:
- Se identifican las fuentes de entrada y la superficie de coste.
En el gráfico de abajo, las regiones de entrada (los polígonos coloreados) se muestran sobre la capa de superficie de coste.
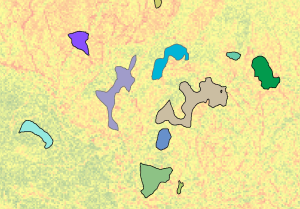
Las regiones de entrada se muestran sobre el ráster de superficie de coste. - Se realiza una Asignación de costes.
En el gráfico de abajo, las regiones de entrada se muestran sobre la capa de asignación de costes asociada. El valor de cada celda en el ráster de asignación corresponde a la región concreta a la que se puede llegar con el coste acumulado más barato (más bajo).
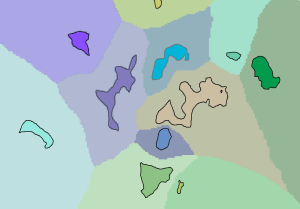
Regiones mostradas sobre la capa de asignación de costes - Se crean rutas de coste entre cada región y su región de costes vecina.
En el gráfico de abajo, las regiones de entrada y las rutas de menor coste de cada región respecto a su región de costes vecina (líneas magenta) se muestran sobre la capa de asignación de costes asociada.
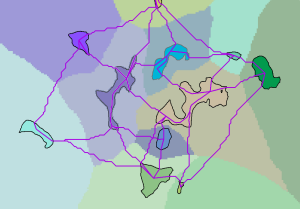
Asignación de costes con regiones conectadas mediante rutas - Las regiones y las rutas resultantes se convierten en un gráfico (en la teoría de grafos). En la conversión, las regiones son los vértices y las rutas son los bordes. El coste acumulado de la ruta corresponde al peso del borde.
Desde el punto de vista conceptual, la conversión de las regiones y las rutas en la teoría de grafos se pueden representar mediante la ilustración siguiente. Los círculos numerados son los vértices (las regiones) y las líneas de conexión entre los vértices son los bordes (las rutas de menor coste). Los pesos de los bordes son el coste acumulado de las rutas. En la ilustración, cuanto mayor es el coste, más gruesa es la línea.
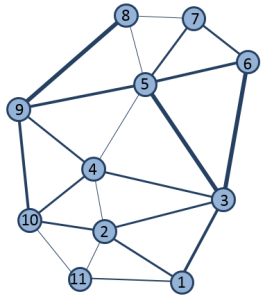
Ilustración conceptual de la teoría de grafos Nota:
Para comprender bien cómo funciona esta herramienta, es recomendable tener unos conocimientos básicos de la teoría de grafos. Existen muchos recursos que puede consultar, pero puede empezar por esta entrada de la Wikipedia: https://en.wikipedia.org/wiki/Graph_theory.
- El árbol de expansión mínima se determina utilizando la teoría de grafos para conectar los vértices (las regiones) de la forma más eficaz posible (menor coste).
Nota:
Hay más información sobre los árboles de expansión mínima on-line, como esta entrada de Wikipedia: https://en.wikipedia.org/wiki/Minimum_spanning_tree.
- La representación espacial de las regiones y las rutas del árbol de expansión mínima se asigna de nuevo en una clase de entidad de salida.
En el gráfico de abajo, las regiones de entrada y la red de rutas de menor coste del árbol de expansión mínima (color magenta) se muestran sobre la capa de superficie de coste asociada.
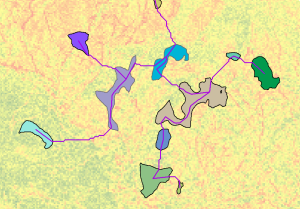
Rutas de salida entre regiones mostradas sobre el ráster de costes - También es posible que una clase de entidad de las rutas respecto a las regiones de coste vecinas constituya la salida (consulte el paso 3 arriba).
Cada ruta será una entidad lineal separada y habrá líneas duplicadas donde los corredores recorren un segmento común.
Si las regiones de entrada son polígonos, las rutas continúan hacia un punto dentro del polígono para permitir que el viajero entre por una ruta, se mueva dentro de la región y salga por otra ruta para llegar a otra región lejana. No se asigna ningún coste a estos segmentos ampliados dentro de una región; por lo tanto, no supone ningún coste moverse dentro de la región. Lo mismo ocurre en el caso de las regiones lineales: no supone ningún coste moverse a lo largo de la entidad lineal para llegar a otra ruta.
En el gráfico de abajo, el lado izquierdo es el resultado de utilizar la secuencia de las herramientas Coste de distancia y Ruta de coste para conectar regiones. Observe que las rutas solo llegan al borde de las regiones. En la imagen de la derecha se muestra la red resultante de rutas que conectan las regiones mediante la herramienta Coste-conectividad. Observe que las rutas continúan dentro de la región, lo que permite que el viajero acceda a la región por una ruta y salga por otra.
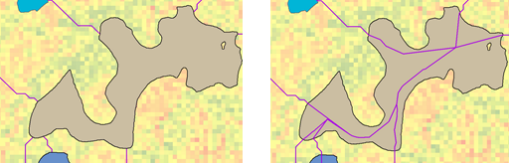
La importancia de las regiones
La entrada para la herramienta Coste-conectividad deben ser regiones. Una región es una serie de celdas conectadas (adyacentes) con el mismo valor. Si tiene celdas desconectadas con el mismo valor, estas serán zonas. Las zonas se pueden convertir en regiones utilizando la herramienta Grupo de regiones. La herramienta Coste-conectividad conecta cada región con las demás, de modo que, se puede llegar a todas las regiones y celdas dentro de las regiones mediante la red resultante.
Los escenarios del flujo de trabajo de Coste-conectividad
A continuación se indican escenarios comunes para utilizar la herramienta Coste-conectividad.
- La red óptima (el árbol de expansión mínimo) es la salida que se desea.
- Agregue rutas específicas a la red óptima utilizando las herramientas Coste de distancia y Ruta de coste para conectar las regiones por motivos que la red óptima no captura. Por ejemplo, agregando un sendero de evacuación para que los bomberos puedan huir de un incendio descontrolado.
- Cree la red que desee a partir de la salida opcional de todas las rutas hacia regiones vecinas utilizando su conocimiento especializado para eliminar rutas innecesarias.
- Convierta cualquiera de los escenarios anteriores en una red de Network Analyst y lleve a cabo análisis adicionales del movimiento entre las regiones.