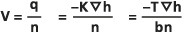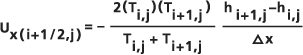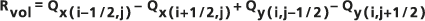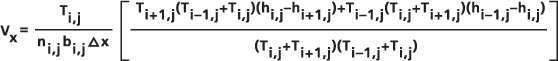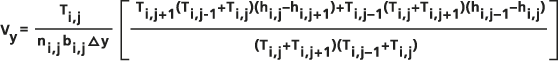Disponible con una licencia de Spatial Analyst.
El Flujo Darcy y la Velocidad Darcy, junto con el Recorrido de una partícula y la Dispersión tipo puff, se pueden utilizar para realizar modelos rudimentarios de advección-dispersión de los constituyentes de las aguas subterráneas. Esta metodología modela flujo bidimensional, verticalmente mezclado, horizontal y en estado estacionario, donde la altura es independiente de la profundidad.
Cálculos de flujo darcianos
Las ecuaciones utilizadas en el cálculo del flujo darciano se detallan en las siguientes secciones.
Calcular el flujo y la velocidad
La Ley de Darcy establece que la velocidad Darcy q en un medio poroso se calcula a partir de la conductividad hidráulica K y el gradiente de altura
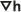(el cambio de altura por unidad de longitud en la dirección del flujo en un acuífero isotrópico) como:- q = -K
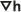
donde K puede calcularse a partir de la capacidad de transmisión T y el grosor b como K = T/b.
Este q, con unidades de volumen/tiempo/área, también se conoce como la descarga específica, el flujo volumétrico o la velocidad de filtración. Bear (1979) lo define como el volumen de agua que fluye por unidad de tiempo a través de una unidad de área de sección transversal normal a la dirección del flujo.
- q = -K
Estrechamente relacionado con este flujo volumétrico está el flujo del acuífero U, que es la descarga por unidad de ancho del acuífero (con unidades de volumen/tiempo/longitud):
- U = -T
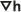
Esta construcción asume que la altura es independiente de la profundidad, de modo que el flujo es horizontal.
- U = -T
La velocidad promedio del fluido dentro de los poros, llamada velocidad de filtrado V, es la velocidad Darcy dividida por la porosidad efectiva del medio:
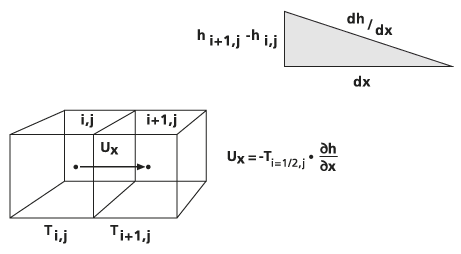
En la implementación del Flujo Darcy, es esta velocidad de filtrado V la que se calcula celda por celda. Para las celdas i,j, el flujo del acuífero U se calcula a través de cada una de las cuatro paredes de las celdas, utilizando la diferencia de altura entre las dos celdas adyacentes y el promedio armónico de las capacidades de transmisión Ti+1/2,j (Konikow y Bredehoeft, 1978 ), que se supone que son isotrópicas.
Por ejemplo, para el compontente x del
, la ecuación entre las celdas i,j y i+1,j sería:- δh/δx ≈ (hi+1 - hi) / Δx
Este esquema se muestra en los gráficos siguientes:
Calculando volumen residual
En el cálculo de la pared de celda siguiente, el flujo del acuífero entre la celda i,j y la celda i+1,j fluye paralelo a la dirección x y se calcula como:
Para determinar un balance de volumen de agua subterránea, se debe calcular la descarga de agua subterránea a través de la pared de la celda. Esta descarga Q x(i+1/2) se calcula a partir del flujo del acuífero U y el ancho de la pared de la celda Δy como:
- Qx(i+1/2,j) = Ux(i+1/2,j) Δy
Se obtienen valores similares para las cuatro paredes de la celda. Estos valores se utilizan para calcular el balance del volumen de agua subterránea residual Rvol para la celda, que se escribe en el ráster de salida. Este valor representa el excedente (o, en el caso de un número negativo, el déficit) de agua en cada celda dado el flujo neto hacia la celda, calculado como:
Este Rvol residual idealmente debería ser cero para todas las celdas. Al examinar el ráster de salida que contiene los valores residuales, busque desviaciones de cero. Grandes residuales, positivos o negativos, indican una producción o pérdida de masa, lo que viola el principio de continuidad y sugiere datos inconsistentes de carga y capacidad de transmisión. Patrones consistentes de residuales positivos o negativos sugieren que hay fuentes o sumideros no identificados. Reduzca los residuales antes de realizar cualquier otro modelado. Normalmente, se realizan ajustes en el campo de la capacidad de transmisión para reducir los residuales.
Calculando vectores de flujo
Las ecuaciones reales utilizadas en el Flujo Darcy para calcular los vectores de flujo para cada celda se condensan a partir del promedio aritmético de Ux (i-1/2,j) y Ux (i + 1/2, j), dividido por la porosidad de la celda central ni,j y el grosor bi,j para dar un valor para la velocidad de filtrado Vx en el centro:
y se usa una ecuación similar para calcular V y en el centro:
Este centrado se realiza para ajustarse a la convención de que los valores almacenados representan valores en el centro de la celda. Estos valores se convierten en dirección y magnitud en coordenadas geográficas para su almacenamiento en los rásteres de dirección y magnitud de salida.
En el caso de las celdas delimitadoras del ráster en las que la información está incompleta, los valores de velocidad simplemente se copian de la celda interior más cercana.
Valores de porosidad
Las tablas siguientes resumen algunos valores de porosidad y conductividad hidráulica para una variedad de medios geológicos.
Tabla 1: Conductividades hidráulicas de medios no consolidados
| Medio | K (m/s) |
|---|---|
Grava gruesa | 10-1 - 10-2 |
Arena y grava | 10-1 - 10-5 |
Arena fina, limo, loess | 10-5 - 10-9 |
Arcilla, lutita, sedimento glacial | 10-9 - 10-13 |
Tabla 2: Conductividades hidráulicas de medios consolidados
| Medio | K (m/s) |
|---|---|
Caliza dolomítica |
10-3 - 10-5 |
Tiza erosionada |
10-3 - 10-5 |
Tiza no erosionada |
10-6 - 10-9 |
Caliza |
10-5 - 10-9 |
Arenisca |
10-4 - 10-10 |
Granito, gneis, basalto compacto |
10-9 - 10-13 |
Tabla 3: Porosidades de los medios geológicos
| Medio | Porosidad total |
|---|---|
Granito y gneis inalterados | 0,0002 - 0,018 |
Cuarcita | 0,008 |
Lutita, pizarra, esquisto de mica | 0,005 - 0,075 |
Caliza, dolomita primaria | 0,005 - 0,125 |
Dolomita secundaria | 0,10 - 0,30 |
Tiza | 0,08 - 0,37 |
Arenisca | 0,035 - 0,38 |
Toba volcánica | 0,30 - 0,40 |
Arena | 0,15 - 0,48 |
Arcilla | 0,44 - 0,53 |
Arcilla expandida, limo | hasta 0,90 |
Suelo cultivable labrado | 0,45 - 0,65 |
Se proporcionan valores tabulados adicionales para la porosidad y la conductividad hidráulica en Freeze y Cherry (1979). Gelhar et al. (1992) presentan un resumen de la porosidad y capacidad de transmisión de varias formaciones específicas reportadas en la literatura. En Blatt et al. (1980) aparece una discusión detallada sobre la porosidad en materiales sedimentarios. En Tauxe (1994) se presenta un análisis completo del modelado de advección-dispersión utilizando estas funciones.
Ejemplos
La secuencia típica para modelar la dispersión de aguas subterráneas es realizar Flujo Darcy, después Recorrido de una partícula y, luego, Dispersión tipo puff.
- A continuación, se muestra un ejemplo de la configuración que se debe realizar en el cuadro de diálogo de la herramienta para el Flujo Darcy:
Ráster de altura de agua subterránea de entrada: altura
Ráster de porosidad de formación efectiva de entrada: poros
Ráster de grosor saturado de entrada: thickn
Ráster de capacidad de transmisión de la formación de entrada: transm
Ráster del balance del volumen de agua subterránea de salida: resid1
Ráster de dirección de salida : dir1
Ráster de magnitud de salida : mag1
- A continuación, se muestra un ejemplo de la configuración que se debe realizar en el cuadro de diálogo de la herramienta para la Velocidad Darcy:
Ráster de altura de agua subterránea de entrada: altura
Ráster de porosidad de formación efectiva de entrada: poros
Ráster de grosor saturado de entrada: thickn
Ráster de capacidad de transmisión de la formación de entrada: transm
Ráster de dirección de salida : dir1
Ráster de magnitud de salida : mag1
Referencias
Bear, J. Hydraulics of Groundwater. McGraw-Hill. 1979
Blatt, H., G. Middleton, and R. Murray. Origin of Sedimentary Rocks, 2ª Ed. Prentice-Hall. 1980
Freeze, R. A., and J. A. Cherry. Groundwater. Prentice-Hall. 1979
Gelhar, L. W., C. Welty, and K. R. Rehfeldt. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research, 28 n.º 7: 1955-1974. 1992.
Konikow, L. F. and J. D. Bredehoeft. "Computer Model of Two-Dimensional Solute Transport and Dispersion in Ground Water", USGS Techniques of Water Resources Investigations, libro 7, cap. C2, U.S. Geological Survey, Washington, D.C. 1978.
Marsily, G. de. Quantitative Hydrogeology. Academic Press. 1986.
Tauxe, J. D. "Porous Medium Advection-Dispersion Modeling in a Geographic Information System". Tesis doctoral en ingeniería civil. University of Texas, Austin, 1994.