Disponible con una licencia de Geostatistical Analyst.
Algunos métodos de Geostatistical Analyst requieren que los datos presenten una distribución normal. Cuando los datos están sesgados (la distribución es asimétrica), es posible que le convenga transformar los datos para que sean normales. El gráfico de histograma le permite explorar los efectos de distintas transformaciones en la distribución del dataset. Si el modelo de interpolación que crea utiliza uno de los métodos de kriging y elige transformar los datos como uno de los pasos, las predicciones se transformarán de nuevo a la escala original de la superficie interpolada.
Geostatistical Analyst permite usar varias transformaciones, incluidas las de Box-Cox (también conocidas como transformaciones de potencia), arcoseno y logarítmicas. Supongamos que observa los datos Z(s) y aplica una transformación Y(s) = t(Z(s)). Normalmente, se desea hallar la transformación para que Y(s) presente una distribución normal. Lo que sucede a menudo es que la transformación también produce datos que tienen una varianza constante en el área de estudio.
Más información sobre transformaciones y tendencias
Transformación de Box-Cox
La transformación Box-Cox es
Y(s) = (Z(s)λ - 1)/λ,para λ ≠ 0.
Por ejemplo, supongamos que los datos están compuestos por recuentos de algún fenómeno. Para estos tipos de datos, la varianza a menudo está relacionada con el valor medio. Es decir, si tiene recuentos pequeños en parte de su área de estudio, la variabilidad en esa región local será menor que la variabilidad en otra región donde los recuentos sean mayores. En este caso, la transformación de raíz cuadrada puede ayudar a que las varianzas sean más constantes en toda el área de estudio y, con frecuencia, también hace que los datos aparezcan distribuidos normalmente. La transformación de raíz cuadrada es un caso especial de transformación Box-Cox cuando λ = ½.
Transformación logarítmica
La transformación logarítmica es, en realidad, un caso especial de transformación Box-Cox cuando λ = 0; la transformación es la siguiente:
Y(s) = ln(Z(s)),para Z(s) > 0, y ln es el logaritmo natural.
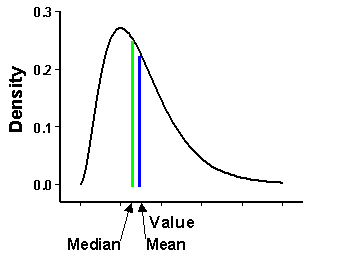
La transformación logarítmica se usa normalmente si los datos tienen una distribución sesgada de forma positiva (como se muestra a continuación) y algunos valores son muy grandes. Si estos valores grandes están en su área de estudio, la transformación logarítmica le ayudará a que las varianzas sean más constantes y normalizará sus datos. Con respecto a la terminología, cuando se implementa una transformación logarítmica con kriging, el método de predicción se conoce como kriging lognormal, mientras que para todos los demás valores de λ, el método de kriging asociado se conoce como kriging transgaussiano.
Transformación de arcoseno
A continuación, se muestra la transformación de arcoseno:
Y(s) = sin-1(Z(s)),para Z(s) entre 0 y 1.
La transformación de arcoseno se puede utilizar para datos que representan proporciones o porcentajes. Normalmente, cuando los datos son proporciones, la varianza es más pequeña cerca de 0 y 1, y más grande cerca de 0,5. La transformación de arcoseno ayuda a que las varianzas sean más constantes en toda su área de estudio y, con frecuencia, también hace que los datos aparezcan distribuidos normalmente.