Disponible con una licencia de Spatial Analyst.
El algoritmo de recorrido de partículas utilizado por la herramienta Recorrido de una partícula emplea un esquema de predicción-corrección para predecir la ubicación futura de una partícula basada en el campo de velocidad local, interpolada desde los centros de celdas ráster más cercanos y de forma similar al empleado por Konikow y Bredehoeft (1978). Las ubicaciones sucesivas de las partículas no están vinculadas a la resolución o ubicación de las celdas ráster, de modo que pueden flotar por el campo de velocidad.
Algoritmo de recorrido de partículas
Comenzando en la ubicación de origen P identificada en el archivo de recorrido, se calcula la velocidad local V a partir de las velocidades de los cuatro centros de celdas ráster más cercanos, utilizando una función de interpolación bilineal como se muestra en la siguiente imagen.
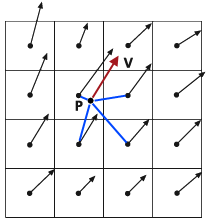
Velocidad local V calculada La determinación de la ruta se lleva a cabo mediante un método de predicción-corrección, como se ilustra en la siguiente imagen. Comenzando en el punto P, cuya ubicación es independiente de las celdas ráster, se interpola la velocidad V desde los centros de celdas vecinas y se utiliza para predecir la ubicación de la partícula P' a una distancia que especifique (este es el valor del argumento Longitud de paso).
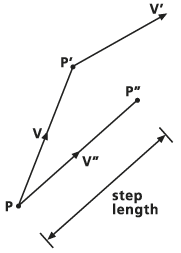
Se determina la ruta En el punto P', se interpola un nuevo vector de velocidad V' a partir de sus vecinos y se promedia con V para crear una velocidad V'' corregida. Esta velocidad corregida se utiliza para buscar una nueva ubicación P'', que se toma como punto de origen para el movimiento en el siguiente paso del recorrido. El tiempo necesario para pasar de P a P'' también se deduce del tiempo restante.
Esta técnica se aplica en sucesión (como se muestra en la imagen siguiente) hasta que el tiempo especificado caduca o la partícula migra fuera del ráster o a una depresión.
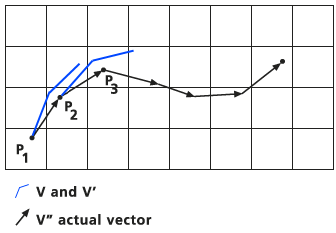
Información acumulativa registrada en el archivo de recorrido A medida que se calcula cada punto, el tiempo acumulado, la ubicación de P en x e y, la longitud acumulada y la magnitud y dirección del flujo se registran en el archivo de recorrido descrito anteriormente.
Aplicaciones
Las herramientas de agua subterránea se pueden utilizar para realizar un modelado de advección-dispersión rudimentario de los componentes del flujo de agua subterránea. Flujo Darcy genera un campo de velocidad de flujo de aguas subterráneas a partir de datos geológicos; Recorrido de una partícula sigue la ruta de advección a lo largo del campo de flujo desde un origen de punto; y Dispersión tipo puff calcula la dispersión hidrodinámica de una liberación de punto instantánea de un constituyente según sufre la advección a lo largo de la ruta del flujo. En Tauxe (1994) se presenta un análisis completo del modelado de advección-dispersión utilizando estas funciones.
La secuencia típica para modelar aguas subterráneas es realizar Flujo Darcy, después Recorrido de una partícula y, luego, Dispersión tipo puff.
Ejemplo
- A continuación, se muestra un ejemplo de la configuración del cuadro de diálogo de la herramienta Recorrido de una partícula:
Ráster de dirección de entrada: dir1
Ráster de magnitud de entrada: mag1
Coordenada X de punto de origen: 500
Coordenada Y de punto de origen: 650
Archivo de recorridos de partículas de salida : ttrack.txt
Longitud de paso: {default}
Tiempo de recorrido: {default}
Entidades de polilínea de recorrido de salida: track_feat.shp
- Como una expresión de álgebra de mapas:
ParticleTrack(dir1, mag1, ttrack.txt, 500, 650, 5, 100, track_feat.shp)
- Como una secuencia que emplea el conjunto de herramientas de modelado de agua subterránea:
out_vol = DarcyFlow(head, poros, thickn, transm, dir1, mag1) ParticleTrack(dir1, mag1, ttrack.txt, 500, 650, "#", "#", track_feat.shp) out_puff = PorousPuff(ttrack.txt, poros, thickn, 3.2e7, 50000, 6, 3, 1, 250)
Referencias
Konikow, L. F. y J. D. Bredehoeft. 1978. "Computer Model of Two-Dimensional Solute Transport and Dispersion in Ground Water". vol. 7, cap. 2 de USGS Techniques of Water Resources Investigations. Washington, D.C.: Servicio Geológico de los EE. UU.
Tauxe, J. D. 1994. "Porous Medium Advection–Dispersion Modeling in a Geographic Information System". Tesis doctoral, Universidad de Texas, Austin.