Disponible con una licencia de Geostatistical Analyst.
En términos generales, los elementos que están más cerca entre sí tienden a ser más parecidos que los que están más alejados. Este es un principio geográfico fundamental. Supongamos que usted es urbanista y tiene que construir un parque pintoresco en su ciudad. Tiene varios emplazamientos candidatos y es posible que quiera modelar las cuencas visuales en cada ubicación. Esto requerirá un dataset de superficie de elevación más detallado para su área de estudio. Supongamos que dispone de datos de elevación preexistentes para 1.000 ubicaciones de toda la ciudad. Puede utilizarlos para crear una nueva superficie de elevación.
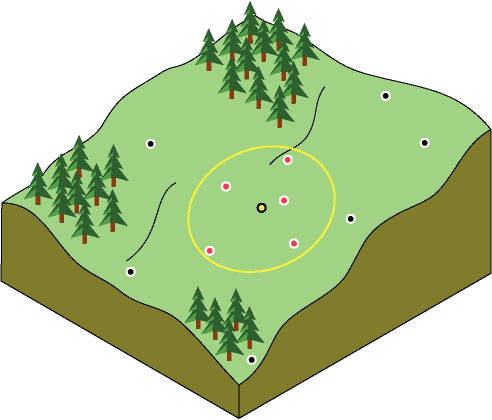
Al intentar crear la superficie de elevación, puede suponer que los valores de muestra más cercanos a la ubicación de predicción serán similares. Pero ¿cuántas ubicaciones de muestra debe tener en cuenta? ¿Se deben considerar por igual todos los valores de muestra? A medida que se aleja de la ubicación de predicción, la influencia de los puntos disminuirá. De hecho, considerar un punto demasiado lejano podría ser perjudicial porque el punto puede estar ubicado en un área que es drásticamente diferente de la ubicación de predicción.
Una solución es considerar tantos puntos como para realizar una buena predicción, pero tan pocos como para ser prácticos. El número variará con la cantidad y distribución de los puntos de muestra y el carácter de la superficie. Si las muestras de elevación están distribuidas de manera relativamente uniforme y las características de la superficie no cambian significativamente a lo largo del paisaje, se pueden predecir valores de superficie a partir de puntos cercanos con una precisión razonable. Para tener en cuenta la relación de distancia, los valores de los puntos más cercanos suelen tener una ponderación mayor que la de los más alejados. Este principio es común a todos los métodos de interpolación que se ofrecen en Geostatistical Analyst (excepto para la interpolación polinómica global, que asigna las mismas ponderaciones a todos los puntos).