Las siguientes son las distribuciones disponibles para una serie de herramientas que crean valores aleatorios. Las distribuciones transforman los valores aleatorios 0–1 creados a partir de la transmisión especificada (identificada de manera general en el entorno de análisis o de forma local en la herramienta) en la distribución establecida. Consulte la sintaxis y los parámetros de cada distribución en Sintaxis de distribución para los valores aleatorios.
Distribución uniforme
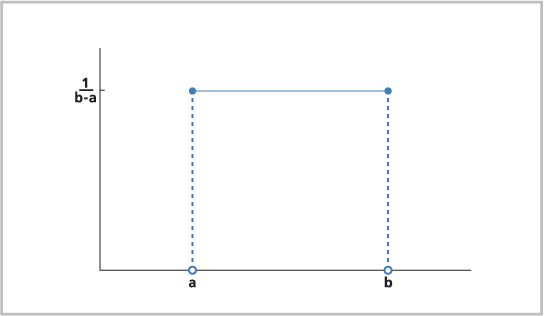
La distribución uniforme es una distribución continua de probabilidad en la que todos los valores de un intervalo especificado tienen la misma probabilidad. La distribución de enteros es una versión discreta de la distribución uniforme (consulte abajo). La distribución uniforme puede utilizarse al modelar concentraciones de un gas en un modelo de simulación o el tiempo entre accidentes en un cruce, así como para situar los puntos en la herramienta Crear puntos aleatorios.
La distribución uniforme suele utilizarse para modelar eventos aleatorios cuando cada suceso o resultado en potencia tiene la misma probabilidad de ocurrir.
La fórmula para la distribución uniforme es la siguiente:
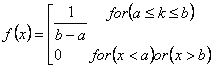
donde
a es el valor mínimo del intervalo con la misma probabilidad.
b es el valor máximo del intervalo con la misma probabilidad.
x se refiere a las observaciones.
Los valores aleatorios seleccionados están entre el mínimo y el máximo (no incluidos). El mínimo debe ser menor que el máximo. Si no se proporciona mínimo y máximo, se generan variables uniformes entre 0,0 y 1,0.
Distribución de enteros
La distribución de enteros es una distribución de probabilidad en la que todos los valores discretos de un intervalo especificado tienen la misma probabilidad. La distribución de enteros es una versión discreta de la distribución uniforme (consulte arriba). La distribución de enteros puede utilizarse para modelar la probabilidad de que salga cada número al lanzar un dado (la probabilidad de que salga un número es de una sobre seis), para modelar eventos aleatorios en un modelo de simulación o para seleccionar ubicaciones de muestreo en un estudio biológico
La distribución de enteros suele utilizarse para modelar eventos aleatorios cuando cada suceso o resultado en potencia tiene la misma probabilidad de ocurrir.

A continuación se muestra la fórmula de distribución de enteros:
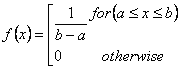
donde
a es el valor mínimo del intervalo con la misma probabilidad.
b es el valor máximo del intervalo con la misma probabilidad.
x se refiere a las observaciones.
Los valores aleatorios seleccionados están entre el mínimo y el máximo (no incluidos). El mínimo debe ser menor que el máximo. Si no se proporciona mínimo y máximo, se generan valores uniformes entre 1 y 100.
Distribución normal
La distribución normal modela las variables aleatorias continuas que ocurren normalmente. El uso de la distribución normal está muy extendido y tiene muchas aplicaciones. Se basa en el teorema central del límite, que parte del principio de que la suma de variables aleatorias se distribuye normalmente si existe un número elevado de observaciones. Por ejemplo, el número de veces que la cara aparece al lanzar varias veces una moneda se acercará a la normalidad si la moneda se lanza muchas veces. Ejemplo de la distribución normal son la altura de las personas de un país, los valores de elevación de un estado y la puntuación de los exámenes de matemáticas de todos los alumnos de 12 años.

La fórmula de la distribución normal es la siguiente:
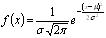
donde
μ es la media.
σ es la desviación estándar (un número positivo).
La distribución normal es simétrica con respecto a la media, el modo y la mediana, que son todas iguales en μ.
Con frecuencia, las distribuciones binomial y de Poisson modelan eventos futuros discretos, independientes, aleatorios, verdaderos o falsos (por ejemplo, el número de veces que aparece cara al lanzar una moneda) utilizando un número relativamente pequeño de observaciones, mientras que la distribución normal modela variables continuas (por ejemplo, altura, peso y cantidad) utilizando un gran número de observaciones. Las distribuciones binomial y de Poisson se basan en la probabilidad, mientras que la distribución normal es el número de observaciones que cumplen con la cantidad o la magnitud.
Distribución exponencial
La distribución exponencial es una distribución de probabilidad continua. Normalmente, se utiliza para modelar el tiempo entre eventos que ocurren con una frecuencia media constante o la distribución puede utilizarse para modelar el acontecimiento de eventos por unidad de distancia. El tiempo que pasa hasta la siguiente vez que se produce un accidente de coche en un cruce, el tiempo que transcurre entre el avistamiento de dos estrellas fugaces en el cielo nocturno y la distancia entre baches de una calle son ejemplos en los que puede utilizarse la distribución exponencial. En cada uno de estos ejemplos, a medida que aumenta el tiempo o la distancia, existe una probabilidad exponencialmente mayor de que el estado cambie o de que ocurra el evento. Las ocurrencias de los eventos son independientes entre sí.
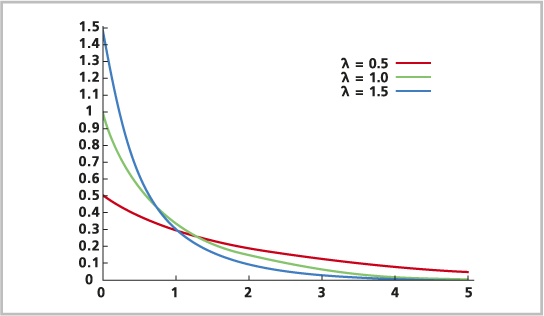
La fórmula de la distribución exponencial es la siguiente:
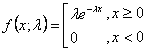
donde
e es el algoritmo natural.
x es el posible número de ocurrencias del evento (valores enteros positivos).
La distribución exponencial modela procesos de Poisson en los que el fenómeno se encuentra en un estado inicial. La distribución exponencial es la versión continua de la distribución geométrica. Si el proceso de pasar del estado A al estado B puede descomponerse en varias tareas independientes, podría ser mejor modelarlo con la distribución gamma. La distribución gamma modela la suma de varias variables independientes distribuidas exponencialmente. Puede verse como un caso especial de distribución exponencial.
Distribución de Poisson
La distribución de Poisson es una distribución de probabilidad discreta. La distribución de Poisson modela la probabilidad de que el número de eventos ocurra en un periodo de tiempo fijo dada una media conocida. Los eventos son independientes del último momento en que ocurren. En el eje x se representan los valores discretos de los eventos 0, 1, 2, 3, 4, y así sucesivamente (a menudo indicando el número de veces que ocurre el evento), y en el eje y se representa la probabilidad de que el fenómeno ocurra ese número de veces dada una media conocida. Los eventos pueden ser el número de accidentes en un cruce, el número de defectos congénitos o el número de alces en un kilómetro cuadrado. La distribución de Poisson modela sucesos poco frecuentes. La distribución a veces se denomina la ley de los pequeños números porque el evento no ocurre con frecuencia, pero existen muchas oportunidades para que suceda.

La fórmula se muestra abajo:
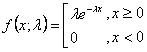
donde
e es el algoritmo natural.
k es el posible número de ocurrencias del evento (valores enteros positivos).
k! es un factorial de k.
λ (o la media) es un número positivo que representa el número previsto de ocurrencias en un intervalo concreto. Si el evento ocurre cada 10 minutos en una hora (60 minutos), el valor lambda será 6.
La distribución de Poisson es similar a la distribución binomial; sin embargo, la distribución de Poisson modela la ocurrencia de un evento poco frecuente sin necesidad de conocer información sobre el número total de posibles ocurrencias. La distribución de Poisson examina el número de accidentes en un cruce, mientras que la binomial modela el número de accidentes en relación con el número de coches que pasan por el cruce.
Distribución gamma
La distribución gamma es una distribución de probabilidad continua. La distribución gamma modela la suma de varias variables independientes distribuidas exponencialmente. Puede verse como un caso especial de distribución exponencial.

La fórmula de la distribución gamma es la siguiente:

Aquí se muestra otra forma de parametrizar la distribución gamma:

Para un alfa igual a 1, la distribución gamma equivale a la distribución exponencial. Cuando alfa es un entero, la distribución gamma se convierte en la distribución de Erlang. Para un alfa entero y un beta igual a 2, la distribución gamma se convierte en una distribución chi-cuadrado con 2 alfa grados de libertad.
Las variables resultantes son mayores o iguales que 0,0. Alfa y beta deben ser mayores que 0,0.
Distribución binomial
La distribución binomial modela el número de ocurrencias de un evento cuando se observa una secuencia de posibles generadores del evento. Por ejemplo, la distribución binomial representa el número de personas de un estudio clínico que murieron de una enfermedad cardíaca, el número de personas de un ascensor lleno que se bajan en el segundo piso o el número de animales en una población que presentan un determinado rasgo genético.
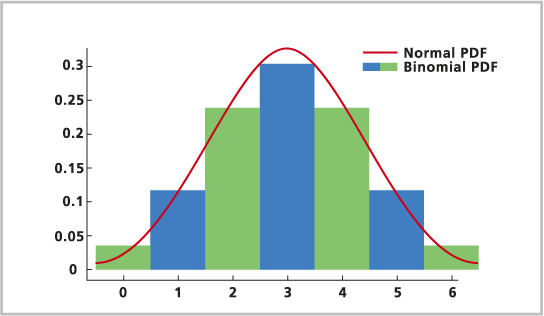
La distribución binomial describe las ocurrencias, en lugar de la magnitud. Podría modelar la cantidad de participantes que terminan una carrera, en lugar de lo rápidos que han sido.
La fórmula de la distribución binomial es la siguiente:
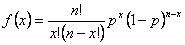
donde
n es el número de observaciones.
p es la probabilidad de que ocurra.
x es el número de éxitos de 0 a n.
Un ejemplo común de uso de la distribución binomial es la determinación de la probabilidad de que salga cara un número de veces al lanzar una moneda 10 veces (n = 10). Puede salir cara 0 veces de 10 lanzamientos, 1 de 10, y así sucesivamente; por lo tanto, x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. p es la probabilidad de cada x.
Todos los ensayos son independientes, y cada ensayo tiene un resultado de éxito o fracaso.
La distribución binomial se aproxima a la distribución de Poisson cuando n es grande y p es pequeño. En este caso, puede ser más fácil utilizar la distribución de Poisson.
La distribución binomial devuelve una variable aleatoria correspondiente al número de éxitos en n ensayos, donde la probabilidad de éxito en cada ensayo es p (por ejemplo, la probabilidad de que salga cara es p).
Distribución geométrica
La distribución geométrica es una distribución de probabilidad discreta. Existen dos tipos principales de fenómenos que modela: (1) la probabilidad del número de intentos necesarios para obtener un éxito (por ejemplo, el número de tiradas de un dado que se necesitan para sacar un 6) o (2) la probabilidad del número de fracasos antes de un éxito (por ejemplo, el número de caminatas que se requieren en un sendero antes de ver un ciervo). La probabilidad de no ver un ciervo la primera vez que se recorre un sendero es (1 - p). En la segunda caminata, la probabilidad de que no se vea un ciervo es (1 - p) (1 - p). La probabilidad de ver un ciervo aumenta exponencialmente cuantas más veces se recorre el sendero y al final se verá uno. Los eventos son independientes entre sí.

La fórmula de la distribución geometría es la siguiente:

donde
p es la probabilidad de éxito.
n es el número de ensayos.
La distribución geometría es una versión discreta de la distribución exponencial (consulte arriba). La distribución geométrica es un caso especial de distribución de Pascal o binomial negativa, con r igual a 1 en la distribución de Pascal (consulte abajo).
Distribución binomial negativa
La distribución binomial negativa es una distribución de probabilidad discreta. La distribución binomial negativa se basa en ensayos de Bernoulli. Los ensayos de Bernoulli modelan eventos en los que los intentos tienen uno de dos resultados (éxito o fracaso), presentan una probabilidad de éxito, p (siendo p la misma para cada ensayo), y son independientes entre sí. Lanzar una moneda al aire es un ensayo de Bernoulli. Por ejemplo, la distribución binomial negativa puede modelar cuántas veces hay que lanzar la moneda hasta que sale cara cinco veces seguidas. Por tanto, la distribución binomial negativa modela el número de fracasos antes de obtener un éxito. Cuando r es un entero, la distribución binomial negativa se convierte en un caso espacial conocido como distribución de Pascal.
La fórmula de la distribución binomial negativa es la siguiente:

donde
r es el número de fracasos.
p es la probabilidad de éxito.
k es el número de éxitos de 0 a n.
Cuando la distribución binomial negativa representa el lanzamiento de una moneda, se devuelve un valor aleatorio en lo que respecta a la cantidad de lanzamientos que se requieren para que salga cara.