Disponible con una licencia de Spatial Analyst.
La herramienta Estadísticas de conjunto de bandas proporciona estadísticas para el análisis multivariado de un conjunto de bandas de ráster. Cuando se habilita la opción Calcular matrices de covarianza y correlación, las matrices de covarianza y correlación son salidas, así como los parámetros estadísticos básicos, tales como los valores de la desviación mínima, máxima, media y estándar para cada capa. Cuando se habilita la opción Calcular histograma, las estadísticas del histograma se calcularán y agregarán al archivo de estadísticas de salida. Si se especifica una tabla de histograma, se creará una tabla de salida que contiene información del histograma. Si se especifica un nombre de histograma de salida, los gráficos de histograma se crearán y agregarán a la tabla de contenido.
La matriz de covarianza contiene valores de varianzas y covarianzas. La varianza es una medida estadística que muestra cuánta varianza hay desde el valor medio. Para calcular estas varianzas, se promedian los cuadrados de las diferencias entre cada valor de celda y el valor medio de todas las celdas. Las varianzas para cada capa se pueden leer a lo largo de la diagonal de la matriz de covarianza desde la parte superior izquierda hasta la inferior derecha. Las varianzas se expresan en unidades de valor de celda al cuadrado.
Las entradas restantes dentro de la matriz de covarianza son las covarianzas entre todos los pares de rásteres de entrada. La siguiente fórmula se utiliza para determinar la covarianza entre las capas i y j:
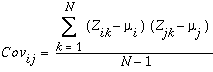
donde:
Z: valor de una celda
i, j: son las capas de una pila
µ: es el valor medio de una capa
N: es el número de celdas
k: denota una celda en particular
La covarianza de dos capas es la intersección de la fila y la columna apropiadas. La covarianza entre las capas 2 y 3 es la misma que la covarianza entre las capas 3 y 2. Los valores de la matriz de covarianza dependen de las unidades de valor, mientras que los valores de la matriz de correlación no lo dependen.
La matriz de correlación muestra los valores de los coeficientes de correlación que representan la relación entre dos datasets. En el caso de un conjunto de capas ráster, la matriz de correlación presenta los valores de celda de una capa ráster a medida que se relacionan con los valores de celda de otra capa. La correlación entre dos capas es una medida de dependencia entre las capas. Es la relación de la covarianza entre las dos capas dividida por el producto de sus desviaciones estándar. Como es una relación, es un número sin unidades. La ecuación para calcular la correlación es la siguiente:

La correlación oscila entre +1 y -1. Una correlación positiva indica una relación directa entre dos capas: por ejemplo, cuando los valores de celda de una capa aumentan, es probable que los valores de celda de otra capa también aumenten. Una correlación negativa significa que una variable cambia inversamente a la otra. Una correlación de cero significa que dos capas son independientes entre sí.
La matriz de correlación es simétrica. Su diagonal desde la parte superior izquierda a la inferior derecha es 1.0000, dado que el coeficiente de correlación de las capas idénticas es +1.
Ejemplos de archivo de estadísticas de salida
El archivo de estadísticas de salida admiten dos formatos de salida: el formato de valores separados por comas (CSV) o el formato Markdown. Los siguientes son ejemplos de los archivos de estadísticas de salida de estos formatos correspondientes a un ráster de entrada de cuatro bandas.
Salida CSV
Cuando el archivo de estadísticas de salida se especifica como un archivo de texto (con extensión de archivo .txt, .csv o .asc), se guardará en formato de valores separados por comas (CSV), lo que permitirá importarlo en otro software (como Excel) para realizar un análisis o visualización adicional.
El siguiente es el contexto de un archivo de texto creado con la opción Calcular matrices de covarianza y correlación y la opción Calcular histograma deshabilitadas. Las rutas de los datos de origen de las capas de entrada aparecen en la parte superior del archivo.
Output Band Collection Statistics Input Layers Layer,Path Layer_1,C:\example\mb_data.tif\Band_1 Layer_2,C:\example\mb_data.tif\Band_2 Layer_3,C:\example\mb_data.tif\Band_3 Layer_4,C:\example\mb_data.tif\Band_4 Statistics of Individual Layers Layer,Min,Max,Mean,Std. Dev. 1,48.00000,255.00000,73.70110,11.90945 2,22.00000,255.00000,33.73108,7.49241 3,17.00000,255.00000,31.77404,11.40892 4,13.00000,255.00000,82.51136,17.67144
Salida de markdown
El archivo de estadísticas de salida se guardará con un formato markdown si la extensión de archivo se especifica como .md.
El siguiente es el contexto de un archivo Markdown creado con la opción Calcular matrices de covarianza y correlación habilitada y la opción Calcular histograma deshabilitada cuando se visualiza como archivo de texto sin formato.
# Output Band Collection Statistics ### Input Layers | Layer | Path | | ------: | ----------------------------: | | Layer_1 | C:\example\mb_data.tif\Band_1 | | Layer_2 | C:\example\mb_data.tif\Band_2 | | Layer_3 | C:\example\mb_data.tif\Band_3 | | Layer_4 | C:\example\mb_data.tif\Band_4 | ### Statistics of Individual Layers | Layer | Min | Max | Mean | Std. Dev. | | ----: | -------: | --------: | -------: | --------: | | 1 | 48.00000 | 255.00000 | 73.70110 | 11.90945 | | 2 | 22.00000 | 255.00000 | 33.73108 | 7.49241 | | 3 | 17.00000 | 255.00000 | 31.77404 | 11.40892 | | 4 | 13.00000 | 255.00000 | 82.51136 | 17.67144 | ### Covariance Matrix | Layer | 1 | 2 | 3 | 4 | | ----: | --------: | --------: | --------: | --------: | | 1 | 141.83498 | 86.72548 | 131.13040 | -54.33298 | | 2 | 86.72548 | 56.13628 | 84.01048 | -24.88371 | | 3 | 131.13040 | 84.01048 | 130.16340 | -53.35075 | | 4 | -54.33298 | -24.88371 | -53.35075 | 312.27971 | ### Correlation Matrix | Layer | 1 | 2 | 3 | 4 | | ----: | -------: | -------: | -------: | -------: | | 1 | 1.00000 | 0.97193 | 0.96509 | -0.25817 | | 2 | 0.97193 | 1.00000 | 0.98280 | -0.18794 | | 3 | 0.96509 | 0.98280 | 1.00000 | -0.26462 | | 4 | -0.25817 | -0.18794 | -0.26462 | 1.00000 |
Salida de markdown tras la representación en pantalla
El siguiente es un ejemplo del aspecto que tiene un archivo de salida en formato markdown tras la representación en pantalla. Este archivo de salida se crea con la opción Calcular histograma habilitada y la opción Calcular matrices de covarianza y correlación deshabilitada.

Recursos adicionales
Consulte lo siguiente para más información:
Snedecor, G. W. y W. G. Cochran. 1968. Statistical Methods, 6.ª ed. Ames, Iowa: The Iowa State University Press.