Los datos ráster se obtienen de muchas fuentes, como las imágenes de satélite, las cámaras aéreas y los mapas escaneados. Las imágenes de satélite modernas y las cámaras aéreas suelen tener una información de ubicación relativamente exacta, pero pueden requerir pequeños ajustes para alinear todos los datos SIG. Los mapas digitalizados y los datos históricos no contienen normalmente información de referencia espacial. En estos casos, tendrá que usar datos de ubicación exactos para alinear o georreferenciar los datos ráster en un sistema de coordenadas de mapa. Un sistema de coordenadas de mapa se define mediante una proyección de mapa, un método por el cual la superficie curva de la Tierra se representa en una superficie plana.
Cuando realiza una georreferenciación de los datos ráster, el usuario define su ubicación mediante coordenadas de mapa y asigna el sistema de coordenadas del marco del mapa. La georreferenciación de datos ráster permite visualizarlos, consultarlos y analizarlos con otros datos geográficos. Las herramientas de georreferenciación de la pestaña Georreferencia permiten georreferenciar cualquier dataset ráster.
En general, hay cuatro pasos para georreferenciar los datos:
- Agregue el dataset ráster que desea alinear con sus datos proyectados.
- Use la pestaña Georreferencia para crear puntos de control con el fin de conectar el ráster con posiciones conocidas en el mapa.
- Revise los puntos de control y los errores.
- Guarde el resultado de georreferenciación cuando esté satisfecho con la alineación.
Alinear el ráster con puntos de control
Normalmente, georreferenciará su datos ráster usando datos espaciales existentes (datos de destino), como rásteres georreferenciados o una clase de entidad vectorial que reside en el sistema de coordenadas del mapa deseado. El proceso implica la identificación de una serie de puntos de control del terreno, conocidos como coordenadas x,y, que vinculan ubicaciones del dataset ráster con ubicaciones de los datos referenciados espacialmente. Los puntos de control son ubicaciones que se pueden identificar con precisión en el dataset ráster y en coordenadas del mundo real. Se pueden utilizar muchos tipos distintos de entidades como ubicaciones identificables, por ejemplo intersecciones de corrientes o caminos, afloramientos de roca, el extremo de una punta de tierra, la esquina de un campo establecido, esquinas de calles o la intersección de dos setos.
Los puntos de control se utilizan en combinación con la transformación para desplazar y combar el dataset ráster desde la ubicación existente a la ubicación espacialmente correcta. La conexión entre un punto de control del dataset ráster (el punto de partida) y el punto de control correspondiente de los datos de destino alineados (el punto de destino) es un par de puntos de control.
El número de vínculos que necesita crear depende de la complejidad de la transformación que piensa utilizar para transformar el dataset ráster en coordenadas de mapa. Sin embargo, la adición de más vínculos no resultará necesariamente en un mejor registro. Si es posible, debería expandir los vínculos por todo el dataset ráster en lugar de concentrarlos en un área. Normalmente, tener al menos un vínculo junto a cada esquina del dataset ráster y unos cuantos por el interior genera los mejores resultados.
Generalmente, cuanto mayor sea la superposición entre el dataset ráster y los datos de destino, mejor será la alineación, porque tendrá puntos más espaciados con los que georreferenciar el dataset ráster. Por ejemplo, si sus datos de destino solo ocupan un cuarto del área de su dataset ráster, los puntos que podría utilizar para alinear el dataset ráster se confinarían a esa área de superposición. Así, no es probable que las áreas situadas fuera del área de superposición se alinearan correctamente. Tenga en cuenta que sus datos georreferenciados solo son tan precisos como los datos con los que se alinean. Para minimizar errores, debería georreferenciar a datos de la máxima resolución y la escala más grande para sus necesidades.
Transformar el ráster
Cuando haya creado suficientes puntos de control, podrá transformar el dataset ráster a las coordenadas de mapa de los datos de destino. Tiene la opción de utilizar varios tipos de transformaciones, como las de polinomio, de spline, de ajuste, proyectiva o de similitud, para determinar la ubicación correcta de las coordenadas de mapa para cada celda del ráster.
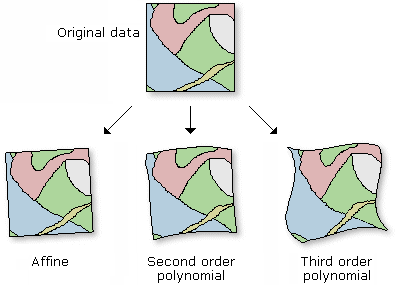
La transformación polinómica utiliza un polinomio basado en puntos de control y un algoritmo de adecuación por mínimos cuadrados (LSF). Está optimizada para la precisión global, pero no garantiza la precisión local. La transformación polinómica produce dos fórmulas: una para calcular la coordenada X de salida de una ubicación de entrada (X, Y) y una para calcular la coordenada Y de una ubicación de entrada (X, Y). El objetivo del algoritmo de adecuación por mínimos cuadrados es derivar una fórmula general que se pueda aplicar a todos los puntos, normalmente a costa de un ligero movimiento de las posiciones de los puntos de control. La cantidad de puntos de control no correlativos requerido para este método debe ser de 1 para un cambio de orden cero, 3 para un primer orden afín, 6 para un segundo orden y 10 para un tercer orden. Los polinomios del menor orden tienden a generar un error de tipo aleatorio, mientras que los polinomios de mayor orden tienden a generar un error de extrapolación.
Un polinomio de orden cero se utiliza para convertir los datos. Esto se utiliza generalmente cuando los datos ya están georreferenciadas, pero un pequeño cambio alinea mejor los datos. Solo se necesita un punto de control para realizar un cambio con polinomio de orden cero. Podría ser una buena idea crear unos cuantos puntos de control y luego elegir el que parezca ser el más preciso.
La transformación polinómica de primer orden se utiliza normalmente para georreferenciar una imagen. Utilice una transformación afín de primer orden para desplazar, escalar y girar un dataset ráster. Esto normalmente da lugar a líneas rectas en el dataset ráster representadas como líneas rectas en el dataset ráster combado. Así, los cuadros y los rectángulos del dataset ráster se suelen cambiar a paralelogramos de ajuste de escala arbitraria y orientación angular. A continuación se muestra la ecuación para transformar un dataset ráster utilizando la transformación polinomial afín (primer orden). Puede ver cómo seis parámetros definen cómo se transforman las filas y columnas de un ráster en coordenadas de mapa.
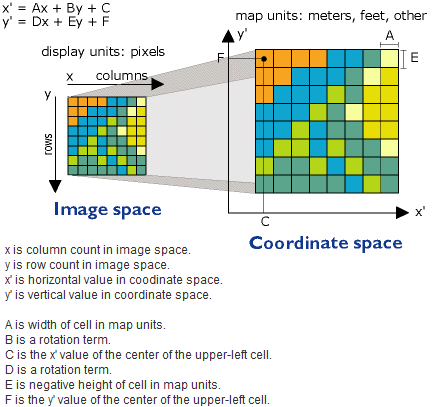
Con un mínimo de tres puntos de control, la ecuación matemática utilizada con una transformación de primer orden puede asignar exactamente cada punto ráster a la ubicación de destino. La presencia de más de tres puntos de control introduce errores, o errores residuales, que se distribuyen por todos los puntos de control. Sin embargo, debería agregar más de tres puntos de control, porque si un control no es preciso, tiene un impacto mucho mayor en la transformación. Así, aunque el error de transformación matemática pueda aumentar al crear más vínculos, la precisión general de la transformación también aumentará.
Cuanto mayor sea el orden de la transformación, más compleja será la distorsión que se puede corregir. Sin embargo, raramente se necesitan transformaciones de más de tercer orden. Las transformaciones de orden superior necesitan más vínculos y, por tanto, implican más tiempo de procesamiento. En general, si es necesario extender, escalar y girar su dataset ráster, utilice una transformación de primer orden. No obstante, si tiene que doblar o curvar el dataset ráster, utilice una transformación de segundo o tercer orden.
La transformación de ajuste optimiza el LSF global y la precisión local. Se basa en un algoritmo que combina una transformación polinómica y técnicas de interpolación de red irregular de triángulos (TIN). La transformación de ajuste realiza una transformación polinómica mediante dos conjuntos de puntos de control y ajusta los puntos de control de forma local para combinar mejor los puntos de control de destino mediante una técnica de interpolación de TIN. Necesita un mínimo de tres puntos de control.
La transformación de similitud es una transformación de primer orden que intenta conservar la forma del ráster original. El error RMS tiende a ser superior que el de otras transformaciones polinómicas dado que preservar la forma es más importante que conseguir el mejor ajuste. Del mismo modo, necesita un mínimo de tres puntos de control.
La transformación proyectiva puede combar líneas de manera que permanezcan rectas. Al hacerlo, es posible que las líneas que una vez fueron paralelas ya no sigan siendo paralelas. La transformación proyectiva es especialmente útil para imágenes oblicuas, mapas escaneados y para algunos productos de imágenes como Landsat y Digital Globe. Se requiere un mínimo de cuatro vínculos para realizar una transformación proyectiva. Cuando se utilizan solo cuatro vínculos, el error RMS será cero. Cuando se utilizan más puntos, el error RMS estará ligeramente por encima de cero. La transformación proyectiva necesita un mínimo de cuatro puntos de control.
La transformación por spline es un verdadero método de deformación elástica vectorial y optimiza para la exactitud local, pero no para la global. Se basa en una función por spline, un polinomio por partes que mantiene la continuidad y la suavidad entre los polinomios adyacentes. Las transformaciones por spline transforman los puntos de control de origen exactamente en puntos de control de destino; no se garantiza que los píxeles que están a una distancia de los puntos de control sean precisos. Esta transformación es útil cuando los puntos de control son importantes y se necesita que se registren de forma precisa. La adición de más puntos de control puede aumentar la precisión general de la transformación por spline. Ésta necesita un mínimo de 10 puntos de control.
Interpretar el error cuadrático medio
Cuando la fórmula general se deriva y se aplica al punto de control, se devuelve una medida del error residual. El error es la diferencia entre dónde terminó el punto de partida y la ubicación real especificada. El error total se calcula mediante la suma cuadrática media (RMS) de todos los errores residuales para calcular el error RMS. Este valor describe el grado de coherencia de la transformación entre los distintos puntos de control. Cuando el error es especialmente grande, puede quitar y agregar puntos de control para ajustarlo.
Aunque el error RMS es una buena evaluación de la precisión de la transformación, no confunda un error RMS bajo con un registro preciso. Por ejemplo, la transformación todavía puede contener errores considerables debido a un punto de control mal introducido. Cuantos más puntos de control de calidad equivalente se utilicen, más preciso será el polinomio a la hora de convertir los datos de entrada en coordenadas de salida. Normalmente, las transformaciones por spline y de ajuste dan un error cuadrático medio prácticamente igual a cero; sin embargo, esto no significa que la imagen se georreferencie perfectamente.
El residual hacia adelante le muestra el error en las mismas unidades que la referencia espacial del marco de datos. El residual inverso muestra el error en las unidades de píxeles. El residual inverso hacia adelante es una medida de qué tan cercana está su exactitud, medida en píxeles. Todos los valores residuales más cercanos a cero se consideran más precisos.
Conservar la información de georreferenciación
Puede transformar permanentemente el dataset ráster después de georreferenciarlo utilizando el comando Guardar en nuevo de la pestaña Georreferenciar o usando la herramienta Combar. También puede almacenar la información de transformación en los archivos auxiliares usando el comando Guardar de la pestaña Georreferencia.
Guardar en nuevo o la herramienta de geoprocesamiento Combar creará un nuevo dataset ráster que se georreferencia usando las coordenadas del mapa y la referencia espacial. ArcGIS no requiere que transforme permanentemente el dataset ráster para mostrarlo con otros datos espaciales; sin embargo, debe hacerlo si desea realizar un análisis con él o si desea utilizarlo con otro paquete de software que no reconozca la información de georreferenciación externa creada en el archivo de georreferenciación.
Al guardar la georreferenciación, se almacenará la información de transformación en archivos externos, no se creará un nuevo dataset ráster, lo que sí sucede cuando se transforma permanentemente un dataset ráster. Para un dataset ráster que está basado en archivo, como un TIFF, la transformación por lo general se almacenará en un archivo XML que tenga una extensión .aux.xml. Si el dataset ráster es una imagen sin procesar, como BMP, y la transformación es afín, se escribirá en un archivo de georreferenciación. Para un dataset ráster en una geodatabase, Guardar almacenará la transformación de geodatos en un archivo auxiliar interno del dataset ráster.