La herramienta Asignar pesos por comparación por pares calcula los pesos relativos para un conjunto de variables de entrada comparándolas por pares. Se proporciona una función de diagnóstico para garantizar que las evaluaciones de comparación entre todos los pares sean lógicamente consistentes. La herramienta calcula la relación de consistencia (RC) para ayudarle a mejorar la consistencia de sus evaluaciones. Por ejemplo, sus evaluaciones por pares serán inconsistentes si clasifica la variable A como dos veces más importante que la variable B, clasifica la variable B como dos veces más importante que la variable C y clasifica la variable C con la misma importancia que la variable A. Es decir, si A > B y B > C, entonces C no puede ser igual a A.
Mantener la RC dentro de límites aceptables ayuda a evitar clasificaciones inconsistentes. De acuerdo con Saaty (2000):
- Si la RC <= 0,1, la consistencia de la comparación por pares es aceptable.
- Si la RC > 0,1, las evaluaciones de comparación deben ajustarse para mejorar la consistencia.
Proceso de cálculo de la relación de consistencia
Los pasos para calcular la RC son los siguientes:
- Se calcula el índice de consistencia (IC).
- El índice aleatorio (IA) se determina en función del número de variables.
- La RC se calcula dividiendo el IC entre el IR.
La siguiente matriz de comparación se utilizará en un ejemplo que demuestra cómo se calcula la RC para cinco variables.
| Variable | Solar_Gain | Orientación | Elevación | Dist_to_Road | Dist_to_Elect | Pesos |
|---|---|---|---|---|---|---|
Solar_Gain | 1 | 3 | 2 | 2 | 0,333 | 0,235 |
Orientación | 0,333 | 1 | 0,5 | 1 | 0,2 | 0,089 |
Elevación | 0,5 | 2 | 1 | 1 | 0,5 | 0,136 |
Dist_to_Road | 0,5 | 1 | 1 | 1 | 5 | 0,247 |
Dist_to_Elect | 3 | 5 | 2 | 0,2 | 1 | 0,294 |
En los cálculos se utiliza la serie de ecuaciones que se describe a continuación.
Calcular el IC
El IC se calcula utilizando la siguiente fórmula:
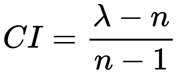
Donde:
- λ (el valor propio principal) es la media de los λi para cada variable
- n es el número de variables de entrada
El valor λi para cada variable se calcula utilizando la siguiente fórmula:

Donde:
- wi denota los pesos derivados para cada variable de entrada (la columna Pesos en la Tabla 1)
- SWi es la suma ponderada para cada variable i
La suma ponderada para cada variable se calcula utilizando la siguiente fórmula:

Donde:
- aij es el valor de la matriz de comparación por pares original, donde i se refiere a la fila y j se refiere a la columna
- wj son los pesos derivados de las variables correspondientes
Por ejemplo, la SW para la fila de la variable Solar_Gain se calcula de la siguiente manera:

El λi para la variable Solar_Gain se calcula de la siguiente manera:

Repita los cálculos para cada fila para encontrar el valor λi para cada variable.
A continuación, promedie los valores λi para obtener λ.
En este ejemplo, λ es 6,462 como se especifica en la siguiente tabla.
| Variable | Pesos(wi) | Suma ponderada(SWi) | λi = SWi / wi |
|---|---|---|---|
Solar_Gain | 0,235 | 1,366 | 5,812 |
Orientación | 0,089 | 0,541 | 6,079 |
Elevación | 0,136 | 0,826 | 6,070 |
Dist_to_Road | 0,247 | 2,060 | 8,338 |
Dist_to_Elect | 0,294 | 1,765 | 6,005 |
Media | NA | NA | 6,462 |
Con λ ahora calculado, el IC se puede calcular utilizando la fórmula proporcionada anteriormente.
Dado que el número de variables en este ejemplo es cinco, el valor del IC se calcula de la siguiente manera:
IC = (6,462 - 5)/(5 - 1) = 0,365Calcular el IR
El IR es un valor estadístico predefinido que ofrece un punto de referencia para calcular el IC para las comparaciones por pares. Desarrollados por Saaty (2000), los valores de IR se derivan de una simulación de Monte Carlo para cada tamaño de matriz. Los valores de IR derivados para cada tamaño de matriz se muestran en la tabla siguiente. Los tamaños de matriz se identifican en la fila superior.
| Tamaño de la matriz | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
IR | 0 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 |
El valor del IR es 0 para la comparación de dos variables porque la comparación es inherentemente consistente. Los valores del IR aumentan con el número de variables de entrada.
En este ejemplo, el número de variables es cinco, por lo que el valor del IR correspondiente es 1,12.
Calcular la RC
La RC se calcula dividiendo el IC entre el IR. Este valor de RC muestra la consistencia de las comparaciones por pares.
En este ejemplo, la CR se calcula de la siguiente manera:
RC = 0,365/1,12 = 0,326Dado que el valor de la RC es mayor que 0,1, debe modificar las evaluaciones de comparación para mejorar la consistencia.
Mejorar la consistencia
Si se determina que las comparaciones de las variables de entrada son inconsistentes, se resaltan los tres pares que más contribuyen a la inconsistencia. Los pares resaltados deben ajustarse para mejorar la consistencia.
El flujo de trabajo que se muestra a continuación se utiliza para determinar los tres pares más inconsistentes.
Construir una matriz de consistencia por pares
Construya una matriz que se utilizará en la evaluación de la consistencia por pares (Saaty, 2003). Esta matriz se denomina εij en la siguiente fórmula:

Donde:
- aij es el valor de la matriz de comparación por pares original, i se refiere a la fila y j se refiere a la columna.
- wj y wi son los pesos derivados para las variables j e i.
Calcular los valores
Una vez construida la matriz, se identifican los tres valores más grandes en la matriz εij. Las variables de fila y columna correspondientes se consideran pares inconsistentes.
En este ejemplo de comparación, el valor de la RC es mayor que 0,1 (0,326). Para identificar los pares inconsistentes, el valor εij para la fila Solar_Gain y la celda de columna Orientación se calcula de la siguiente manera:

Repita el cálculo para todas las celdas.
Determinar los pares más inconsistentes
La matriz εij para el ejemplo de comparación anterior se construye de la siguiente manera:
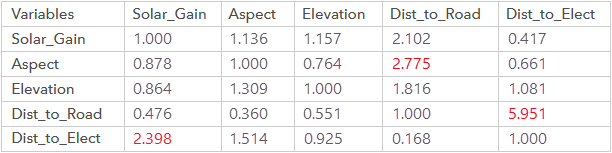
Los tres valores más altos de la matriz son las comparaciones que más contribuyen a la inconsistencia. Son las evaluaciones de comparación para las variables Dist_to_Road y Dist_to_Elect, para las variables Orientación y Dist_to_Road, y para las variables Dist_to_Elect y Solar_Gain. Los tres pares están resaltados en rojo a ambos lados de los controles deslizantes en el cuadro de diálogo de la herramienta.
En la matriz de comparación original, la variable Solar_Gain se evalúa como dos veces más importante que Dist_to_Road (Solar_Gain > Dist_to_Road), y tres veces menos importante que Dist_to_Elect (Dist_to_Elect > Solar_Gain). Lógicamente, Dist_to_Road debería ser menos importante que Dist_to_Elect (Dist_to_Elect > Dist_to_Road). Sin embargo, en la comparación original, la evaluación asignó incorrectamente a Dist_to_Road una ponderación cinco veces más importante que Dist_to_Elect (Dist_to_Road > Dist_to_Elect). Esta es una de las principales causas de la inconsistencia.
Para corregirlo, mueva el control deslizante hacia el lado Dist_to_Elect y revise de nuevo la RC. Por ejemplo, si mueve el control deslizante a la posición 5 en el lado Dist_to_Elect y hace clic de nuevo en el botón Consistencia, la nueva RC es 0,029, lo que indica que la comparación general es ahora consistente.
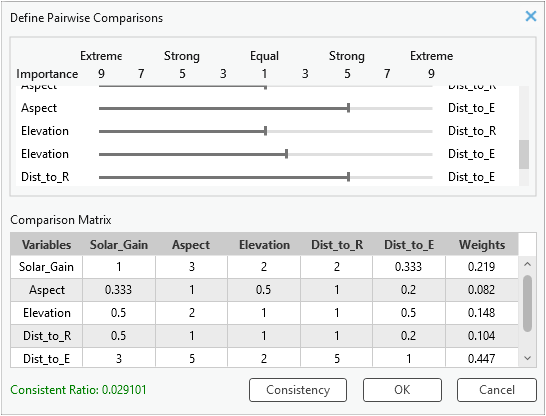
Referencias
Saaty, T. L. 2000. Fundamentos de la toma de decisiones y teoría de las prioridades con el proceso de jerarquía analítica (AHP). Pittsburgh, PA: RWS Publications
Saaty, T. L. 2003. «Toma de decisiones con el AHP: ¿Por qué es necesario el vector propio principal?». European Journal of Operational Research, 145(1), 85-91.