Disponible avec une licence Spatial Analyst.
L’outil Composantes principales permet de convertir des données dans des canaux en entrée dans l’espace attributaire multivarié lorsque vous faites pivoter les axes par rapport à l’espace d’origine. Les axes (attributs) du nouvel espace ne sont pas corrélés. La raison principale de transformer les données dans une analyse des composants principale est de compresser des données en éliminant la redondance.
Il est évident que les données sont redondantes dans un raster multicanal comprenant des valeurs d'altitude, de pente et d'exposition (sur une échelle continue). Etant donné que la pente et l'exposition sont généralement dérivées de l'altitude, une grande proportion de la variance peut s'expliquer, dans la zone d'étude, par l'altitude.
Le résultat est un raster multicanal ayant le même nombre de canaux que les composants désignés (un canal par axe dans le nouvel espace multivarié). La première composante principale aura la variance la plus élevée, la deuxième variance la plus élevée qui n'est pas décrite par la première, et ainsi de suite. Souvent, les trois (ou quatre) premiers rasters issus du raster multicanal généré avec l’outil Composantes principales peuvent décrire plus de 95 % de la variance. Vous pouvez supprimer les canaux individuels restants. Dans la mesure où le nouveau raster contient moins de couches et plus de 95 % de la variance du raster d'origine, les calculs sont plus rapides et la précision est conservée.
L’outil Composantes principales nécessite un raster multicanal en entrée, le nombre de composantes principales pour convertir les données, le nom du fichier de statistiques en sortie et le nom du raster en sortie. Le raster en sortie comprend le même nombre de canaux que le nombre de composantes défini. Chaque canal décrit une composante.
Concepts d'analyse en composantes principales
Théoriquement, en utilisant un raster à deux canaux, le décalage, la rotation des axes et la transformation des données sont effectués comme suit :
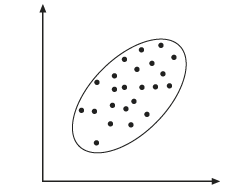
- Les données sont tracées dans un diagramme à nuage de points.
- Une ellipse est calculée pour lier les points contenus dans le nuage de points (voir la figure ci-dessous).
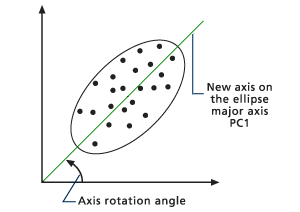
Limite d'ellipse tracée - Le grand axe de l'ellipse est indiqué (voir la figure ci-dessous). Le grand axe devient le nouvel axe des x, la première composante principale (PC1). PC1 décrit la variance la plus importante car elle représente la plus grande section transversale à travers l'ellipse. La direction de PC1 est le vecteur propre, et sa grandeur la valeur propre. L'angle de l'axe des x par rapport à PC1 est l'angle de rotation utilisé dans la transformation.
Première composante principale - Le système calcule une ligne perpendiculaire à la ligne orthogonale PC1. Cette ligne est la deuxième composante principale (PC2) et le nouvel axe pour l'axe des y d'origine (voir la figure ci-dessous). Le nouvel axe décrit la deuxième variance la plus importante qui n’apparaît pas dans PC1.
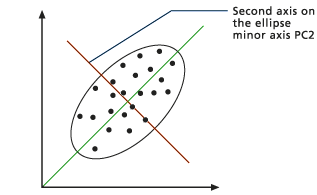
Deuxième composante principale
A l'aide des vecteurs propres, des valeurs propres et de la matrice de covariance calculée de l'entrée du raster multicanal, une formule linéaire définissant le décalage et la rotation est créée. Cette formule est appliquée pour transformer chaque valeur de cellule par rapport au nouvel axe.
Exemple
Voici un exemple de fichier de données en sortie créé pour trois composants principaux :
COVARIANCE MATRIX # Layer 1 2 3 # ----------------------------------------------------------- 1 34.1763 31.2377 51.8100 2 31.2377 212.6159 99.9540 3 51.8100 99.9540 118.8057 # =========================================================== # CORRELATION MATRIX # Layer 1 2 3 # ----------------------------------------------------------- 1 1.0000 0.3665 0.8131 2 0.3665 1.0000 0.6289 3 0.8131 0.6289 1.0000 # =========================================================== # EIGENVALUES AND EIGENVECTORS # Number of Input Layers Number of Principal Component Layers 3 3 # PC Layer 1 2 3 # ----------------------------------------------------------- # Eigen Values 287.8278 69.8781 7.8920 # Eigen Vectors # Input Layer 1 0.2112 0.4718 0.8560 2 0.8116 -0.5727 0.1154 3 0.5447 0.6704 -0.5039 # ===========================================================
Bibliographie
Campbell, James B. Introduction to Remote Sensing. The Guilford Press. 1987.
Jensen, John R. Introductory Digital Image Processing : A Remote Sensing Perspective. Prentice–Hall. 1986.
Lillesand, Thomas M., and Ralph W. Kiefer. Remote Sensing and Image Processing. John Wiley and Sons. 1987.
Richards, John A. Remote Sensing Digital Image Analysis : An Introduction. Berlin : Springer-Verlag. 1986.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?