La tendance pour un ensemble d'entités linéaires est mesurée en calculant l'angle moyen des lignes. La statistique utilisée pour calculer la tendance porte le nom de moyenne directionnelle. La statistique elle-même est appelée moyenne directionnelle, mais elle permet de mesurer une direction ou une orientation.
De nombreuses entités linéaires pointent dans une direction ; elles ont un point de départ et un point d'arrivée. Ces lignes représentent souvent les trajectoires d'objets en mouvement, tels que des ouragans. D'autres entités linéaires, telles que les lignes de faille, n'ont ni point de départ ni point d'arrivée. Ces entités sont considérées avoir une orientation mais pas de direction. Par exemple, une ligne de faille peut avoir une orientation nord-ouest/sud-est. L'outil Direction moyenne linéaire permet de calculer la direction moyenne ou l'orientation moyenne d'un ensemble de lignes.
Mesure de la direction ou de l'orientation
Dans un SIG, chaque ligne dispose d'un point de départ, d'un point d'arrivée et d'une direction. La direction est définie lorsque l'entité linéaire est créée par numérisation ou importation d'une liste de coordonnées. Vous pouvez voir la direction de chaque ligne en l'affichant avec un symbole de pointe de flèche. Si vous calculez la direction moyenne, veillez à ce que les directions des lignes soient correctes. Si vous calculez l'orientation moyenne, la direction des lignes est ignorée.
La direction moyenne est calculée pour des entités qui se déplacent d'un point de départ à un point d'arrivée, telles que des tempêtes, alors que l'orientation moyenne est calculée pour des entités stationnaires, telles que des lignes de faille. Dans certaines situations, il peut s'avérer nécessaire de calculer l'orientation moyenne des lignes qui représentent le mouvement. Un biologiste de la faune sauvage qui s'intéresse aux points de départ et d'arrivée de la migration saisonnière des wapitis peut calculer la direction moyenne des chemins pris par les wapitis pendant chaque saison. Toutefois, ce biologiste calculerait l'orientation moyenne s'il s'intéressait aux caractéristiques des itinéraires de migration proprement dits pour déterminer ce qui qualifie un bon itinéraire, plutôt qu'aux points de départ et d'arrivée des wapitis. Le biologiste pourrait calculer l'orientation moyenne à l'aide des chemins des wapitis dans les deux directions (aller et retour) et capturer plus d'informations sur leurs déplacements.
N'oubliez pas que même si la plupart des lignes présentent de nombreux sommets entre le point de départ et le point d'arrivée, cet outil n'utilise que ces deux points pour déterminer la direction.
Calculs

Sortie
L'outil Direction moyenne linéaire crée une nouvelle classe d'entité en sortie qui contient une entité linéaire centrée sur le centre moyen pour tous les centroïdes vectoriels en entrée, avec une longueur égale à la longueur moyenne de tous les vecteurs en entrée et avec l'orientation moyenne ou la direction moyenne de tous les vecteurs en entrée. Les valeurs attributaires pour les nouvelles entités linéaires comprennent l'angle horizontal (dans le sens horaire à partir du Nord), la moyenne directionnelle (dans le sens anti-horaire à partir de l'Est), la variance circulaire (indication de la quantité de directions ou d'orientations de lignes qui dévient de la moyenne directionnelle), les coordonnées X et Y du centre moyen et la longueur moyenne.
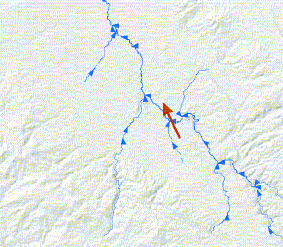
Applications possibles
- Comparaison de deux ensembles de lignes ou plus : par exemple, un biologiste de la faune sauvage qui étudie le mouvement des wapitis et des élans dans une vallée fluviale pourrait calculer la tendance directionnelle des itinéraires de migration des deux espèces.
- Comparaison d'entités pour différentes périodes : par exemple, un ornithologiste pourrait calculer la tendance de la migration des faucons mois par mois. La moyenne directionnelle résume les trajectoires de vol de plusieurs individus et élimine les mouvements journaliers par lissage. Cela permet d'observer clairement pendant quel mois les oiseaux voyagent le plus loin et quand la migration prend fin.
- Evaluation des arbres abattus dans une forêt pour comprendre les motifs et la direction du vent.
- Analyse des stries glaciaires, qui indiquent le mouvement des glaciers.
- Identification de la direction générale des vols de voitures et des récupérations de véhicules volés.
Ressources supplémentaires
Cordeiro, Gauss M. et Silvia L. De Paula Ferrari. « A modified score test statistic having chi-squared distribution to order n −1 . » Biometrika (1991) 78 (3) : 573-582.
Mardia, K.V. et Peter E. Jupp. Statistiques directionnelles. Chichester : J. Wiley, 2000.
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
Vous avez un commentaire à formuler concernant cette rubrique ?