Lorsque que nous observons le monde qui nous entoure, nous avons naturellement tendance à organiser, grouper, différencier et cataloguer ce que nous voyons afin d'essayer de mieux le comprendre. Ce type de processus de classement mental est essentiel à l'acquisition de connaissances et à la compréhension. De même, pour mieux connaître et comprendre vos données, vous pouvez utiliser l’outil Agrégation multivariée spatialement contrainte. Selon le nombre d’agrégats à créer, il recherche une solution dans laquelle toutes les entités de chaque agrégat sont aussi similaires que possible, et où tous les agrégats sont aussi différents que possible. La similarité des entités est établie en fonction du jeu d’attributs que vous spécifiez pour le paramètre Analysis Fields (Champs d’analyse) et peut éventuellement inclure des contraintes concernant la taille des agrégats. L’algorithme utilisé par cet outil emploie un diagramme de connectivité (arbre couvrant de poids minimal) et une méthode appelée SKATER pour rechercher les agrégats naturels dans vos données ainsi que les signes d’accumulation pour évaluer la probabilité d’appartenance des agrégats.
Astuce :
Les techniques d’agrégation, de regroupement et de classification comptent parmi les méthodes les plus utilisées dans l’apprentissage automatique. L’outil Agrégation multivariée spatialement contrainte utilise des méthodes d’apprentissage automatique non assistées pour déterminer l’agrégation naturelle dans vos données. Ces méthodes de classification sont dites non assistées en ce sens qu’il est possible de les utiliser sans aucun ensemble d’entités préclassées à connaître ou auxquelles se référer pour déterminer l’agrégation de vos données.
Alors qu’il existe des centaines d’algorithmes d’analyse d’agrégat similaires, ils sont tous classés comme étant de difficulté NP. Par conséquent, la seule façon de s’assurer qu’une solution maximise parfaitement les similarités à l’intérieur des agrégats et les différences entre les agrégats consiste à essayer toutes les combinaisons possibles des entités à agréger. Si cela est possible avec quelques entités, le problème devient vite insoluble.
Il est non seulement ardu d’être certain d’avoir trouvé une solution optimale, mais il est également irréaliste d’essayer d’identifier un algorithme d’agrégation parfaitement adapté à toutes les formules de données possibles. Les agrégats ont des formes, des tailles et des densités différentes. Les données attributaires peuvent inclure diverses plages, symétries, continuités et unités de mesure. Cela explique pourquoi un si grand nombre d’algorithmes d’analyse d’agrégat ont été développés ces 50 dernières années. Il est donc plus approprié de considérer l'outil Agrégation multivariée spatialement contrainte comme un outil exploratoire qui vous permet d'acquérir des connaissances supplémentaires sur les structures sous-jacentes de vos données.
Applications possibles
Voici quelques exemples d’application de cet outil :
- Si vous avez rassemblé des données d’observation des animaux pour mieux comprendre leurs territoires, l’outil Agrégation multivariée spatialement contrainte peut être utile. Comprendre où et quand les saumons se rassemblent à différents stades de leur vie, par exemple, peut aider à créer des zones protégées afin de tenter d'optimiser leur reproduction.
- Imaginons que vous êtes un agronome et que vous voulez classer les différents types de sols de votre zone d’étude. L'exécution de l'outil Agrégation multivariée spatialement contrainte sur les caractéristiques du sol d'une série d'échantillons peut vous aider à identifier des agrégats de types de sols distincts et contigus.
- L'agrégation de clients selon leurs habitudes d'achat, leurs caractéristiques démographiques et leurs habitudes de déplacement peut vous permettre de concevoir une stratégie marketing efficace pour les produits de votre société.
- Les urbanistes doivent souvent diviser les villes en quartiers distincts pour décider de l'emplacement des équipements collectifs, promouvoir l'activisme local et la participation de la communauté. L'outil Agrégation multivariée spatialement contrainte, exécuté sur les caractéristiques physiques et démographiques des pâtés de maisons d'une ville, peut aider les urbanistes à identifier les zones de cette ville qui sont spatialement contiguës et dont les caractéristiques physiques et démographiques sont similaires.
- Le sophisme écologique est un problème connu pour l’inférence statistique chaque fois qu’une analyse est réalisée sur des données agrégées. La structure d’agrégation utilisée pour l’analyse n’a souvent aucun rapport avec ce que vous souhaitez analyser. Les données de recensement, par exemple, sont agrégées en fonction de la distribution de la population, critère qui peut ne pas être adapté à l’analyse des feux de forêts. Pour réduire le biais d’agrégation et échapper au sophisme écologique, vous pouvez utiliser une méthode efficace qui consiste à diviser les plus petites unités d’agrégation possibles en régions homogènes pour un jeu d’attributs qui se rapportent exactement aux questions analytiques posées.
Entrée(s)
Cet outil accepte des Input Features (Entités en entrée) surfaciques et ponctuelles, un chemin d’accès aux Output Features (Entités en sortie), un ou plusieurs Analysis Fields (Champs d’analyse), une valeur d’entier représentant le Number of Clusters (Nombre d’agrégats) à créer et le type de Spatial Constraint (Contrainte spatiale) à appliquer dans l’algorithme d’agrégation. Il est également possible d’utiliser un certain nombre de paramètres facultatifs pour définir les Cluster Size Constraints (Contraintes de taille d’agrégat), que ce soit pour établir un nombre minimal ou maximal d’entités par agrégat ou pour une somme minimale ou maximale de valeurs attributaires par agrégat et une Output Table for Evaluating Optimal Number of Clusters (Table de sortie pour l’évaluation du nombre optimal d’agrégats).
Champs d’analyse
Sélectionnez des champs numériques correspondants à des systèmes de mesure de ratio, d’intervalle ou ordinaux. Alors que les données nominales peuvent être représentées à l’aide de variables (binaires) fictives, elles ne fonctionnent généralement pas aussi bien que d’autres types de variables numériques. Ainsi, vous pouvez créer une variable nommée « Rural » et attribuer à chaque entité (chaque secteur de recensement, par exemple) la valeur 1 s’il s’agit d’une zone principalement rurale, ou la valeur 0 si elle est principalement urbaine. La quantité ou la proportion de terrains agricoles associée à chaque entité est une meilleure représentation de cette variable si l'on veut l'utiliser avec l'outil Agrégation multivariée spatialement contrainte.
Remarque :
Les valeurs des Analysis Fields (Champs d’analyse) sont standardisées par l’outil, car les variables à variances élevées (où les valeurs des données sont dispersées autour de la moyenne) ont généralement une plus grande influence sur les agrégats que les variables à faibles variances. La standardisation des valeurs attributaires implique une transformation z dans laquelle la moyenne de toutes les valeurs est soustraite de chaque valeur et divisée par l'écart type pour toutes les valeurs. La standardisation définit tous les attributs à la même échelle, même lorsque ceux-ci sont représentés par des types de nombres très différents : taux (chiffres de 0 à 1,0), population (avec des valeurs supérieures à un million) et distances (kilomètres, par exemple).
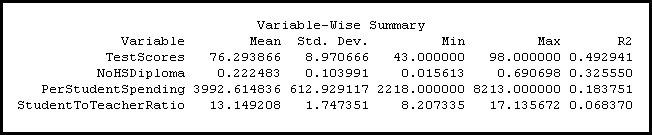
Sélectionnez des variables qui, à votre avis, permettront de distinguer les agrégats d’entités les uns des autres. Supposons, par exemple, que vous souhaitiez agréger les zones scolaires en fonction des résultats obtenus par les élèves à des tests de connaissance normalisés. Vous pourriez sélectionner des Analysis Fields (Champs d’analyse) qui incluent des résultats globaux, des résultats pour certaines matières comme les mathématiques ou la lecture, la proportion des élèves ayant atteint un seuil de résultat de test minimal, etc. Lorsque vous exécutez l’outil Agrégation multivariée spatialement contrainte, une valeur R2 est calculée pour chaque variable et reportée dans la fenêtre de messages. Dans le récapitulatif ci-dessous, par exemple, les zones scolaires sont agrégées en fonction des résultats des tests des élèves, du pourcentage d’adultes dans la zone qui n’ont pas terminé leur scolarité, des dépenses par élève et du nombre moyen d’élèves par enseignant. Notez que la variable de résultats des tests TestScores présente la valeur R2 la plus élevée. Il s’agit donc de la variable qui divise le plus efficacement les zones scolaires en agrégats. La valeur R2 reflète dans quelle mesure la variation des données TestScores d'origine a été conservée après l’agrégation. Par conséquent, plus la valeur R2 est élevée pour une variable donnée, plus cette variable permet de mieux différencier les entités.
Approfondissement :
La valeur R2 se calcule de la façon suivante :
(TSS - ESS) / TSSoù SCT représente la somme des carrés totale et SCE, la somme des carrés expliquée. La somme des carrés totale se calcule en élevant au carré puis en additionnant les écarts par rapport à la valeur moyenne globale d’une variable. La somme des carrés expliquée se calcule de la même façon, hormis que les écarts sont considérés par groupe : chaque valeur est soustraite de la valeur moyenne pour le groupe auquel elle appartient, puis élevée au carré et additionnée.
Contraintes de taille d’agrégat
La taille d’agrégat peut être gérée à l'aide du paramètre Cluster Size Constraints (Contraintes de taille d’agrégat). Vous pouvez définir un seuil minimal et un seuil maximal que chaque agrégat doit satisfaire. Les contraintes de taille peuvent concerner soit le Number of Features (Nombre d'entités) que chaque agrégat doit contenir, soit la somme d’une Attribute Value (Valeur attributaire). Si, par exemple, vous agrégez des comtés des États-Unis sur la base de variables économiques, vous pouvez spécifier que chaque agrégat compte une population minimale de 5 millions et une population maximale de 25 millions d’habitants. Alternativement, vous pouvez spécifier que chaque agrégat doit contenir un minimum de 30 comtés.
Lorsqu’une contrainte Maximum per Cluster (Maximum par agrégat) est spécifiée, l’algorithme commence avec un seul agrégat et divise les agrégats spatialement contigus et similaires en valeur. De nouveaux agrégats sont créés jusqu’à ce que toutes les tailles d’agrégat soient inférieures à la valeur Maximum per Cluster (Maximum par agrégat), en tenant compte de la totalité des variables pour chaque division.
La méthode SKATER forme des agrégats en partitionnant spatialement les données ayant des valeurs similaires pour les entités d’intérêt. Il est possible que le paramètre Cluster Size Constraints (Contraintes de taille d’agrégat) ne soit pas respecté pour tous les agrégats. Ce peut être le cas si les contraintes de taille d’agrégat définies ne se prêtent pas à des définitions optimales d’agrégats.
La méthode SKATER forme également des agrégats en partitionnant spatialement les données ayant des valeurs similaires pour tous les Analysis Fields (Champs d’analyse) spécifiés. Il est possible que les Cluster Size Constraints (Contraintes de taille d’agrégat) ne soient pas respectées pour tous les agrégats. Ce peut être le cas si une contrainte maximale et une contrainte minimale ont été définies avec des valeurs proches, ou en raison de la façon dont l’arbre couvrant de poids minimal a été construit sur la base de contraintes spatiales. Le cas échéant, l’outil s’arrête et les agrégats non conformes aux spécifications requises sont signalés dans la fenêtre des messages.
Nombre d’agrégats
Vous connaîtrez parfois le nombre d’agrégats qui convient le mieux à votre question ou votre problème. Si vous avez cinq directeurs commerciaux et si vous voulez leur affecter leur propre région contiguë, par exemple, spécifiez 5 comme valeur du paramètre Number of Clusters (Nombre d’agrégats). Cependant, dans de nombreux cas, vous ne disposez d’aucun critère vous permettant de sélectionner un nombre spécifique d’agrégats, et vous voulez au contraire connaître le nombre qui vous permettra de distinguer le mieux possible les différences et les similarités entre les entités. Pour vous aider dans ce cas de figure, vous pouvez laisser le paramètre Number of Clusters (Nombre d’agrégats) non renseigné et laisser l’outil Agrégation multivariée spatialement contrainte évaluer l’efficacité de la division de vos entités en 2 à 30 agrégats. L’efficacité de l’agrégation se mesure à l’aide de la statistique pseudo-F de Calinski-Harabasz, qui est un ratio de la variance entre agrégats par rapport à la variance au sein d’un agrégat : En d’autres termes, il s’agit d’un ratio reflétant la similarité intragroupe et la différence intergroupe comme suit :

Supposons que vous voulez créer quatre agrégats spatialement contigus. Dans ce cas, l’outil crée un arbre couvrant de poids minimal qui représente à la fois la structure spatiale de vos entités et les valeurs de champ d’analyse qui leur sont associées. Puis, l’outil détermine le meilleur emplacement où scinder l’arbre en deux agrégats distincts. Il détermine ensuite lequel des deux agrégats obtenus doit être divisé afin d’obtenir la meilleure solution à trois agrégats. Un des deux agrégats est divisé, l’autre agrégat demeurant intact. Enfin, il détermine lequel des trois agrégats obtenus doit être divisé afin d’obtenir la meilleure solution à quatre agrégats. Pour chaque division, la meilleure solution est celle qui optimise à la fois la similarité à l’intérieur de l’agrégat et la différence entre les agrégats. Un agrégat ne peut plus être divisé (sauf arbitrairement) dès lors que les valeurs de champ d’analyse de toutes les entités de cet agrégat sont identiques. Dans le cas où tous les agrégats obtenus renferment des entités identiques, l’outil Agrégation multivariée spatialement contrainte cesse de créer d’autres agrégats, même s’il n’a pas encore atteint la valeur définie pour Number of Clusters (Nombre d’agrégats). Il n’y a pas lieu de diviser un agrégat lorsque tous les Analysis Fields (Champs d’analyse) ont des valeurs identiques.
Contraintes spatiales
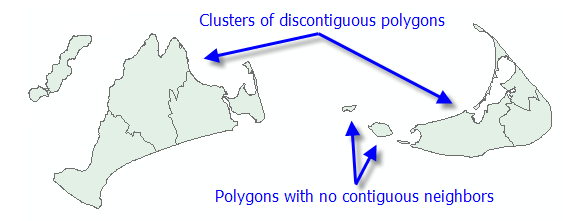
Le paramètre Spatial Constraints (Contraintes spatiales) garantit que les agrégats obtenus sont spatialement proches. Les options Contiguity (Contiguïté) sont activées pour les classes d'entités surfaciques et indiquent que les entités peuvent seulement faire partie du même agrégat si elles partagent une limite (Contiguity edges only (Tronçons de contiguïté uniquement)) ou si elles partagent soit une limite, soit un sommet (Contiguity edges corners (Angles des tronçons de contiguïté)) avec un autre membre de l’agrégat. Les options de contiguïté des polygones ne sont cependant pas appropriées si votre jeu de données inclut des agrégats de polygones non contigus ou de polygones sans aucun voisin contigu.
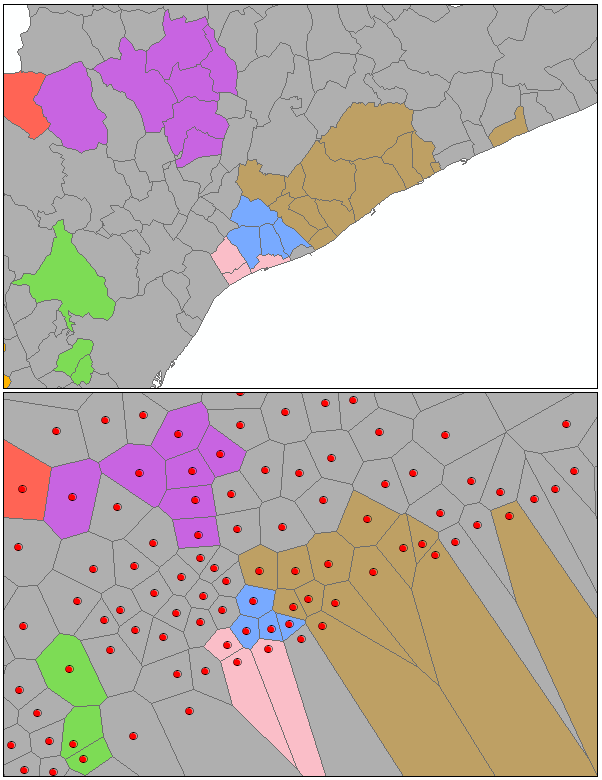
L’option Trimmed Delaunay triangulation (Triangulation de Delaunay avec élimination des points) convient aux entités surfaciques et ponctuelles et garantit qu’une entité fait partie d’un agrégat uniquement si au moins un autre membre de l’agrégat est un voisin naturel (Triangulation de Delaunay). En principe, la triangulation de Delaunay crée un maillage de triangles non superposés à partir de centroïdes d'entités. Chaque entité est un nœud de triangle, et les nœuds qui partagent des segments sont considérés comme voisins. Ces triangles sont ensuite découpés selon une enveloppe convexe de sorte que les entités ne puissent pas avoir pour voisines d’autres entités situées en dehors de l’enveloppe convexe. Cette option ne doit pas être utilisée pour les jeux de données contenant des entités coïncidentes. En outre, puisque la méthode de triangulation de Delaunay convertit les entités en polygones de Thiessen pour déterminer les relations de voisinage, particulièrement dans le cas des entités surfaciques et parfois des entités périphériques de votre jeu de données, les résultats obtenus avec cette option peuvent ne pas être ceux auxquels vous vous attendiez. Dans l’illustration ci-dessous, vous pouvez observer que certains polygones d’origine regroupés ne sont pas contigus. Cependant, une fois converties en polygones de Thiessen, toutes les entités regroupées partagent bien un segment.
Pour obtenir des agrégats spatialement et temporellement proches, créez un fichier de matrice de pondérations spatiales (SWM) à l’aide de l’outil Générer la matrice de pondérations spatiales et sélectionnez Space time window (Fenêtre spatio-temporelle) comme valeur du paramètre Conceptualization of Spatial Relationships (Conceptualisation de relations spatiales). Vous pouvez alors spécifier le fichier SWM que vous avez créé à l’aide de l’outil Générer la matrice de pondérations spatiales comme valeur du paramètre Weights Matrix File (Fichier de matrice de pondérations) lorsque vous exécutez l’outil Agrégation multivariée spatialement contrainte.
Remarque :
Alors que les relations spatiales entre les entités sont stockées dans un fichier SWM et utilisées par l’outil Agrégation multivariée spatialement contrainte pour imposer des contraintes spatiales, le processus d’agrégation n’implique en réalité aucune pondération. Le fichier SWM est uniquement utilisé pour vérifier quelles entités peuvent ou non être incluses dans le même agrégat.
Arbre couvrant de poids minimal
Pour limiter l’appartenance des agrégats aux entités contiguës ou proximales, l’outil construit d’abord un diagramme de connectivité représentant les relations de voisinage entre les entités. À partir du diagramme de connectivité, un arbre couvrant de poids minimal est créé afin d’y synthétiser les relations spatiales des entités et la similarité des données des entités. Les entités deviennent des nœuds de l’arbre couvrant de poids minimal, reliés par des segments pondérés. La pondération de chaque segment est proportionnelle à la similarité des objets qu’il connecte. Une fois l’arbre couvrant de poids minimal créé, une branche (un segment) de l’arbre est coupée, ce qui a pour effet de créer deux arbres couvrants de poids minimal. Le segment à couper est sélectionné de façon à minimiser les dissemblances dans les agrégats résultants, tout en évitant (si possible) les singletons (agrégats à une seule entité). À chaque itération, un des arbres couvrants de poids minimal est divisé par ce processus d’élagage jusqu’à ce que la valeur Number of Cluster (Nombre d’agrégats) définie soit atteinte. La méthode publiée employée s’appelle « SKATER » (pour Spatial «K »luster Analysis by Tree Edge Removal). Alors que la branche qui optimise la similarité des agrégats est sélectionnée pour élagage à chaque itération, il n'est pas possible de garantir un résultat final optimal.
Probabilités d’appartenance
Le paramètre Permutations to Calculate Membership Probabilities (Permutations pour calculer les probabilités d’appartenance) définit le nombre de permutations à effectuer pour le calcul de la probabilité d’appartenance des agrégats à l’aide de signes d’accumulation. Les probabilités d’appartenance sont incluses dans la classe d’entités en sortie dans le champ PROB. Une probabilité d’appartenance élevée indique que l’entité partage des similitudes et une proximité avec l’agrégat auquel elle est affectée, ce qui vient confirmer que l’entité appartient à l’agrégat auquel elle est assignée. Une faible probabilité peut indiquer que l’entité est très différente de l’agrégat auquel elle a été affectée par l’algorithme SKATER ou qu’elle pourrait faire partie d’un autre agrégat dans le cas d’une modification particulière des paramètres Analysis Fields (Champs d’analyse), Cluster Size Constraints (Contraintes de taille d’agrégat) ou Spatial Constraints (Contraintes spatiales).
Le nombre de permutations spécifié détermine le nombre d’arbres couvrant de poids minimal aléatoire à créer pour perturber la contrainte spatiale de l’algorithme SKATER. L’algorithme résout ensuite le Number of Clusters (Nombre d’agrégats) spécifié pour chaque arbre couvrant de poids minimal aléatoire. En utilisant les agrégats d’origine définis par SKATER, le processus de permutation suit la fréquence à laquelle les membres d’un agrégat sont agrégés ensemble sous les arbres couvrant de poids minimal changeants. Les entités ayant tendance à changer d’agrégat, à la suite de légères modifications apportées à l’arbre couvrant de poids optimal, obtiennent de faibles probabilités d’appartenance tandis que les entités qui ne changent pas d’agrégat obtiennent de fortes probabilités d’appartenance.
Le calcul de ces probabilités peut prendre beaucoup de temps pour les jeux de données volumineux. Il est recommandé de commencer par exécuter plusieurs itérations pour trouver le nombre optimal d’agrégats pour votre analyse et, dans un deuxième temps, de calculer les probabilités pour votre analyse. Vous pouvez également accroître les performances en réglant le paramètre Parallel Processing Factor (Facteur de traitement parallèle) sur 50.
Sorties
L’outil Agrégation multivariée spatialement contrainte produit plusieurs sorties. Vous pouvez accéder aux messages depuis la fenêtre Geoprocessing (Géotraitement) en pointant sur la barre de progression, en cliquant sur le bouton de progression de l’outil  ou en développant la section des messages au bas de la fenêtre Geoprocessing (Géotraitement). Vous pouvez également accéder aux messages d'une précédente exécution de l'outil Agrégation multivariée spatialement contrainte via l'historique de géotraitement.
ou en développant la section des messages au bas de la fenêtre Geoprocessing (Géotraitement). Vous pouvez également accéder aux messages d'une précédente exécution de l'outil Agrégation multivariée spatialement contrainte via l'historique de géotraitement.
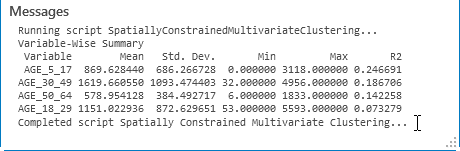
La sortie par défaut de l’outil Agrégation multivariée spatialement contrainte est une nouvelle classe d’entités en sortie contenant les champs utilisés dans l’analyse ainsi qu’un nouveau champ d’entier appelé CLUSTER_ID permettant d’identifier à quel groupe appartient chaque entité. Cette classe d’entités en sortie est ajoutée à la table des matières et un rendu unique de combinaison de couleurs est appliqué au champ CLUSTER_ID.
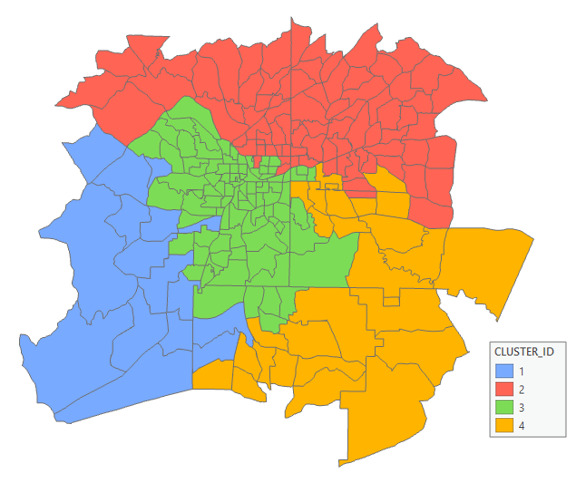
Sorties de diagramme d’agrégation multivariée spatialement contrainte
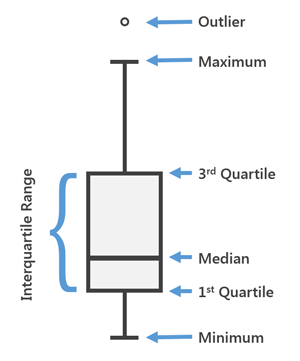
Des diagrammes de types divers sont créés pour récapituler les agrégats ayant été créés. Les boîtes à moustaches permettent d’afficher les informations concernant les caractéristiques de chaque agrégat et de chaque variable utilisée dans l’analyse. Le diagramme ci-dessous montre comment interpréter les boîtes à moustaches et leurs valeurs récapitulatives pour chaque Analysis Field (Champ d’analyse) et chaque agrégat créé : valeur minimale des données, 1er quartile, moyenne globale, 3e quartile, valeur maximale des données et points aberrants des données (valeurs inférieures ou supérieures à 1,5 fois l’écart interquartile). Positionnez le pointeur sur la boîte à moustaches pour visualiser ces valeurs ainsi que la valeur d’écart interquartile. Toutes les marques de points situées au-delà du minimum ou du maximum (moustache supérieure ou inférieure) représentent des points de données aberrants.
Approfondissement :
L’écart interquartile (IQR) correspond à la différence entre le 3e quartile et le 1er quartile. Les points aberrants faibles sont des valeurs inférieures à 1,5*IQR (Q1-1,5*IQR), et les points aberrants élevés sont des valeurs supérieures à 1,5*IQR (Q3+1,5*IQR). Les points aberrants apparaissent sous forme de symboles ponctuels dans les boîtes à moustaches.
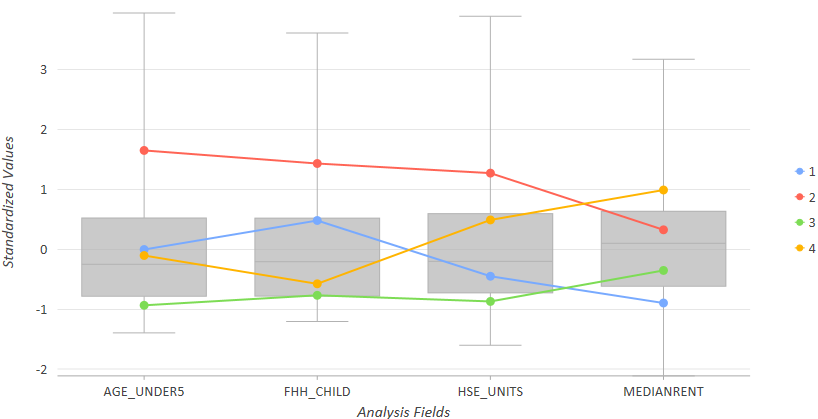
Le diagramme de boîte à moustaches parallèle par défaut récapitule les agrégats et les variables qu’ils contiennent. Par exemple, l’outil Agrégation multivariée spatialement contrainte a été exécuté sur des secteurs de recensement pour créer quatre agrégats. Dans le diagramme ci-dessous, notez que l’agrégat 2 (en rouge) représente les secteurs avec des loyers à peu près moyens, le plus grand nombre de foyers avec des enfants dont le chef de famille est une femme (FHH_CHILD), le plus grand nombre de logements (HSE_UNITS) et le plus grand nombre d’enfants de moins de 5 ans. L’agrégat 2 (mordoré) représente les secteurs dont les loyers moyens sont les plus élevés, la proportion presque la plus faible de foyers avec enfants dont le chef de famille est une femme et un nombre de logements plus élevé que la moyenne. L’agrégat 3 (en vert) représente les secteurs ayant la proportion la plus basse de foyers avec enfants dont le chef de famille est une femme, la proportion la plus faible d’enfants sous l’âge de 5 ans, le plus faible nombre de logements et les loyers presque les plus bas (pas aussi bas que ceux de l’agrégat 1). Positionnez le pointeur sur chaque nœud des lignes de moyenne pour visualiser la valeur moyenne de l’agrégat pour chaque Analysis Field (Champ d’analyse).
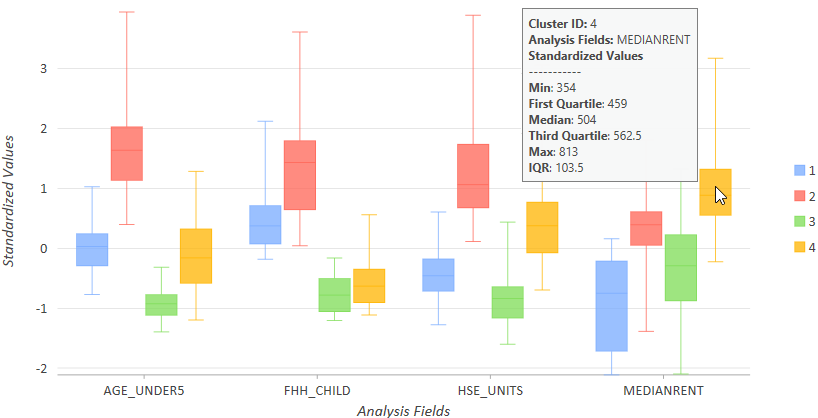
Après inspection du récapitulatif global de l’analyse avec les boîtes à moustaches parallèles ci-dessus, vous pouvez examiner les boîtes à moustaches de chaque agrégat pour chaque variable en sélectionnant Side-by-side (Côte à côte) dans l’onglet Series (Série) de la fenêtre Chart Properties (Propriétés du diagramme). Cette vue des données vous permet de repérer le groupe qui présente la plage de valeurs la plus élevée et la plus basse pour chaque variable. Les boîtes à moustaches sont créées pour chaque agrégat pour chaque variable, si bien que vous pouvez voir le type de relation des valeurs de chaque agrégat avec les autres agrégats créés. Positionnez le pointeur sur la boîte à moustaches de chaque variable pour afficher les valeurs minimale, maximale et médiane pour chaque variable de chaque agrégat. Dans l’exemple du diagramme ci-dessous, on peut voir que l’agrégat 4 (en or) présente les valeurs les plus élevées pour la variable MEDIANRENT et englobe des secteurs dont la plage de valeurs est comprise entre 354 et 813.
Un diagramme à barres, indiquant le nombre d’entités par agrégat, est également créé. En sélectionnant chaque diagramme, on sélectionne également les entités de cet agrégat sur la carte, ce qui peut s’avérer utile pour une analyse supplémentaire.
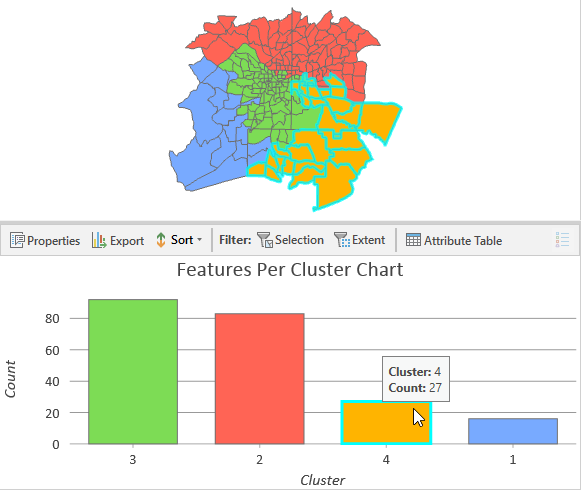
Lorsque vous laissez le paramètre Number of Clusters (Nombre d’agrégats) non renseigné, l’outil évalue le nombre optimal d’agrégats en fonction de vos données. Lorsque vous spécifiez un chemin d’accès à la Output Table for Evaluating Number Clusters (Table de sortie pour l’évaluation du nombre d’agrégats), un diagramme affichant les valeurs de statistique pseudo-F calculées est créé. Le pic le plus haut sur le diagramme représente la statistique F la plus élevée, correspondant au nombre d’agrégats qui permet de distinguer le mieux les entités et les variables spécifiées. Dans le diagramme ci-dessous, la statistique F associée à quatre groupes est la plus élevée. Cinq groupes, avec une statistique pseudo-F élevée, conviendraient également.

Meilleures pratiques
Alors que l’on a tendance à vouloir inclure autant de Analysis Fields (Champs d’analyse) que possible, dans le cas de cet outil Agrégation multivariée spatialement contrainte, il vaut mieux commencer avec une seule variable puis en ajouter. Les résultats sont plus faciles à interpréter avec moins de champs d’analyse. Il est également plus simple de déterminer quelles variables sont les meilleurs discriminants lorsque les champs sont peu nombreux.
Dans de nombreux cas, vous exécuterez plusieurs fois l’outil Agrégation multivariée spatialement contrainte avant de rechercher le Number of Clusters (Nombre d’agrégats) optimal, les Spatial Constraints (Contraintes spatiales) les plus efficaces, ainsi que la combinaison de Analysis Fields (Champs d’analyse) permettant de diviser au mieux vos entités en agrégats.
Si l’outil indique que le nombre optimal d’agrégats est 30, veillez à examiner le diagramme des statistiques F. Le choix du nombre d’agrégats et l’interprétation du diagramme de statistique F est assez subtil, et un nombre d’agrégats moins élevé peut s’avérer plus approprié pour votre analyse.
Ressources supplémentaires
Duque, J. C., R. Ramos, and J. Surinach. 2007. "Supervised Regionalization Methods: A Survey" dans International Regional Science Review 30: 195–220.
Assuncao, R. M., M. C. Neves, G. Camara, and C. Da Costa Freitas. 2006. "Efficient Regionalisation Techniques for Socio-economic Geographical Units using Minimum Spanning Trees" dans International Journal of Geographical Information Science 20 (7): 797–811.
Vous avez un commentaire à formuler concernant cette rubrique ?