Fonctionnement de l’outil Relations bivariées locales

Un composant important de nombreux processus d’analyse SIG est la comparaison de deux variables dans une zone d’étude en vue de déterminer si ces variables sont liées et comment elles sont liées. Par exemple, existe-t-il une relation entre le diabète et l’obésité dans certaines régions ? Historiquement, la comparaison cartographique ou l’analyse de régression linéaire a permis de répondre à ces types de questions. La comparaison cartographique peut être subjective et l’analyse de régression permet uniquement de détecter les relations simples.

L’outil Relations bivariées locales permet de quantifier la relation entre deux variables sur la même carte en déterminant si les valeurs d’une variable dépendent de ou sont influencées par les valeurs d’une autre variable et si ces relations évoluent dans l’espace géographique. L'outil calcule une entropie statistique dans chaque voisinage local, qui quantifie la quantité d’informations partagées entre les deux variables. Contrairement à d’autres statistiques qui peuvent uniquement capturer les relations linéaires (la régression linéaire, par exemple), l’entropie peut capturer n’importe quelle relation structurelle entre les deux variables, notamment les relations exponentielles, quadratiques, sinusoïdales et même complexes qui ne peuvent pas être représentées par les fonctions mathématiques classiques. Cet outil accepte les polygones ou les points et génère une classe d’entités en sortie qui récapitule la signification et la forme des relations de chaque entité en entrée. En outre, des fenêtres contextuelles personnalisées et différents diagnostics, diagrammes et messages sont fournis.

Applications possibles

L’outil peut s’utiliser dans les types d’application suivants :

• Le CDC (Centers for Disease Control and Prevention) indique : « Les personnes souffrant d’obésité, par rapport aux personnes dont le poids est normal ou idéal, présentent un risque plus élevé de contracter des maladies ou affections graves, notamment le diabète de type 2. » Le CDC pourrait utiliser cet outil pour quantifier l’intensité de la relation entre l’obésité et le diabète et déterminer si la relation est cohérente dans toute la zone d’étude.
• Un responsable de la santé publique pourrait explorer les relations entre les niveaux de pollution de l’air et les facteurs socioéconomiques pour révéler une éventuelle injustice environnementale.

Méthode d’entropie

Qu’est-ce que cela signifie, pour deux variables, d’être associées ? Il existe de nombreux types de relations entre variables, mais au sens le plus simple, deux variables sont associées si des informations concernant une variable peuvent être obtenues par l’observation des valeurs de l’autre variable. Par exemple, vous pouvez obtenir des informations sur le risque de diabète en observant les informations sur l’obésité. Ceci s’appelle la dépendance entre deux variables. À l’inverse, si l’observation d’une variable ne permet pas d’obtenir des informations sur l’autre variable, les variables sont dites indépendantes.

L’entropie permet de mesurer le degré de relation entre des variables. C’est un concept fondamental de la théorie de l’information, qui permet de quantifier le niveau d’incertitude dans une variable aléatoire. En règle générale, moins la variable est prévisible et plus l’entropie est élevée. L’entropie peut s’appliquer de manière large et être calculée pour chaque variable aléatoire. Il est également possible de calculer une entropie conjointe entre deux variables ou plus. L’entropie conjointe de deux variables est égale à l’entropie de la première variable plus l’entropie de la seconde variable, moins les informations mutuelles des deux variables. Les informations mutuelles sont utiles pour connaître le niveau de dépendance entre les variables, car elles mesurent directement la quantité d’informations qui peut être obtenue au sujet d’une variable par l’observation des valeurs de l’autre variable.

Afin d’estimer les informations mutuelles, l’entropie de chaque variable et son entropie conjointe doivent être estimées. Ces valeurs dépendent toutefois des distributions sous-jacentes des variables et ne sont presque jamais connues dans la pratique. Heureusement, une recherche récente a montré que l’entropie conjointe de plusieurs variables peut être estimée en utilisant les arbres couvrants de poids minimal avec puissance pondérée à la place de la distribution conjointe des variables (Guo, 2010). Ceci permet d’estimer l’entropie conjointe sans connaître les distributions individuelles des deux variables. Il est utile de pouvoir estimer l’entropie conjointe, mais il vous faut vraiment connaître les informations mutuelles entre les deux variables en vue de déterminer si ces variables sont associées. Même s’il n’est pas possible d’estimer directement les informations mutuelles sans connaître les distributions des deux variables, il est possible d’utiliser les permutations afin d’élaborer un test d’hypothèse nulle pour les relations statistiquement significatives.

Test des relations significatives à l’aide des permutations

Comme expliqué dans la section précédente, la question de savoir si deux variables sont associées revient à se demander si leur entropie conjointe (qui peut être estimée) est de beaucoup inférieure à la somme des entropies individuelles des deux variables (qui ne peuvent pas être estimées). Pour le dire différemment, l’entropie conjointe estimée des données est-elle de beaucoup inférieure à ce qu’elle serait si les deux variables étaient indépendantes ?

Pour le savoir, des permutations sont appliquées aux variables en réattribuant de manière aléatoire chaque valeur de la première variable sur une nouvelle valeur de la seconde variable. En rendant les appariements aléatoires, les jeux de données permutés ne partagent aucune information mutuelle, mais les entropies individuelles des deux variables ne changent pas. En générant de nombreux jeux de données permutés et en estimant l’entropie conjointe de chacun d’entre eux, il est possible de construire une distribution de l’entropie conjointe sous l’hypothèse nulle selon laquelle les deux variables sont indépendantes et non associées. L’entropie conjointe estimée à partir des données réelles peut ensuite être comparée à cette distribution, et une pseudo valeur p peut être calculée en fonction de la proportion des permutations dont l’entropie conjointe est inférieure à l’entropie conjointe des données réelles.

Test des relations spatiales locales

La procédure décrite ci-dessus, qui permet de tester les relations significatives entre deux variables, peut s’appliquer à toutes les données bivariées continues. Pour la transformer en test des relations spatiales locales, ce test d’hypothèse nulle est réalisé sur chaque entité en entrée à l’aide des voisinages. Ceci vous permet de représenter les résultats et d’identifier les zones locales où les variables ont une relation significative.

Toutes les valeurs des paramètres Dependent Variable (Variable dépendante) et Explanatory Variable (Variable explicative) sont d’abord redimensionnées pour être comprises entre 0 et 1 en soustrayant la valeur minimale du jeu de données entier et en divisant le résultat par la plage (maximum moins minimum) du jeu de données entier. La procédure suivante est ensuite réalisée pour chaque entité en entrée :

1. Recherchez les entités voisines les plus proches. Le paramètre Number of Neighbors (Nombre de voisins) indique le nombre de voisins à utiliser. L’entité en entrée est comptabilisée comme voisine d’elle-même.
2. Combinez les valeurs des deux variables redimensionnées issues des voisins dans un jeu de données unique.
3. Construisez l’arbre couvrant de poids minimal et estimez l’entropie conjointe.
4. Permutez de façon aléatoire les valeurs des deux variables et estimez l’entropie conjointe de chaque permutation. Le paramètre Number of Permutations (Nombre de permutations) indique le nombre de permutations à effectuer.
5. Calculez la pseudo valeur p et déterminez si les variables ont une relation statistiquement significative.

Comme cette procédure réalise un test d’hypothèse nulle différent sur chaque entité en entrée, vous pouvez utiliser le paramètre Apply False Discovery Rate (FDR) Correction (Appliquer la correction FDR [False Discovery Rate]) pour contrôler la proportion de faux positifs (erreurs de type 1).

Classifier les relations locales

Il est très important d’identifier les zones dans lesquelles deux variables ont une relation statistiquement significative. Pour mettre à profit ces informations, il est utile d’identifier le type de relation existant entre les variables en fonction du degré de fiabilité avec lequel la variable explicative peut prévoir la variable dépendante.

Chaque entité est classée dans un des types de relations suivants :

• Not Significant (Non significatif) : la relation entre les variables n’est pas statistiquement significative.
• Positive Linear (Linéaire positif) : la variable dépendante augmente de façon linéaire à mesure que la variable explicative augmente.
• Negative Linear (Linéaire négatif) : la variable dépendante diminue de façon linéaire à mesure que la variable explicative augmente.
• Concave : la variable dépendante change selon une courbe concave à mesure que la variable explicative augmente. En règle générale, les courbes concaves sont dirigées vers le bas.
• Convex (Convexe) : la variable dépendante change selon une courbe convexe à mesure que la variable explicative augmente. En règle général, les courbes convexes sont dirigées vers le haut.
• Undefined complex (Complexe indéfini) : les variables sont significativement liées, mais le type de relation ne peut pas être décrit de manière fiable par les autres catégories.

Les images suivantes sont des exemples d’une relation de type Concave :

Des exemples typiques de relations concaves entre deux variables sont présentés.

Les images suivantes sont des exemples d’une relation de type Convex (Convexe) :

Des exemples typiques de relations convexes entre deux variables sont présentés.

Classez chaque entité significative en procédant comme suit :

1. Estimez un modèle de régression linéaire ordinaire pour prévoir la variable dépendante en fonction de la variable explicative et calculez le critère d’information d’Akaike (AICc) du modèle.
2. Estimez un second modèle de régression linéaire pour prévoir la variable dépendante en fonction de la variable explicative et du carré de la variable explicative (modèle de régression quadratique) et calculez le critère d’information d’Akaike (AICc).
3. Comparez les valeurs AICc des deux modèles de régression et choisissez celle qui représente le mieux la relation. La valeur AICc du modèle de régression quadratique doit être inférieure d’au moins 3 points à la valeur AICc du modèle de régression linéaire pour que le modèle quadratique soit retenu. Sinon, c’est le modèle linéaire qui est choisi.
4. Pour le modèle choisi, calculez la valeur R² ajustée. Si elle est inférieure à 0,05, le modèle choisi explique moins de 5 pour cent de la variation des données et la relation est classée comme étant de type Undefined Complex (Complexe non définie).
5. Si la valeur R² ajustée est supérieure à 0,05, effectuez la classification selon les règles suivantes :
   • Si un modèle linéaire est choisi et que le coefficient est positif, la classification est de type Positive Linear (Linéaire positive).
   • Si le modèle linéaire est choisi et que le coefficient est négatif, la classification est de type Negative Linear (Linéaire négative).
   • Si le modèle quadratique est choisi et que le coefficient de l’expression au carré est positif, la classification est de type Convex (Convexe).
   • Si le modèle quadratique est choisi et que le coefficient de l’expression au carré est négatif, la classification est de type Concave.

Interpréter les résultats

La sortie de cet outil est une classe d’entités symbolisée par le type de relation, ainsi que des statistiques imprimées dans des messages de géotraitement. Les entités en sortie contiennent des champs d’informations et des fenêtres contextuelles qui visualisent la relation à l’aide de nuages de points.

Fenêtres contextuelles en nuages de points

Si cela est spécifié, des fenêtres contextuelles en nuages de points sont générées pour chaque entité en sortie. Pour les afficher, il suffit de cliquer sur l’entité dans la carte. L’image suivante montre une fenêtre contextuelle en nuages de points avec une relation linéaire positive :

Une fenêtre contextuelle en nuages de points pour une relation linéaire positive est illustrée.

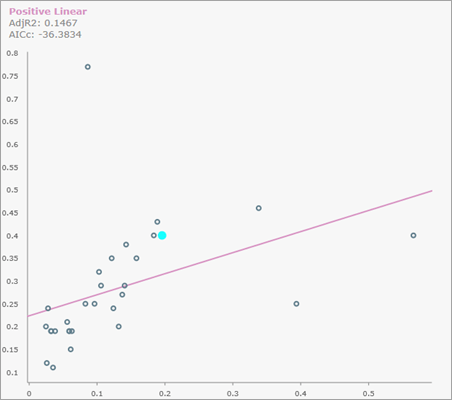
La variable explicative redimensionnée s’affiche sur l’axe x et la variable dépendante redimensionnée sur l’axe y. L’unique point en surbrillance dans le nuage de points représente l’entité ; tous les autres points sont les voisins de l’entité.

Survolez un point dans le nuage de points pour voir la valeur du paramètre Source ID (ID source) de l’entité et examiner les valeurs redimensionnées des variables dépendante et explicative ainsi que leur valeur brute (échelle d’origine) entre parenthèses.

Messages de géotraitement

Des informations récapitulatives sur la signification statistique et les types de relations apparaissent sous la forme de messages de géotraitement. Vous en trouverez ci-dessous un exemple de ces messages :

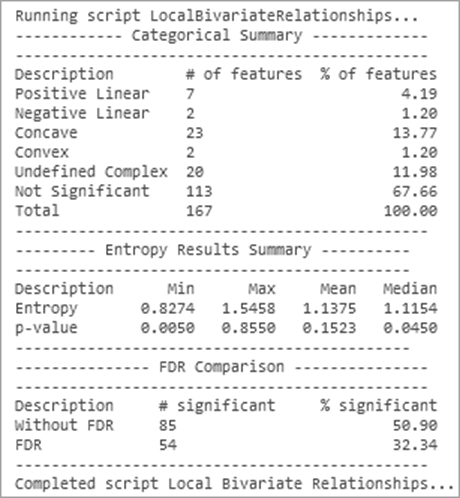
La section Categorical Summary (Résumé catégoriel) du message répertorie le nombre d’entités et les pourcentages pour chaque type de relation. La section Entropy Results Summary (Résumé des résultats d’entropie) indique le minimum (Min), le maximum (Max), la moyenne (Moyenne) et la médiane (Médiane) de l’entropie et les valeurs p des entités en entrée. La section FDR Comparison (Comparaison FDR) indique le nombre et le pourcentage de relations ayant une signification statistique avec et sans l’application d’une correction FDR (False Discovery Rate).

Remarque :

Les messages de géotraitement apparaissent au bas de la fenêtre Geoprocessing (Géotraitement) au cours de l’exécution de l’outil. Vous pouvez également accéder aux messages via l’historique de géotraitement en survolant la barre de progression, en cliquant sur le bouton contextuel ou en développant la section des messages dans la fenêtre Geoprocessing (Géotraitement).

Champs en sortie

La sortie de l’outil contient divers champs qui fournissent des informations indiquant comment et pourquoi chaque entité a été catégorisée dans son type de relation.

Signification de la relation

Les champs suivants fournissent des informations indiquant si la relation entre les variables dépendante et explicative ont une signification statistique ou non :

• Entropy : la valeur d’entropie estimée de l’entité.
• P-values : la pseudo valeur p du test pour une relation significative entre les variables dépendante et explicative. Cette valeur n’est pas ajustée pour la correction FDR (False Discovery Rate).
• Local Bivariate Relationship Confidence Level : le niveau le plus élevé de confiance atteint pour l’entité. Les valeurs possibles de ce champ sont 90% Confident (Confiance à 90 %), 95% Confident (Confiance à 95 %), 99% Confident (Confiance à 99 %) et Not Significant (Non significatif). Le niveau de confiance s’ajuste à la correction FDR (False Discovery Rate) si un paramètre Apply False Discovery Rate (FDR) Correction (Appliquer la correction FDR (False Discovery Rate)) est spécifié.

Classification des relations

Les champs suivants fournissent des informations sur la classification du type de relation entre les variables dépendante et explicative :

• Type of Relationship : le type de relation entre les variables dépendante et explicative
• AICc (Linear) : le critère d’information Akaike corrigé pour le modèle linéaire
• R-squared (Linear) : la valeur R² du modèle linéaire
• AICc (Polynomial) : le critère d’information Akaike corrigé pour le modèle polynomial
• R-squared (Polynomial) : la valeur R² du modèle polynomial

Remarque :

Les valeurs AICc et R² sont nulles pour les entités n’ayant pas de relation statistiquement significative entre les variables dépendante et explicative.

Coefficients et signification de la régression

Les champs suivants fournissent des informations sur les coefficients des modèles linéaires et polynomiaux utilisés pour classer la relation :

• Intercept : l’intersection du modèle linéaire
• Coefficient (Linear) : le coefficient du terme linéaire du modèle linéaire
• Polynomial Intercept : l’intersection du modèle polynomial
• Polynomial Coefficient (Linear) : le coefficient du terme linéaire du modèle polynomial
• Polynomial Intercept (Squared) : le coefficient du terme au carré du modèle polynomial
• Significance of Coefficients (Linear) : un code à deux caractères indiquant si l’intersection et le coefficient ont une signification statistique à un niveau de confiance de 90 pour cent. Un trait de soulignement (_) indique que la valeur n’a pas de signification statistique et un astérisque (*) qu’elle en a une. Par exemple, *_ indique que l’intersection a une signification statistique mais pas le coefficient linéaire. De même, _* indique que l’intersection n’a pas de signification statistique mais que le coefficient linéaire en a une.
• Significance of Coefficients (Polynomial) : un code à trois caractères indiquant si l’intersection, le coefficient linéaire et le coefficient au carré du modèle polynomial ont une signification statistique à un niveau de confiance de 90 pour cent. Par exemple, *_* indique que l’intersection a une signification statistique, que le coefficient linéaire n’a pas de signification statistique et que le coefficient au carré a une signification statistique.

Remarque :

Tous les champs liés à des coefficients de régression sont nuls ou sont des chaînes vides pour chaque entité n’ayant pas de relation statistiquement significative entre les variables dépendante et explicative.

Astuces

Examinez les conseils suivants lorsque vous utilisez l’outil Relations bivariées locales :

• Utilisez le paramètre Scaling Factor (Facteur d’échelle) pour contrôler la sensibilité de l’outil par rapport à la subtilité des relations. Les facteurs d’échelle proches de zéro ne détectent que les relations fortes entre les variables. Les facteurs d’échelle proches de un peuvent, quant à eux, détecter en outre les relations les plus faibles. La valeur par défaut de 0,5 constitue un compromis qui détecte les relations fortes et modérées.
• La valeur que vous choisissez pour le paramètre Number of Neighbors (Nombre de voisins) a plusieurs implications importantes. L’utilisation d’un grand nombre de voisins fournit davantage de données pour chaque test d’hypothèse, ce qui augmente la probabilité de détecter une relation significative. Toutefois, l’utilisation de nombreux voisins a pour effet de délocaliser le test étant donné qu’il doit rechercher des voisins dans un voisinage plus lointain ; il peut ainsi ne pas parvenir à détecter des relations véritablement locales. Un grand nombre de voisins allonge également rapidement le délai d’exécution de l’outil.
• La valeur que vous choisissez pour le paramètre Number of Permutations (Nombre de permutations) est un compromis entre précision et augmentation du temps de traitement. L'augmentation du nombre de permutations améliore la précision en augmentant la plage des valeurs possibles pour la pseudo valeur de p. Ainsi, avec 99 permutations, la précision de la pseudo valeur de p est de 0,01, et pour 999 permutations, la précision est de 0,001. Ces valeurs sont calculées en divisant 1 par le nombre de permutations plus 1 : 1/(1+99) et 1/(1+999). Il est possible d’utiliser un nombre moins élevé de permutations lors de la première exploration d’un problème, mais il est recommandé d’augmenter les permutations jusqu’au nombre le plus élevé possible pour les résultats finaux. Il est également recommandé d’utiliser un grand nombre de permutations lorsque vous utilisez un grand nombre de voisins.

Référence

• Guo, D. "Local entropy map: a nonparametric approach to detecting spatially varying multivariate relationships." International Journal of Geographical Information Science 24, no. 9 (septembre 2010): 1367-1389.