Disponible avec une licence Spatial Analyst.
Disponible avec une licence 3D Analyst.
L’outil Pente identifie la déclivité de chaque cellule de la surface raster. Plus la valeur de la pente est faible, plus le terrain est plat ; plus la valeur de la pente est élevée, plus le terrain est pentu.
Remarque :
L’outil Paramètres de surface offre une implémentation plus récente de la pente et est recommandé à la place de l’outil Pente. L’outil Pente ajuste un plan aux neuf cellules locales, mais un plan peut ne pas être un bon descripteur de paysage et est susceptible de masquer ou d’exagérer les variations naturelles qui vous intéressent. L’outil Paramètres de surface ajuste une surface au voisinage des cellules et non un plan, l’ajustement au terrain étant alors plus naturel.
L’outil Pente utilise une fenêtre de cellules de 3 par 3 pour calculer la valeur, tandis que l’outil Paramètres de surface autorise des tailles de fenêtre allant de 3 cellules par 3 à 15 cellules par 15. Les tailles de fenêtre plus grandes sont utiles avec des données d’élévation haute résolution pour capturer les traitements de surface au sol à une échelle appropriée. L’outil Paramètres de surface offre également une option de fenêtre adaptative qui évalue la variabilité locale du terrain et identifie la taille de voisinage appropriée la plus grande pour chaque cellule. Cela peut s’avérer utile dans le cas d’un terrain graduellement homogène interrompu par des cours d’eau, des routes ou des ruptures nettes de la pente.
Vous pouvez continuer à utiliser l’approche traditionnelle de l’outil Pente si vos résultats doivent correspondre exactement aux exécutions précédentes de l’outil ou si une exécution plus rapide est plus importante qu’un meilleur algorithme.
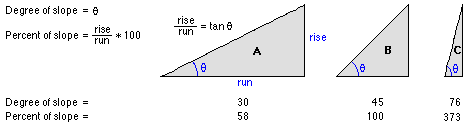
Le raster de pente en sortie peut être calculé dans deux types d'unités : degrés ou pourcentage (pourcentage d'élévation). Le pourcentage d'élévation peut être mieux compris si vous le considérez comme la hauteur calculée divisée par le parcours, multipliée par 100. Consultez le triangle B B ci-dessous. Lorsque l'angle est de 45 degrés, la hauteur calculée est égale au parcours et le pourcentage d'élévation est de 100 pour cent. Lorsque l'angle de pente se rapproche de la verticale (90 degrés), comme dans le triangle C, le pourcentage d'élévation se rapproche de l'infini.
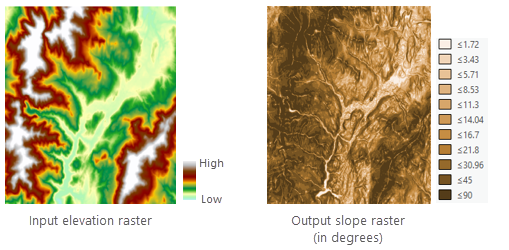
L'outil Pente est généralement appliqué à un jeu de données d'altitude, comme le montrent les images ci-dessous. Les pentes les plus raides apparaissent sur le raster de pente en sortie sous forme de couleur marron foncé ombré.
L'outil peut également être utilisé avec d'autres types de données continues, telles que des données de population, afin d'identifier d'importantes variations de valeur.
Méthodes de calcul et effet de limite
Il existe deux méthodes pour calculer la pente. Vous avez la possibilité d'effectuer des calculs Planar (Planaires) ou Geodesic (Géodésiques) avec le paramètre Method (Méthode).
Pour la méthode planaire, la pente est mesurée comme étant le taux de variation maximal des valeurs d'une cellule par rapport à ses voisines immédiates. Le calcul est effectué sur un plan plat projeté à l'aide d'un système de coordonnées cartésien 2D. La valeur de la pente est calculée à l’aide d’une estimation des différences finies de troisième ordre.
Avec la méthode géodésique, le calcul sera effectué dans un système de coordonnées cartésien 3D en considérant la forme de la Terre comme un ellipsoïde. La valeur de pente est calculée en mesurant l'angle entre la surface topographique et le point de référence.
Les calculs planaires et géodésiques sont réalisés à l'aide d'une cellule voisine de 3 x 3 (fenêtre mobile). Pour chaque voisinage immédiat, si la cellule centrale a une valeur NoData, la valeur en sortie est NoData. Le calcul nécessite également qu'au moins sept cellules voisines de la cellule de traitement aient des valeurs valides. Si le nombre de cellules valides est inférieur à sept, le calcul ne sera pas réalisé et la sortie à cette cellule de traitement sera égale à NoData.
Les cellules dans les lignes et colonnes les plus éloignées du raster en sortie seront égales à NoData. Cela s'explique par le fait que le long de la limite du jeu de données en entrée, ces cellules n'ont pas assez de voisins valides.
Méthode planaire
La pente est calculée comme le taux de variation (delta) de la surface dans les directions horizontale (dz/dx) et verticale (dz/dy) à partir de la cellule centrale vers chaque cellule adjacente. L'algorithme de base utilisé pour calculer la pente est le suivant :
slope_radians = ATAN ( √ ([dz/dx]2 + [dz/dy]2) )La pente est généralement mesurée en degrés, comme dans l'algorithme suivant :
slope_degrees = ATAN ( √ ([dz/dx]2 + [dz/dy]2) ) * 57.29578Remarque :
La valeur 57,29578 indiquée ici est une version tronquée du résultat de 180/pi.
L'algorithme de pente peut aussi être interprété comme suit :
slope_degrees = ATAN (rise_run) * 57.29578- où :
rise_run = √ ([dz/dx]2 + [dz/dy]2]
Les valeurs de la cellule centrale et de ses huit voisines déterminent les deltas horizontaux et verticaux. Les voisines sont identifiées par les lettres a à i, e représentant la cellule pour laquelle l'aspect est calculé.
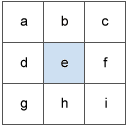
Le taux de variation dans la direction x pour la cellule e est calculé avec l'algorithme suivant :
[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize)- où :
wght1 et wght2 sont les nombres pondérés horizontaux des cellules valides.
Par exemple, si :
- c, f, eti ont tous des valeurs valides, wght1 = (1+2*1+1) = 4.
- i est égal à NoData, wght1 = (1+2*1+0) = 3.
- i est égal à NoData, wght1 = (1+2*0+1) = 2.
La même logique s'applique à wght2, mais les emplacements voisins sont a, d et g.
Le taux de variation dans la direction y pour la cellule e est calculé avec l'algorithme suivant :
[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4) / (8 * y_cellsize)- où :
wght3 et wght4 suivent le même concept que dans le calcul [dz/dx].
Exemple de calcul de pente planaire
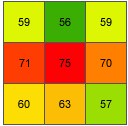
Dans cet exemple, la valeur de pente de la cellule centrale de la fenêtre mobile présentée ci-dessous sera calculée.
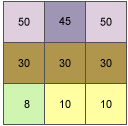
Le taux de variation dans la direction x pour la cellule centrale e est :
[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize) = ((50 + 60 + 10)*4/(1+2+1) - (50 + 60 + 8)*4/(1+2+1)) / (8 * 5) = (120 - 118) / 40 = 0.05Le taux de variation dans la direction y pour la cellule e est :
[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4) / (8 * y_cellsize) = ((8 + 20 + 10)*4/(1+2+1) - (50 + 90 + 50)*4/(1+2+1)) / (8 * 5) = (38 - 190 ) / 40 = -3.8En se basant sur le taux de variation dans les directions x et y, la pente de la cellule centrale e est calculée comme suit :
rise_run = √ ([dz/dx]2 + [dz/dy]2) = √ ((0.05)2 + (-3.8)2) = √ (0.0025 + 14.44) = 3.80032slope_degrees = ATAN (rise_run) * 57.29578 = ATAN (3.80032) * 57.29578 = 1.31349 * 57.29578 = 75.25762La valeur entière de la pente de la cellule e est 75 degrés.
Méthode géodésique
La méthode géodésique mesure la pente dans un système de coordonnées 3D géocentriques — également appelé système de coordonnées géocentriques à axes fixes (ECEF), — en considérant la forme de la Terre comme un ellipsoïde. Le résultat de calcul ne sera pas affecté par la façon dont le jeu de données est projeté. Il utilisera les unités z du raster en entrée s'ils sont définis dans la référence spatiale. Si la référence spatiale de l’entrée ne définit pas les unités z, vous devez le faire avec le paramètre d’unité z. La méthode géodésique produit une pente plus précise que la méthode planaire.
Transformation de coordonnées géodésiques
Le système de coordonnées ECEF est un système de coordonnées cartésien 3D fondé sur la règle de la main droite avec le centre de la terre comme origine, où tout emplacement est représenté par les coordonnées X, Y et Z. La figure ci-dessous illustre un exemple d'emplacement cible T exprimé avec des coordonnées géocentriques.
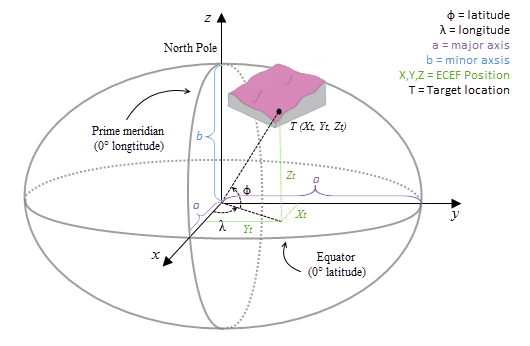
Le calcul géodésique utilise une coordonnée X, Y, Z qui est calculée en fonction de ses coordonnées géodésiques (latitude φ, longitude λ, hauteur h). Lorsque le système de coordonnées du raster de surface en entrée est un système de coordonnées projetées (SCP), le raster est d'abord re-projeté dans un système de coordonnées géographiques (SCG), où chaque emplacement possède une coordonnée géodésique, puis transformé en système de coordonnées ECEF. La hauteur h (valeur z) est la hauteur ellipsoïdale sur la surface de l'ellipsoïde. Reportez-vous aux illustrations ci-dessous.
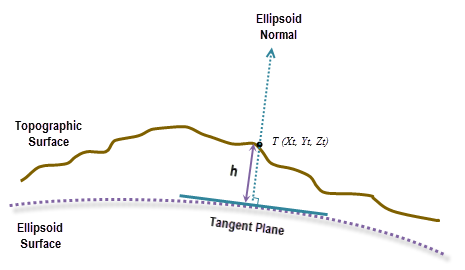
Pour effectuer la transformation en coordonnées ECEF à partir d'une coordonnée géodésique (latitude φ, longitude λ, hauteur h), utilisez les formules suivantes :
X = (N(φ)+h)cosφcosλY = (N(φ)+h)cosφsinλZ = (b2/a2*N(φ)+h)sinφ- où :
- N( φ ) = a2/ √(a2cosφ2+b2sinφ2)
- φ = latitude
- λ = longitude
- h = hauteur ellipsoïdale
- a = grand axe de l'ellipsoïde
- b = petit axe de l'ellipsoïde
La hauteur ellipsoïdale h est en mètres dans les formules ci-dessus. Si l'unité z de votre raster en entrée est spécifiée dans n'importe quelle autre unité, elle sera transformée en mètre.
Calcul de pente
La pente géodésique est l'angle formé entre la surface topographique et la surface de l'ellipsoïde. Toute surface parallèle à la surface de l'ellipsoïde a une pente de 0. Pour calculer la pente à chaque emplacement, un plan de voisinage de 3 cellules x 3 est adapté autour de chaque cellule de traitement à l'aide de la méthode des moindres carrés (LSM). Le meilleur ajustement par la méthode des moindres carrés (LSM) minimise la somme des carrés des différences (dzi) entre la valeur z réelle et la valeur z ajustée. L'illustration ci-dessous fournit un exemple.
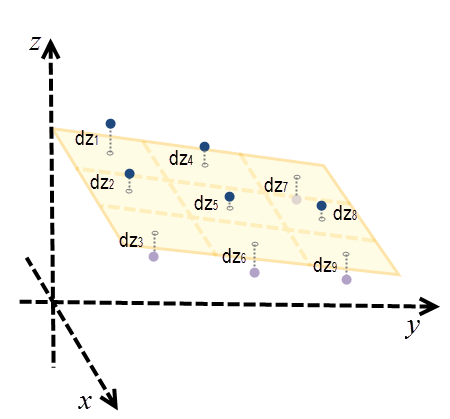
Ici, le plan est représenté par z = Ax + By + C. Pour chaque cellule centrale, dzi est la différence entre la valeur z réelle et la valeur z ajustée.
Le plan est mieux ajusté lorsque ∑9i=1dzi2 est minimisé.
Une fois le plan ajusté, la surface normale est calculée à l'emplacement de la cellule. Au même endroit, une normale à l’ellipsoïde perpendiculaire au plan tangent de la surface de l’ellipsoïde est également calculée.
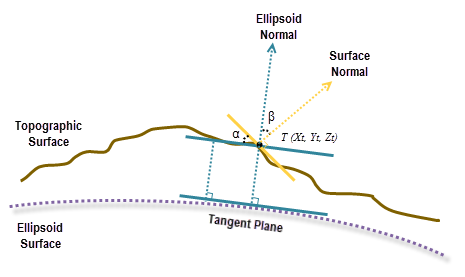
La pente, en degrés, est calculée à partir de l'angle entre la normale à l'ellipsoïde et la normale à la surface topographique, représentée par β ici. À partir de l'illustration ci-dessus, l'angle α est la pente géodésique, qui est identique à l'angle β, conformément à la loi de la congruence géométrique.
Pour calculer la pente en pourcentage, la formule suivante est utilisée :
Slope_PercentRise = ATAN(β) * 100%Puis-je utiliser l’outil Paramètres de surface ?
Si la valeur du paramètre Raster en entrée (in_raster dans Python) correspond à une résolution élevée avec une taille de cellule inférieure à quelques mètres, soit particulièrement bruyante, envisagez d’utiliser l’outil Paramètres de surface et son option de voisinage définie par l’utilisateur à la place du voisinage immédiat de 3 par 3 de cet outil. L’utilisation d’un voisinage plus grand peut minimiser l’effet de surfaces bruyantes. Elle contribue également à mieux représenter les reliefs et les caractéristiques de la surface lors de l’utilisation de surfaces de haute résolution.
Utiliser un GPU
Pour la méthode géodésique, cet outil propose des performances accrues si un certain matériel GPU est installé sur votre système. Reportez-vous à la section Traitement GPU avec Spatial Analyst pour en savoir plus sur sa prise en charge, sa configuration et son activation.
Bibliographie
Marcin Ligas, et Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159
B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice. Section 10.2.1. p. 282.
David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?