Fonctionnement de l’interpolation polynomiale globale

Disponible avec une licence Geostatistical Analyst.

L’interpolation polynomiale globale ajuste une surface lisse qui est définie par une fonction mathématique (un polynôme) aux points d'échantillonnage en entrée. La surface polynomiale globale évolue graduellement et capture une structure à échelle grossière dans les données.

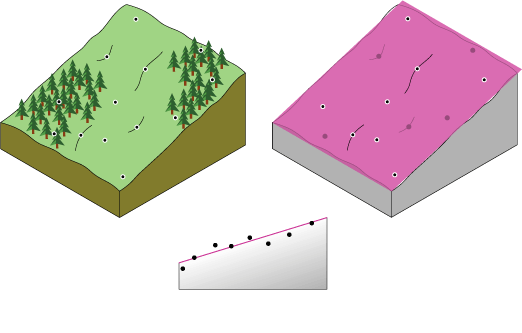
Théoriquement, l’interpolation polynomiale globale revient à prendre une feuille de papier et à l’ajuster entre les points placés en hauteur (élevés à la hauteur de la valeur). Cette méthode est illustrée dans le diagramme ci-dessous représentant un ensemble de points d’échantillonnage d’élévation, relevés sur une colline légèrement inclinée (la feuille de papier est de couleur magenta).

Mais une feuille de papier plate ne capturera pas un paysage contenant une vallée de manière exacte. Cependant, si vous êtes autorisé à la courber une fois, vous obtiendrez un meilleur ajustement. L’ajout d’un terme à la formule mathématique produit un résultat similaire : une courbure dans le plan. Une surface plane (pas de courbure sur la feuille de papier) est un polynôme de premier degré (linéaire). Si vous la courbez une fois, vous obtiendrez un polynôme de deuxième ordre (quadratique) et un polynôme de troisième ordre (cubique) si vous la courbez deux fois, et ainsi de suite. Geostatistical Analyst autorise jusqu’à 10 fois. L'image suivante présente, en théorie, un polynôme de deuxième degré ajusté à une vallée.

Il y a très peu de chances que la feuille de papier passe à travers les points mesurés réels, ce qui rend l’interpolation polynomiale globale inexacte. Certains points seront situés au-dessus de la feuille de papier, d’autres en dessous. Toutefois, si vous additionnez la proportion dans laquelle chaque point se situe au-dessus de la feuille de papier et en dessous de la feuille, les sommes devraient être similaires. La surface, en magenta, est obtenue à l’aide de l’ajustement régressif par moindres carrés. La surface obtenue minimise les différences au carré entre les valeurs élevées au carré et la feuille de papier.

Quand utiliser l’interpolation polynomiale globale

Le résultat de l’interpolation polynomiale globale est une surface lisse qui représente les tendances graduelles de la surface, sur la zone d’intérêt.

L’interpolation polynomiale globale est utilisée dans les cas suivants :

• L'ajustement d’une surface aux points d’échantillonnage lorsque la surface varie lentement d’une région à l’autre sur la zone d’intérêt (par exemple, la pollution d’une zone industrielle).
• L’analyse et/ou la suppression des effets des tendances à long terme ou globales. Dans de telles circonstances, la technique est souvent désignée sous le nom "d'analyse de surface de tendance".

L’interpolation polynomiale globale crée une surface qui évolue lentement, à l’aide de polynômes de premier ordre qui décrivent éventuellement un processus physique (tel que la pollution et la direction du vent). Cependant, il est à noter que plus le polynôme est complexe, plus il est difficile d’en interpréter les résultats physiques. De plus, les surfaces calculées sont extrêmement vulnérables aux points aberrants (valeurs extrêmement élevées ou extrêmement basses), en particulier sur les tronçons.