Utilisation de la validation croisée pour évaluer les résultats d’interpolation

Disponible avec une licence Geostatistical Analyst.

Avant de choisir un modèle d’interpolation pour la prise de décision, vous devez évaluer la qualité des prévisions effectuées par le modèle à de nouvelles localisations. Toutefois, si vous ne connaissez pas les véritables valeurs aux localisations situées entre les points mesurés, comment pouvez-vous savoir si les prévisions établies par le modèle sont précises et fiables ? Pour répondre à cette question, il semble que vous devriez connaître les valeurs des localisations que vous n’avez pas échantillonnées. Toutefois, une méthode courante et largement utilisée permet d’évaluer la précision et la fiabilité de l’interpolation : la validation croisée.

Validation croisée

La validation croisée est une méthode de rééchantillonnage de type leave-one-out (laisser un élément de côté) qui utilise d’abord tous les points en entrée pour estimer les paramètres d’un modèle d’interpolation (comme le semi-variogramme de krigeage ou la valeur de puissance de la pondération de l’inverse de la distance). Elle retire ensuite un point en entrée et utilise les points restants pour prévoir la valeur à la localisation du point masqué, puis la valeur prévue est comparée à la valeur mesurée. Le point masqué est ensuite réintégré dans le jeu de données et un autre point est masqué et prévu. Ce processus se répète pour tous les points en entrée.

Le diagramme ci-dessous illustre le processus de validation croisée pour un point. Une fois le modèle d’interpolation estimé à partir de tous les points bleus, la valeur du point rouge est masquée et les points restants sont utilisés pour prévoir la valeur du point masqué. La prévision est ensuite comparée à la valeur mesurée. Ce processus se répète tous les 10 points.

Un point rouge est masqué et la valeur est prévue à partir des points restants. Ce processus est répété pour tous les points.

La validation croisée permet d’évaluer efficacement les modèles d’interpolation, car elle simule la prévision des valeurs aux nouvelles localisations non mesurées ; les valeurs des localisations n’étant pas dépourvues de mesure, mais seulement masquées, les valeurs prévues peuvent être validées par rapport à leurs valeurs connues. Si le modèle peut prévoir avec précision les valeurs des points masqués, il doit alors être également capable de prévoir avec précision les valeurs aux nouvelles localisations non mesurées. Si, toutefois, les erreurs de validation croisée sont très importantes, vous devez vous attendre à des erreurs de la même envergure lors de la prévision aux nouvelles localisations.

La validation croisée est effectuée automatiquement lors de la création d’un modèle d’interpolation et les résultats s’affichent sur la dernière page de Geostatistical Wizard (Assistant géostatistique). La validation croisée peut également être calculée sur une couche géostatistique existante à l’aide de l’outil Validation croisée. Si une carte contient une couche géostatistique, vous pouvez afficher les statistiques de validation croisée en cliquant avec le bouton droit sur la couche et en sélectionnant Cross Validation (Validation croisée) ou en cliquant sur le bouton Cross Validation (Validation croisée) dans le menu du ruban Data (Données) de la couche géostatistique.

La validation croisée présente toutefois l’inconvénient d’utiliser initialement tous les points en entrée pour estimer les paramètres du modèle d’interpolation avant de masquer chaque point de manière séquentielle. Étant donné que tous les points contribuent à l’estimation des paramètres d’interpolation, ils ne sont pas entièrement masqués dans la procédure. Les points individuels n’ont généralement pas une grande influence sur les valeurs estimées des paramètres d’interpolation ; toutefois, dans le cas de jeux de données de petite taille et de jeux de données contenant des points aberrants, même un seul point peut modifier de manière significative les estimations des paramètres d’interpolation. Pour masquer entièrement les valeurs des points et éviter une double utilisation des données, vous pouvez faire appel à la validation.

Validation

La validation est similaire à la validation croisée, à la différence près qu’elle retire d’abord un sous-ensemble entier des points en entrée, appelé le jeu de données test. Elle utilise ensuite les points restants, appelés jeu de données d’entraînement, pour estimer les paramètres du modèle d’interpolation. Le modèle d’interpolation effectue alors des prévisions sur toutes les localisations du jeu de données test et les erreurs de validation sont calculées pour chaque point test. Puisque le jeu de données test n’est pas du tout utilisé pour estimer les paramètres d’interpolation ou effectuer des prévisions, la validation est la manière la plus rigoureuse qui permet d’estimer le degré de précision et de fiabilité des prévisions du modèle d’interpolation aux nouvelles localisations dépourvues de valeurs connues. La validation présente toutefois le gros inconvénient de ne pas utiliser toutes les données pour créer le modèle d’interpolation ; les estimations des paramètres risquent donc de ne pas être aussi précises que si vous aviez utilisé toutes les données. En raison de cette contrainte qui impose la réduction de la taille du jeu de données, la validation croisée est en général privilégiée à la validation sauf si les données sont suréchantillonnées.

Vous pouvez créer les jeux de données test et d’entraînement à l’aide de l’outil Sous-ensembles d’entités. Après avoir créé un modèle d’interpolation (couche géostatistique) sur le jeu de données d’entraînement, vous pouvez procéder à la validation à l’aide de l’outil Couche GA vers points. Indiquez la couche géostatistique créée à partir du jeu de données d’entraînement, effectuez les prévisions sur le jeu de données test et procédez à la validation sur le champ utilisé pour l’interpolation. Les erreurs de validation et d’autres statistiques de validation sont enregistrées dans la classe d’entités en sortie.

Le reste de cette rubrique ne traite que de la validation croisée, mais tous les concepts sont analogues dans le cas de la validation.

Statistiques de validation croisée

Lorsque vous effectuez une validation croisée, différentes statistiques sont calculées pour chaque point. Vous pouvez afficher ces statistiques sur l’onglet Table de la boîte de dialogue de validation croisée ou les enregistrer dans une classe d’entités à l’aide de l’outil Validation croisée. Les champs suivants sont créés pour chaque point :

• Measured (Mesuré) : valeur mesurée du point masqué.
• Predicted (Prévu) : valeur prévue par la validation croisée à la localisation du point masqué.
• Error (Erreur) : différence entre les valeurs prévue et mesurée (valeur prévue moins valeur mesurée). Une erreur positive signifie que la prévision est supérieure à la valeur mesurée et une erreur négative signifie que la prévision est inférieure à la valeur mesurée.
• Standard Error (Erreur standard) : erreur standard de la valeur prévue. Si les erreurs sont distribuées normalement, approximativement deux tiers des valeurs mesurées se situent dans une erreur standard de la valeur prévue et environ 95 % d’entre elles sont comprises dans deux erreurs standard.
• Standardized Error (Erreur standardisée) : erreur divisée par l’erreur standard. Si vous souhaitez utiliser des sorties de type quantile ou probabilité, les valeurs d’erreur standardisée doivent suivre une distribution normale standard (moyenne égale à zéro et écart type égal à un).

De plus, pour les modèles de krigeage bayésien empirique, les statistiques de validation croisée suivantes sont disponibles :

• Continuous Ranked Probability Score (Score de probabilité classé continu) : nombre positif mesurant l’exactitude et la précision de la valeur prévue, où une valeur moins élevée est privilégiée. La valeur en soi est difficile à interpréter, mais plus l’erreur est proche de zéro et plus l’erreur standard est faible, plus le score de probabilité classé continu est petit. Cette statistique mesure essentiellement une distance (il ne s’agit pas d’une distance géographique standard) entre la valeur mesurée et la distribution prévue, qui tient compte de la précision de la prévision et de l’erreur standard. Les distributions prévisionnelles étroites centrées autour de la valeur mesurée (erreur proche de zéro et faible erreur standard) ont des scores de probabilité classés continus proches de zéro. Cette valeur est mesurée en unités de données au carré et ne peut donc pas être comparées aux jeux de données dont les unités ou les plages de valeurs sont différentes.
• Validation Quantile (Quantile de validation) : quantile de la valeur mesurée par rapport à la distribution prévisionnelle. Si le modèle est correctement configuré, les quantiles de validation sont uniformément distribués entre 0 et 1 et n’affichent aucun modèle. Les quantiles de validation de modèles incorrectement configurés sont souvent agrégés au milieu (la plupart des valeurs sont proches de 0,5) ou aux extrêmes (la plupart des valeurs sont proches de 0 ou 1).
• Inside 90 Percent Interval (Dans un intervalle de 90 pour cent) : indicateur (1 ou 0) spécifiant si la valeur mesurée se situe dans un intervalle de prévision de 90 % (similaire à un intervalle de confiance). Si le modèle est correctement configuré, environ 90 % des points sont compris dans l’intervalle et ont une valeur de 1.
• Inside 95 Percent Interval (Dans un intervalle de 95 pour cent) : indicateur (1 ou 0) spécifiant si la valeur mesurée se situe dans un intervalle de prévision de 95 %. Si le modèle est correctement configuré, environ 95 % des points sont compris dans l’intervalle et ont une valeur de 1.

Remarque :

Les méthodes d’interpolation qui ne prennent pas en charge les sorties de type erreur standard de prévision peuvent uniquement calculer les valeurs mesurée, prévue et d’erreur.

Résumé statistique de validation croisée

Les statistiques de validation croisée individuelles de chaque point masqué fournissent des informations détaillées sur les performances du modèle, mais dans le cas d’un nombre élevé de points en entrée, il est nécessaire de synthétiser les informations pour pouvoir interpréter rapidement leur signification dans les résultats d’interpolation. Vous pouvez consulter les résumés statistiques de validation croisée sur l’onglet Summary (Résumé) de la boîte de dialogue de validation croisée ou sous la forme de messages dans l’outil Validation croisée. Les résumés statistiques suivants sont disponibles :

Remarque :

Dans toutes les formules, n représente le nombre de points. s_i représente la localisation du point masqué. z(s_i) est la valeur mesurée à la localisation. z accent circonflexe(s_i) est la valeur prévue. σ accent circonflexe est l’erreur standard de la valeur prévue.

• Mean Error (Erreur moyenne) : moyenne des erreurs de validation croisée. La valeur doit être aussi proche de zéro que possible. L’erreur moyenne mesure le biais du modèle ; une erreur moyenne positive indique une tendance à prévoir des valeurs trop élevées et une erreur moyenne négative une tendance à sous-estimer la prévision des valeurs mesurées. Cette statistique est calculée dans les unités des valeurs de données.
  • 
• Root Mean Square Error (Erreur quadratique moyenne) : racine carrée de la moyenne des erreurs de prévision au carré. Cette valeur doit être aussi faible que possible. La statistique mesure la précision de la prévision et la valeur se rapproche de l’écart moyen des valeurs prévues par rapport aux valeurs mesurées. La valeur est indiquée dans les unités des valeurs de données. Par exemple, dans le cas de l’interpolation des températures en degrés Celsius, une erreur quadratique moyenne de 1,5 signifie que les prévisions diffèrent en moyenne de 1,5 degré par rapport aux valeurs mesurées.
  • 
• Mean Standardized Error (Erreur standardisée moyenne) : moyenne des erreurs standardisées (erreur divisée par l’erreur standard). La valeur doit être aussi proche de zéro que possible. Cette statistique mesure le biais du modèle sur une échelle standardisée qui permet d’établir des comparaisons entre des jeux de données dotés de valeurs et d’unités différentes.
  • 
• Average Standard Error (Erreur standard moyenne) : moyenne quadratique des erreurs standard. Cette statistique mesure la précision du modèle, une tendance pour produire des distributions prévisionnelles proches étroitement centrées autour de la valeur prévue. La valeur doit être aussi faible que possible, mais également approximativement égale à l’erreur quadratique moyenne.
  • 
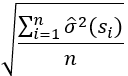
  • La moyenne est calculée sur les variances de la validation croisée (erreurs standard au carré) car les variances sont additives, mais les erreurs standard ne le sont pas.
• Root Mean Square Standardized Error (Erreur quadratique moyenne standardisée) : erreur quadratique moyenne des erreurs standardisées. Cette statistique mesure la précision des erreurs standard en comparant la variabilité des erreurs de validation croisée aux erreurs standard estimées. La valeur doit être aussi proche de 1 que possible. Les valeurs inférieures à 1 indiquent que les erreurs standard estimées sont trop élevées et les valeurs supérieures à 1 indiquent qu’elles sont trop faibles. Il est possible d’interpréter cette valeur comme un ratio inverse ; par exemple, une valeur de 3 signifie que les erreurs standard sont égales à un tiers des valeurs attendues, en moyenne. De même, une valeur de 0,5 signifie que les erreurs standard sont le double des valeurs attendues.
  • 

De plus, pour les modèles de krigeage bayésien empirique, les résumés statistiques de validation croisée suivants sont disponibles :

• Average CRPS (CRPS moyen) : moyenne des valeurs de score de probabilité classé continu (CRPS). Cette valeur doit être aussi faible que possible. Il est nécessaire d’estimer avec exactitude et précision les prévisions et les erreurs standard pour obtenir un modèle avec un CRPS moyen faible.
• Inside 90 Percent Interval (Dans un intervalle de 90 pour cent) : pourcentage des valeurs mesurées comprises dans un intervalle de prévision de 90 %. Cette valeur doit être proche de 90. Cette statistique mesure le degré de cohérence des erreurs standard avec les valeurs prévues. Les valeurs supérieures à 90 indiquent que les erreurs standard sont trop élevées par rapport aux valeurs prévues. Les valeurs inférieures à 90 indiquent que les erreurs standard sont trop faibles.
• Inside 95 Percent Interval (Dans un intervalle de 95 pour cent) : pourcentage des valeurs mesurées comprises dans un intervalle de prévision de 95 %. Cette valeur doit être proche de 95. Cette statistique mesure le degré de cohérence des erreurs standard avec les valeurs prévues.

Remarque :

Les méthodes d’interpolation qui ne prennent pas en charge les sorties de type erreur standard de prévision peuvent uniquement calculer les statistiques de type erreur moyenne et erreur quadratique moyenne.

Comparaison du modèle d’interpolation

La validation croisée peut être utilisée pour évaluer la qualité d’un modèle géostatistique, mais elle est également couramment employée pour comparer deux modèles candidats ou plus dans le but de déterminer celui que vous utiliserez dans une analyse. Si le nombre de modèles candidats est réduit, vous pouvez les explorer dans plusieurs boîtes de dialogue de validation croisée. En alignant les boîtes de dialogue côte à côte, vous pouvez consulter tous les résultats en même temps et examiner en détail chaque modèle.

Cependant, dans le cas d’un grand nombre de modèles candidats ou lorsque la création de modèle est automatisée, l’outil Comparer des couches géostatistiques permet de comparer et de classer automatiquement les modèles selon des critères personnalisables. Vous pouvez classer les modèles en fonction d’un seul critère (comme la plus petite erreur quadratique moyenne ou l’erreur moyenne la plus proche de zéro), en fonction des classements moyens pondérés de plusieurs critères ou en fonction du tri hiérarchique de plusieurs critères (où les rattachements de chaque critère sont rompus par les critères suivants de la hiérarchie). Il est également possible d’utiliser des critères d’exclusion pour exclure de la comparaison les résultats d’interpolation qui ne répondent pas à des normes de qualité minimales. L’outil Interpolation exploratoire peut également effectuer les mêmes comparaisons de validation croisée, mais il génère automatiquement les couches géostatistiques à partir d’un jeu de données et d’un champ. Cet outil permet de déterminer rapidement les méthodes d’interpolation les plus performantes en fonction des données dont vous disposez sans qu’il soit nécessaire de les exécuter individuellement.

Diagrammes de validation croisée

La boîte de dialogue contextuelle de validation croisée propose différents diagrammes qui permettent de visualiser et d’explorer les statistiques de validation croisée de manière interactive. La section des diagrammes de la boîte de dialogue contient cinq onglets principaux, chacun affichant un diagramme différent.

L’onglet Predicted (Prévu) affiche les valeurs prévues par rapport aux valeurs mesurées dans un nuage de points avec une ligne de régression bleue ajustée aux données. Étant donné que les valeurs prévues doivent être égales aux valeurs mesurées, une ligne de référence est fournie pour indiquer dans quelle mesure la ligne de régression se rapproche de cet idéal. Toutefois, en pratique, la ligne de régression a une pente plus raide que la ligne de référence, car les modèles d’interpolation (et en particulier le krigeage) tendent à lisser les valeurs de données, ou sous-estimant les valeurs élevées et en surestimant les valeurs faibles.

Remarque :

La valeur Regression function (Fonction de régression) située sous le nuage de points est calculée selon une procédure de régression fiable. Cette procédure ajuste tout d’abord une ligne de régression linéaire standard au nuage de points. Ensuite, tous les points situés à plus de 2 écarts types au-dessus et au-dessous de la ligne de régression sont retirés et une nouvelle équation de régression est calculée. Cela permet de garantir qu’un petit nombre de points aberrants ne déforment pas les estimations de la pente et de l’intersection. Tous les points sont affichés dans le nuage de points, même s’ils ne sont pas utilisés pour estimer la fonction de régression.

Les onglets Error (Erreur) et Standardized Error (Erreur standardisée) sont similaires à l’onglet Predicted (Prévu), mais ils représentent les erreurs et les erreurs standardisées de la validation croisée par rapport aux valeurs mesurées. Dans ces diagrammes, la ligne de régression devrait être plate et les points ne devraient afficher aucun modèle. Toutefois, dans la pratique, les pentes sont généralement négatives en raison du lissage.

L’onglet Normal QQ Plot (Diagramme QQ normal) affiche un nuage de points des erreurs standardisées par rapport au quantile équivalent d’une distribution normale standard. Si les erreurs de validation croisée sont normalement distribuées et que les erreurs standard sont estimées de manière exacte, les points du diagramme doivent tous être proches de la ligne de référence. Il est très important de consulter ce diagramme lorsque vous utilisez des sorties de type quantile ou probabilité car elles requièrent des erreurs normalement distribuées.

L’onglet Distribution affiche les distributions des statistiques de validation croisée (estimées à l’aide de la densité de noyau). Utilisez le menu déroulant Field (Champ) pour changer la statistique affichée. Une option particulièrement utile (représentée dans l’image ci-dessous) consiste à superposer les distributions des valeurs mesurées et prévues sur le même diagramme et d’examiner dans quelle mesure elles sont alignées. Ces deux distributions doivent être aussi similaires que possible ; toutefois, la distribution prévue est généralement plus grande et plus étroite que la distribution mesurée en raison du lissage.

Interprétation en contexte des statistiques de validation croisée

On pense souvent à tort que la validation croisée et les autres procédures de validation de modèle sont conçues pour déterminer si le modèle est correct pour les données. En réalité, les modèles ne sont jamais corrects pour les données collectées dans le monde réel, mais ils n’ont pas besoin d’être corrects pour fournir des informations utiles en vue d’une prise de décision. Ce concept est résumé par la célèbre citation de George Box (1978) : « Tous les modèles sont faux, mais certains sont utiles. » Pensez à la validation croisée comme un moyen de quantifier l’utilité d’un modèle et non comme une liste de contrôle visant à déterminer si un modèle est correct. Grâce aux nombreuses statistiques disponibles (valeurs individuelles, résumés statistiques et diagrammes), un examen trop approfondi est susceptible de révéler des problèmes et des écarts des valeurs idéales et des modèles. Les modèles ne sont jamais parfaits, car ils ne représentent jamais parfaitement les données.

Lorsque vous examinez des résultats de validation croisée, il est important de garder en tête les objectifs et les attentes de l’analyse. Supposez, par exemple, que vous interpolez les températures en degrés Celsius pour effectuer des recommandations de santé publique pendant une vague de chaleur. Dans ce scénario, comment interpréter une valeur d’erreur moyenne de 0,1 ? Littéralement, cela signifie que le modèle a un biais positif et tend à surestimer les valeurs de température. Cependant, le biais moyen n’est que d’un dixième de degré, ce qui n’est pas assez important pour être pertinent dans le cadre d’une politique de santé publique. D’un autre côté, une valeur d’erreur quadratique moyenne de 10 degrés signifie qu’en moyenne, les valeurs prévues sont supérieures de 10 degrés aux températures réelles. Ce modèle est donc susceptible d’être trop imprécis pour être utile, car des différences de 10 degrés entraîneraient de grandes modifications dans les recommandations de santé publique.

Il est également important de savoir si vous avez l’intention de créer des intervalles de confiance ou des marges d’erreur pour les valeurs prévues. Vous pouvez ainsi prévoir une valeur de température de 28 degrés, plus ou moins deux degrés. Si vous n’envisagez pas de créer des marges d’erreur, les statistiques liées à l’erreur standard sont moins importantes, car leur objectif principal consiste à déterminer la précision des marges d’erreur. Alors que les problèmes de précision des erreurs standard peuvent parfois générer des valeurs prévues erronées, il est fréquent que les modèles d’interpolation effectuent des prévisions exactes, mais estiment les marges d’erreur de manière inexacte.

Les modèles d’interpolation ont de grandes difficultés à modéliser les valeurs extrêmes, à savoir les valeurs minimale et maximale d’un jeu de données. Les modèles d’interpolation effectuent des prévisions en utilisant les moyennes pondérées des valeurs mesurées dans le voisinage de la localisation de la prévision. Puisqu’elles s’appuient sur la moyenne des valeurs de données, les prévisions sont tirées vers la valeur moyenne des points du voisinage, phénomène appelé lissage. Le lissage est présent à divers degrés dans quasiment tous les modèles d’interpolation et peut être observé dans les pentes des différents diagrammes de validation croisée. Il est conseillé de minimiser le lissage, mais en pratique, ne vous fiez pas aux prévisions dans les zones proches des valeurs de données minimale et maximale.

Enfin, vos attentes en termes de résultats de validation croisée doivent dépendre de la qualité et du volume des données. S’il n’existe que quelques points ou si de grandes distances séparent les points, vous devez vous attendre à ce que les statistiques de validation croisée reflètent les informations limitées disponibles pour ces points. Même avec un modèle correctement configuré, les erreurs de validation croisée sont toujours importantes si les informations disponibles du jeu de données ne sont pas suffisantes pour l’établissement de prévisions précises. De manière similaire, si vous disposez d’une quantité importante d’informations et de données représentatives, même les modèles mal configurés dotés de paramètres inexacts peuvent produire des prévisions fiables et précises.