Les outils IA de série chronologique de la boîte à outils GeoAI utilisent des modèles de prévision de séries chronologiques basés sur le Deep Learning pour prévoir les valeurs futures à chaque emplacement dans un cube spatio-temporel. Ces modèles sont entraînés à l’aide de l’outil Entraîner le modèle de prévision de séries chronologiques sur des données de séries chronologiques existantes, et les modèles entraînés peuvent être utilisés pour prévoir à l’aide de l’outil Prévoir à l’aide d’un modèle de série chronologique. La sortie principale est une carte de l’intervalle temporel final prévu, ainsi que des messages d’information et des diagrammes contextuels. D’autres variables explicatives peuvent être fournies pour améliorer la prévision de la variable d’analyse.
Les outils utilisent différents types de réseaux neuronaux profonds pour la prévision de séries chronologiques. L’architecture de réseau prise en charge comprend des réseaux entièrement connectés ainsi que des réseaux neuronaux convolutifs et une mémoire LSTM (Long Short-Term Memory) pour la prévision de séries chronologiques. Les détails des architectures de modèle sont décrits par la suite.
Les données d’entraînement utilisées pour entraîner les modèles sont générées à l’aide de fenêtres horaires sur chaque variable des données de série temporaire en entrée. Les données de série chronologique peuvent suivre des tendances complexes et présenter plusieurs niveaux de saisonnalité. Les modèles basés sur le Deep Learning ont une capacité élevée à apprendre et peuvent apprendre ces modèles dans différents types de série chronologique et différents emplacements, à condition que les données d’entraînement existent en quantités suffisantes. L’outil d’entraînement entraîne un modèle de prévision global unique qui utilise les données d’entraînement de chaque emplacement. Ce modèle global est utilisé pour prévoir les valeurs futures à chaque emplacement à l’aide de l’outil de prévision.
Applications possibles
Les modèles basés sur le Deep Learning peuvent apprendre des tendances complexes de données et sont donc utilisés dans de nombreux contextes. Ils sont plus efficaces que d’autres méthodes de prévision lorsque les données présentent des tendances complexes ou une saisonnalité complexe, et lorsqu’une quantité suffisante de données d’entraînement est disponible pour apprendre ces relations.
Par exemple, vous pouvez utiliser le jeu d’outils IA de série chronologique dans les scénarios suivants :
- Un responsable de commerce au détail peut prévoir la demande en produits de consommation en fonction des données commerciales historiques et maintenir les stocks en conséquence.
- Un épidémiologiste peut modéliser l’augmentation des maladies infectieuses et prévoir le nombre de patients qui devront être hospitalisés dans la semaine à venir.
- Une centrale éolienne peut prévoir la quantité d’énergie éolienne qui sera produite en fonction des tendances historiques et des données météorologiques.
- Un investisseur immobilier peut examiner les tendances dans les prix de l’immobilier en fonction des données historiques et de leurs relations avec des facteurs tels que les taux de prêt, le prix de l’or et les indicateurs boursiers.
- Les législateurs peuvent prévoir la demande en logements, en électricité et en eau dans les zones urbaines.
- Les météorologistes peuvent prévoir l’oscillation australe d’El Niño en fonction des variables et des indices climatiques tels que les vents et les températures à la surface de la mer et dans l’océan Pacifique tropical Est.
Entraînement de modèle et prévision
L’outil Entraîner le modèle de prévision de séries chronologiques est utilisé pour entraîner un modèle de prévision de séries chronologiques basé sur le Deep Learning sur des données d’historique. Une ou plusieurs variables peuvent servir de variables explicatives et le modèle utilise des intervalles de données historiques à travers les emplacements pour apprendre les tendances, la saisonnalité, les modèles et les relations entre les données passées et la valeur de la variable d’analyse à des intervalles temporels ultérieurs.
L’erreur (également nommée perte) survenant dans la prévision est utilisée pour guider la formation du modèle à l’aide d’une descente de gradient. Le modèle s’améliore graduellement sur plusieurs cycles d’entraînement sur l’ensemble des données (époques) et l’erreur calculée (différence entre la prévision et la valeur de réalité de terrain à l’intervalle temporel suivant) diminue à mesure que l’entraînement progresse. Par défaut, l’entraînement du modèle s’arrête lorsque la perte des données de validation n’enregistre aucune amélioration après cinq époques consécutives, sauf si le paramètre Arrêter l’entraînement lorsque le modèle ne s’améliore plus n’est pas sélectionné. Le modèle entraîné est enregistré en tant que paquetage de Deep Learning (.dlpk) et peut être utilisé pour effectuer des prévisions sur des données de série chronologique invisibles avec l’outil Prévoir à l’aide d’un modèle de série chronologique.
Architectures de modèle
Les architectures de modèle prises en charge sont décrites ci-dessous.
LSTM (Long Short-Term Memory)
Les données de série chronologique sont de nature temporelle ou séquentielle, ce qui peut être géré par des réseaux neuronaux récurrents (RNN). Les réseaux RNN se souviennent des informations passées et les transmettent à l’état en entrée actuel. Toutefois, les réseaux RNN ordinaires ne sont pas en mesure de se souvenir des dépendances à long terme en raison de gradients qui disparaissent. La mémoire LSTM est un type de réseau RNN mis à niveau et permet de résoudre ce problème. Elle consiste en unités, chacune comportant quatre réseaux neuronaux, qui sont utilisées pour mettre à jour son état de cellule à l’aide des informations issues des entrées nouvelles et des sorties passées.
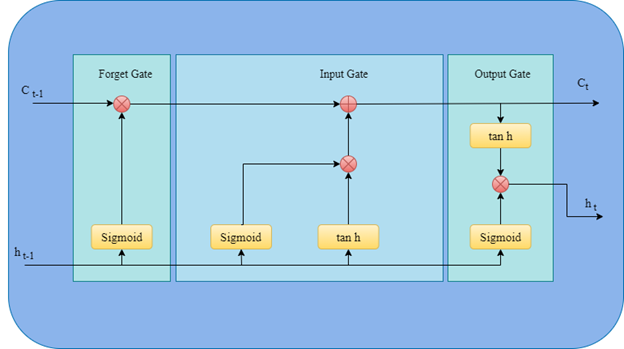
Lorsque vous définissez la valeur du paramètre Type de modèle sur LSTM, l’argument de modèle suivant peut être fourni pour personnaliser le modèle lorsque les valeurs par défaut ne sont pas utilisées :
| Nom | Valeur par défaut | Description |
|---|---|---|
hidden_layer_size | 100 | La taille de la couche masquée. |
Réseau entièrement convolutif (FCN, Fully Convolutional Network)
Les réseaux entièrement convolutifs (FCN, Fully Convolutional Network) s’utilisent essentiellement pour les images dans le cas de problèmes de segmentation sémantique et autre problème de vision informatique. Ils prennent une image en tant qu’entrée et la soumettent à une série de couches convolutives pour extraire les caractéristiques importantes. Ces réseaux neuronaux sont également capables d’extraire les tendances et la saisonnalité dans des données de série chronologique et de produire des résultats étonnamment bons dans la prévision de séries chronologiques. Un filtre unidimensionnel est appliqué aux données de série chronologique dans chaque couche convolutive pour extraire les entités discriminantes sans variation dans le temps avec une capacité prédictive élevée.
En termes de calculs, les couches convolutives sont efficaces en raison de leurs paramètres réduits, car la connectivité locale est assurée entre les couches en entrée et en sortie. Le partage des paramètres réduit aussi significativement le nombre de paramètres requis car les filtres possèdent tous la même pondération de noyau. L’avantage le plus évident lié aux réseaux neuronaux convolutifs réside dans l’invariance des transformations, qui rend le réseau robuste lors de la détection d’entités importantes indépendamment de leur emplacement au sein des données.
Le modèle de série chronologique FCN utilise trois couches de convolution 1D sans arpentage ni groupage. Le groupage moyen est effectué sur la dernière couche de l’architecture. Après chaque convolution, une normalisation par lots est effectuée et des unités linéaires rectifiées (ReLU, Rectified Linear Unit) sont utilisées en tant que fonctions d’activation. L’architecture du réseau se décrit comme suit :

InceptionTime
Ce réseau CNN (Convolutional Neural Network, réseau neuronal convolutif) est basé sur le réseau de lancement précédemment proposé (« Going Deeper with Convolutions » (2015) [1]) pour la classification d’image. Avant la valeur InceptionTime, la puissance de calcul des réseaux neuronaux reposait sur leur profondeur. Le module de lancement proposé dans cet article utilise diverses convolutions en parallèle et concatène leur sortie, augmentant ainsi à la fois la profondeur et la largeur du réseau tout en maintenant le budget de calcul constant.
Le modèle InceptionTime applique cette architecture pour la prévision de séries chronologiques. Dans ce modèle, la concaténation est effectuée pour des couches de convolution à une dimension de longueurs de noyau 10, 20 et 40, et une couche de groupage de taille maximum 3. De plus, une connexion résiduelle est introduite à chaque troisième mode de lancement, comme l’illustre la figure suivante. Le réseau de lancement utilise aussi largement des couches d’étranglement, où des filtres de longueur 1 et de pas 1 sont appliqués pour réduire la dimensionnalité des séries chronologiques et la complexité du modèle, tout en prévenant le sur-ajustement. Plusieurs de ces blocs de lancement sont utilisés sur le réseau, suivis d’une couche de groupage moyen global.
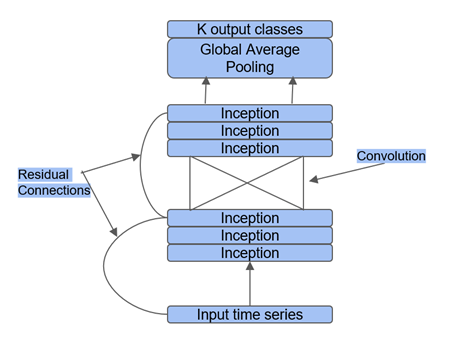
ResNet
La sagesse traditionnelle à propos du réseau neuronal profond est que plus il est profond, plus il devrait être performant car il existe davantage de paramètres pour apprendre les tâches complexes. Toutefois, il a été observé que les performances du modèle se dégradent avec une plus grande profondeur en raison du problème de gradients qui disparaissent. Pour résoudre ce problème, un bloc résiduel a été introduit dans l’architecture ResNet. Ce modèle est composé de blocs résiduels, auxquels sont ajoutées des connexions d’omission, ou connexions de raccourci. Ces connexions directes permettent au gradient de circuler sans entraves vers les couches précédentes du réseau qui les accompagnent pour mieux apprendre.
Pour la prévision de séries chronologiques, l’architecture est adaptée dans l’article « Time Series Classification from Scratch with Deep Neural Networks: A Strong Baseline » de Wang et. al. 2016. Le réseau utilise trois blocs résiduels, comme l’illustre la figure suivante. Chaque bloc contient une combinaison de trois convolutions avec normalisation par lots et utilise des unités ReLU comme fonction d’activation. Des connexions d’omission sont ajoutées en entrée et en sortie. Les tailles de filtres utilisées ici ont pour longueur 64, 128 et 128, respectivement, la dernière couche utilisant le groupage moyen global.

ResCNN
Ce réseau combine des réseaux ResNet à des réseaux neuronaux convolutifs. Une connexion d’omission unique est ajoutée au réseau pour améliorer le transfert des informations. Pour éliminer le sur-ajustement lié aux connexions d’omission dans tous les blocs résiduels, cette architecture n’utilise une connexion d’omission que dans le premier bloc, comme l’illustre la figure suivante. Des fonctions d’activation diverses, telles que ReLU, LReLU, PReLU et ELU, sont utilisées dans différentes couches pour obtenir une abstraction correcte [2].

Prévision et validation
Pour vérifier l’efficacité du modèle, l’outil fait appel à deux mesures. La première est la mesure de prévision et la seconde la mesure de validation. La mesure de prévision permet d’estimer l’adéquation de la prévision par rapport aux données existantes, tandis que la mesure de validation fournit des informations sur l’efficacité avec laquelle le modèle prévoit les données de validation mises de côté pendant son entraînement.
- Mesure de prévision
L’outil entraîne un modèle unique en combinant les données issues de différents emplacements d’un cube spatio-temporel et le modèle apprend les entités marquantes des données à chaque emplacement. Le modèle entraîné est alors utilisé pour prévoir dans des intervalles futurs. L’ajustement du modèle sur les données d’entraînement existantes est mesuré à l’aide de la racine carrée de l’erreur quadratique moyenne (EQM), qui est égale à la racine carrée de la différence au carré moyenne entre les valeurs apprises par le modèle et les valeurs réelles de la série chronologique.

T est le nombre d’intervalles temporels, ct la valeur apprise par le modèle et rt la valeur brute de la série chronologique à l’instant t.
L’image suivante montre les valeurs brutes d’une série chronologique associée aux valeurs apprises par le modèle de série chronologique. L’EQM de prévision mesure l’écart entre ces deux séries chronologiques.
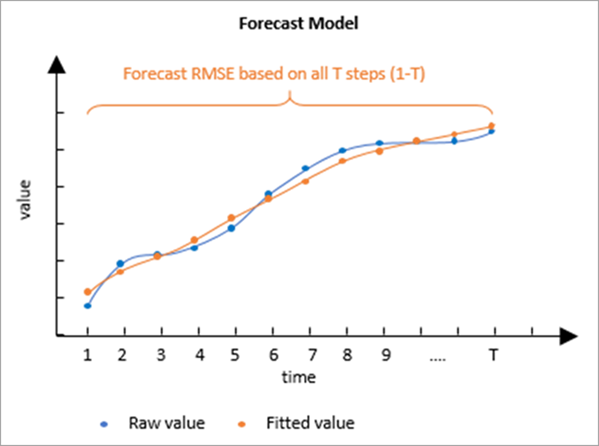
L’EQM de prévision ne mesure que le degré d’ajustement de la courbe aux valeurs brutes de la série chronologique. Il ne mesure pas la qualité des prévisions des valeurs futures par le modèle entraîné. Il est courant qu’un modèle s’ajuste bien à une série chronologique, mais qu’il ne fournisse pas de prévisions exactes après l’extrapolation. Pour cette raison, l’EQM de validation est une mesure plus fiable.
- Mesure de validation
Le modèle de validation est utilisé pour déterminer l’aptitude du modèle de prévision à prévoir les valeurs futures de chaque série chronologique. Il est construit en excluant certains des intervalles temporels finaux de chaque série chronologique et en entraînant le modèle avec les données non exclues. Ce modèle est ensuite utilisé pour prévoir les valeurs des données ayant été retenues, et les valeurs prévues sont comparées aux valeurs brutes qui étaient masquées. Par défaut, 10 pour cent des intervalles temporels sont retenus pour validation, mais ce nombre peut évoluer à l’aide du paramètre Numer of Time Steps to Exclude for Validation (Nombre d’intervalles temporels à exclure pour la validation). Le nombre de pas de temps exclus ne peut pas dépasser 25 % du nombre de pas de temps, et aucune validation n’est effectuée si une valeur de 0 est spécifiée. La précision des prévisions est mesurée par le calcul d’une statistique d’EQM de validation, qui est égale à la racine carrée de la différence quadratique moyenne entre les valeurs prévues et les valeurs brutes des pas de temps exclus.
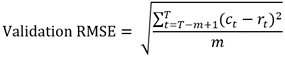
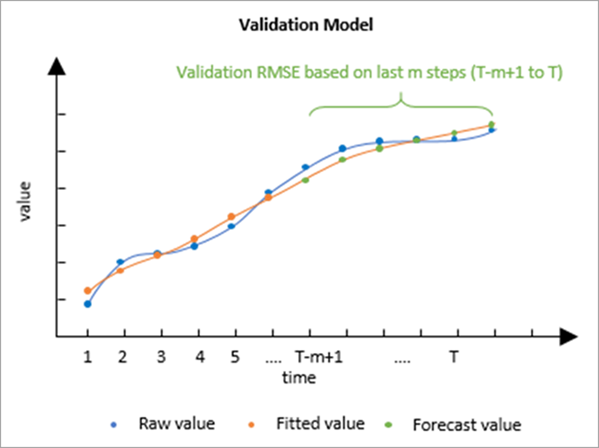
T est le nombre d’intervalles temporels, m est le nombre d’intervalles temporels retenus pour la validation, ct est la valeur prévue à partir des premiers T-m intervalles temporels, et rt est la valeur brute de la série chronologique retenue pour la validation au moment t.
L’image suivante montre les valeurs ajustées par le modèle à la première moitié d’une série chronologique et extrapolées pour prévoir la seconde moitié de la série chronologique. L’EQM de validation mesure l’écart entre les valeurs prévues et les valeurs brutes aux pas de temps retenus.
Sorties de l’outil
La principale sortie de cet outil est une classe d’entités 2D montrant chaque emplacement dans le cube spatio-temporel en entrée symbolisée par le pas de temps final prévu, les prévisions pour tous les autres pas de temps étant stockées sous forme de champs. Bien que chaque localisation soit prévue indépendamment et que les relations spatiales ne soient pas prises en compte, la carte peut afficher des modèles spatiaux pour des zones ayant des séries chronologiques similaires.
Diagrammes contextuels
Si vous cliquez sur une entité de la carte à l’aide de l’outil de navigation Explorer, un graphique s’affiche dans la vue Fenêtre contextuelle qui indique les valeurs du cube spatio-temporel ainsi que les valeurs ajustées et les valeurs prévues. Les valeurs du cube spatio-temporel apparaissent en bleu et sont reliées par une ligne bleue. Les valeurs ajustées apparaissent en orange et sont reliées par une ligne pointillée orange. Les valeurs prévues apparaissent en orange et sont reliées par une ligne unie orange qui représente la prévision du modèle de forêt. Vous pouvez survoler un point dans le diagramme pour afficher sa date et sa valeur.
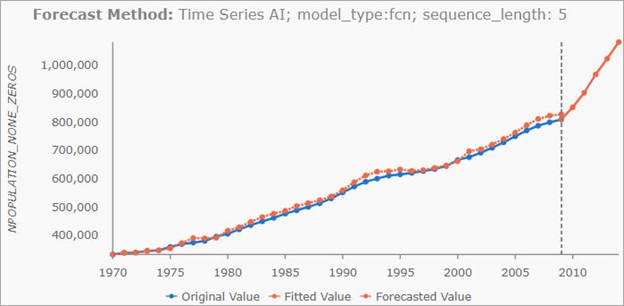
Le diagramme contextuel affiche les valeurs d’origine, les valeurs ajustées et les valeurs prévues.
Messages de géotraitement
L’outil fournit un certain nombre de messages d’informations sur l’exécution de l’outil. Les messages comportent trois sections principales.
La section Input Space Time Cube Details (Détails du cube spatio-temporel en entrée) présente les propriétés du cube spatio-temporel en entrée, ainsi que des informations sur le nombre d’intervalles temporels, le nombre de localisations et le nombre de groupes spatio-temporels. Les propriétés affichées dans cette première section dépendent de la façon dont le cube a été créé à l’origine, de sorte que les informations varient d’un cube à l’autre. La section Analysis Details (Détails d’analyse) affiche les propriétés des résultats des prévisions, y compris le nombre de pas de temps prévus, le nombre de pas de temps exclus pour la validation et des informations sur les pas de temps prévus.
La section Summary of Accuracy across Locations (Récapitulatif de la précision pour chaque emplacement) affiche un résumé statistique pour l’EQM de prévision et l’EQM de validation pour tous les emplacements. Pour chaque valeur, le minimum, le maximum, la moyenne, la médiane et l’écart type sont indiqués.
Remarque :
Les messages de géotraitement apparaissent au bas de la fenêtre Géotraitement pendant l’exécution de l’outil. Vous pouvez accéder aux messages en survolant la barre de progression, en cliquant sur le bouton contextuel  ou en développant la section des messages dans la fenêtre Géotraitement. Vous pouvez également consulter les messages de l’exécution précédente d’un outil dans l’historique de géotraitement.
ou en développant la section des messages dans la fenêtre Géotraitement. Vous pouvez également consulter les messages de l’exécution précédente d’un outil dans l’historique de géotraitement.
Champs en sortie
Outre les champs de géométrie ID d’objet et le champ contenant les diagrammes contextuels, les Entités en sortie comprennent les champs suivants.
- ID d’emplacement (LOCATION) : ID de l’emplacement correspondant du cube spatio-temporel.
- Prévision de (variable d’analyse) pour (intervalle temporel) (FCAST_1, FCAST_2, etc.) : valeur prévue de chaque intervalle temporel futur. L’alias du champ affiche le nom de la Analysis Variable (Variable d’analyse) et la date de la prévision. Un champ de ce type est créé pour chaque pas de temps prévu.
- Racine carrée de l’erreur quadratique moyenne de prévision (F_RMSE) : l’EQM de prévision.
- Racine carrée de l’erreur quadratique moyenne de validation (V_RMSE) : l’EQM de validation. Si aucun pas de temps n’a été exclu pour la validation, ce champ n’est pas créé.
- Méthode de prévision (METHOD) : champ de texte affichant le type de modèle d’IA de série chronologique utilisé et la longueur de la séquence.
Bibliographie
Pour plus d’informations sur les modèles de prévision de séries chronologiques basés sur le Deep Learning, reportez-vous aux références suivantes :
- Szegedy, Christian, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke et Andrew Rabinovich. « Going deeper with convolutions » Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1-9. 2015.
- Ismail Fawaz, Hassan, Benjamin Lucas, Germain Forestier, Charlotte Pelletier, Daniel F. Schmidt, Jonathan Weber, Geoffrey I. Webb, Lhassane Idoumghar, Pierre-Alain Muller et François Petitjean. « Inceptiontime: Finding alexnet for time series classification » Data Mining and Knowledge Discovery 34, no. 6 (2020) : 1936-1962.
- Wang, Zhiguang, Weizhong Yan et Tim Oates. « Time series classification from scratch with deep neural networks: A strong baseline. » 2017 International joint conference on neural networks (IJCNN), pages 1578-1585. IEEE, 2017.
- Zou, Xiaowu, Zidong Wang, Qi Li et Weiguo Sheng. « Integration of residual network and convolutional neural network along with various activation functions and global pooling for time series classification » Neurocomputing 367 (2019) : 39-45.
- Hochreiter, Sepp et Jürgen Schmidhuber. « Long short-term memory » Neural computation 9, no. 8 (1997) : 1735-1780.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?