Disponible avec une licence Spatial Analyst.
Disponible avec une licence 3D Analyst.
L’outil Paramètres de surface détermine les paramètres d’une surface raster tels que l’aspect, la pente et la courbure.
Exposition
Le paramètre de surface Aspect (Exposition) identifie la direction dans laquelle la pente descendante est orientée. La valeur de chaque cellule du raster en sortie indique la direction de boussole dans laquelle la surface est orientée à cet emplacement. La mesure s'effectue dans le sens horaire en degrés de 0 (plein nord) à 360 (plein nord également), ce qui trace un cercle plein. La valeur -1 est attribuée aux zones plates qui ne possèdent pas de pente descendante.

Les images suivantes illustrent un jeu de données d'altitude en entrée et le raster d'aspect en sortie.

Applications de l’aspect
Le paramètre de surface Aspect (Exposition) vous permet de réaliser les opérations suivantes :
- Détecter toutes les pentes faisant face au nord sur une montagne dans le cadre d'une recherche des pentes les plus appropriées à des pistes de ski.
- Calculer l'éclairage solaire de chaque emplacement d'une région dans le cadre d'une étude visant à déterminer la diversité de la vie sur chaque site.
- Détecter toutes les pentes exposées au sud dans une région montagneuse pour identifier les emplacements où la neige est susceptible de fondre plus rapidement dans le cadre d'une étude visant à connaître les emplacements résidentiels qui seront probablement touchés en premier par l'écoulement.
Calcul de l’exposition géodésique
L’exposition géodésique à un emplacement est la direction angulaire α de la surface de la pente descendante par rapport au nord, mesurée sur un plan tangent à la surface de l’ellipsoïde (plan bleu dans l’illustration ci-dessous).
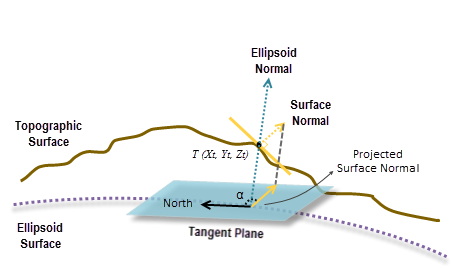
Pour le calcul de l’exposition à chaque emplacement, une surface quadratique ou biquadratique est adaptée aux cellules de voisinage grâce à la méthode des moindres carrés (LSM). Une normale à la surface est calculée à l’emplacement de la cellule à partir de cette surface. Au même endroit, une normale à l’ellipsoïde perpendiculaire au plan tangent de la surface de l’ellipsoïde est également calculée.
Comme le plan tangent de la surface ellipsoïde est considéré comme le plan de référence, la normale à la surface est projetée sur le plan. Finalement, l’exposition géodésique se calcule en mesurant l’angle α dans le sens horaire entre le nord et la projection de la normale à la surface (reportez-vous à l’illustration ci-dessus).
Pente
Le paramètre de surface Slope (Pente) correspond à la déclivité de chaque cellule d’une surface raster. Plus la valeur de la pente est faible, plus le terrain est plat ; plus la valeur de la pente est élevée, plus le terrain est pentu.
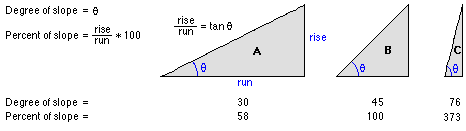
Le raster de pente en sortie peut être calculé dans deux unités : degrés ou pourcentage (pourcentage d’élévation). Pour mieux comprendre le pourcentage d’élévation, considérez-le comme la hauteur calculée divisée par le parcours, multipliée par 100. Consultez le triangle B ci-dessous. Lorsque l'angle est de 45 degrés, la hauteur calculée est égale au parcours et le pourcentage d'élévation est de 100 pour cent. Lorsque l'angle de pente se rapproche de la verticale (90 degrés), comme dans le triangle C, le pourcentage d'élévation se rapproche de l'infini.
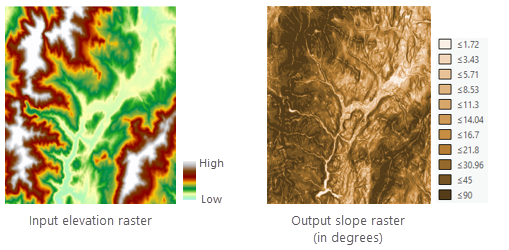
La pente est généralement appliquée à un jeu de données d’altitude, comme le montrent les images ci-dessous. Les pentes les plus raides apparaissent sur le raster de pente en sortie sous forme de couleur marron foncé ombré.
L'outil peut également être utilisé avec d'autres types de données continues, telles que des données de population, afin d'identifier d'importantes variations de valeur.
Calculs de pente géodésique
La pente géodésique est l'angle formé entre la surface topographique et la surface de l'ellipsoïde. Toute surface parallèle à la surface de l'ellipsoïde a une pente de 0. Pour le calcul de la pente à chaque emplacement, une surface quadratique ou biquadratique est adaptée aux cellules de voisinage grâce à la méthode des moindres carrés (LSM). Une normale à la surface est calculée à l’emplacement de la cellule à partir de cette surface. Au même endroit, une normale à l’ellipsoïde perpendiculaire au plan tangent de la surface de l’ellipsoïde est également calculée. La pente, en degrés, est calculée à partir de l’angle entre la normale à l’ellipsoïde et la normale à la surface topographique. Cet angle est identique entre la surface topographique et la surface de l’ellipsoïde.
Présentation de la courbure des surfaces
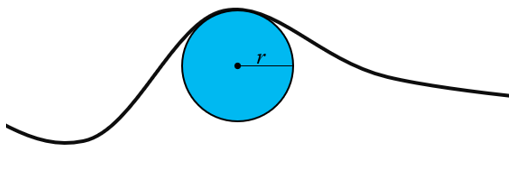
La courbure est un ensemble de types de paramètres de surface utilisés pour décrire la forme d’une surface, généralement le long d’une ligne à la surface, créée par l’intersection d’un plan et de la surface. Conceptuellement, la courbure géométrique trouve le cercle le mieux adapté (cercle osculateur) pour s’approcher de la forme de la courbe en tout point. La courbe est la réciproque du rayon de ce cercle (1/r). Une ligne plus droite s’adapte mieux à un cercle plus grand et produit une courbe plus petite, et une ligne courbe plus étroite convient davantage pour un cercle plus petit produisant une courbe plus importante (Crane, 2018).
Courbure (de ligne de pente normale) longitudinale
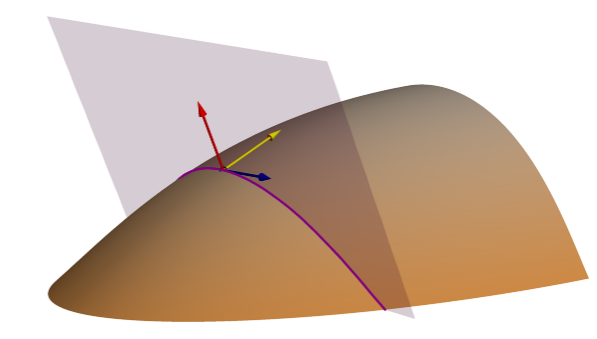
Le paramètre de surface Profile (normal slope line) curvature (Courbure de profil (ligne de pente normale)) mesure la courbure normale géométrique le long de la ligne de pente. Parfois appelée « courbure longitudinale », elle peut être représentée sous la forme d’une section transversale verticale (profil) à travers la surface. Comme illustré ci-dessous, le plan vertical coupe la surface le long de la ligne orange et, s’il était découpé, il apparaîtrait comme une section transversale de la surface.

Ce plan est défini par deux vecteurs : la flèche jaune spécifie la direction de l’inclinaison (flèche de ligne de pente) et la flèche rouge indique la normale à la surface. C’est la combinaison de ces deux vecteurs rouge et jaune qui définit le plan orange et sa ligne d’intersection orange avec la surface. La courbure longitudinale est calculée le long de la ligne orange (ligne de pente normale) dans le plan orange.
La terminologie normale de « ligne de pente normale » de Minár et al (2020) est utilisée ici, afin de réduire le risque d’ambiguïté et de confusion avec la terminologie antérieure.
Cette courbure est généralement appliquée pour caractériser l’accélération et la décélération de l’écoulement sur la surface par la force de gravité. À une vitesse plus élevée, l’eau peut transporter et déplacer des quantités plus importantes de matériaux. Les zones d’accélération deviennent des zones d’érosion et les zones de décélération deviennent des zones de dépôt.
Dans l’image ci-dessous, les zones de courbure longitudinale (ligne de pente normale) fortement convexe au niveau de la crête du cône apparaissent en violet. Les zones de courbure longitudinale (ligne de pente normale) fortement concave à la base du cône sont affichées en orange. Les zones avec de faibles valeurs de courbure sont transparentes.

Les résultats de cette courbure sont différents de ceux de la courbure longitudinale Profile (Profil) obtenue avec l’outil Courbure antérieur. Les différences entre la courbure longitudinale et la courbure longitudinale (ligne de pente) sont expliquées à continuation.
La formule permettant de calculer la courbure longitudinale (ligne de pente normale) est la suivante :
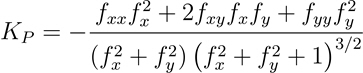
- Où :
KP = courbure longitudinale (ligne de pente normale)
z = f(x,y)
Courbure (d’isoligne normale) tangentielle
Le paramètre de surface Tangential (normal contour) curvature (Courbure tangentielle (isoligne normale)) mesure la courbure normale géométrique perpendiculaire à la ligne de pente, tangente à l’isoligne. Il est appelé courbure tangentielle car il mesure la courbure tangente à l’isoligne. Il est décrit comme une "isoligne normale" (Minár et al., 2020) car le plan de coupe violet qui crée la ligne violette le long de laquelle la courbure est calculée est défini par le vecteur d’isoligne bleu et le vecteur de normale à la surface rouge.
La courbure tangentielle (isoligne normale) est généralement appliquée pour caractériser la convergence et la divergence topographiques de l’écoulement sur la surface.
Dans l’image ci-dessous, les zones de courbure tangentielle (isoligne normale) fortement convexe au niveau de la crête du cône et de la crête en face de vous, apparaissent en bleu. Ce sont des zones où l’écoulement diverge. Les zones de courbure tangentielle (isoligne normale) fortement concave à l’intérieur du cône désignent l’écoulement convergeant en rouge. Les zones avec de faibles valeurs de courbure sont transparentes.

La formule permettant de calculer la courbure tangentielle (isoligne normale) est la suivante :

- Où :
KT = courbure tangentielle (isoligne normale)
z = f(x,y)
Courbure (d’isoligne projetée) transversale
Le paramètre de surface Courbure (d’isoligne projetée) transversale permet de mesurer la courbe le long des isolignes. Elle est parfois appelée « courbure d’isoligne » et « courbure horizontale ». La courbure d’isoligne projetée est mesurée le long de l’isoligne en bleu, à l’intersection du plan horizontal et de la surface.

La formule permettant de calculer la courbure (d’isoligne projetée) transversale est la suivante :

- Où :
KPC = Courbure (d’isoligne projetée) transversale
z = f(x,y)
L’image ci-dessous illustre la différence entre la courbure tangentielle (d’isoligne normale), mesurée le long de la ligne violette, et la courbure (d’isoligne projetée) transversale, mesurée le long de l’isoligne bleue.

Torsion géodésique d’isoligne
Le paramètre de surfarce Torsion géodésique d’isoligne permet de mesurer la vitesse de variation de l’angle de pente le long des isolignes.
La formule de calcul de la tosion géodésique d’isoligne est la suivante :
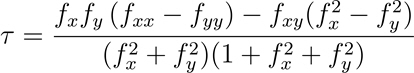
- Où :
τ = Torsion géodésique d’isoligne
z = f(x,y)
Courbure moyenne
Le paramètre de surface Courbure moyenne mesure la courbure globale de la surface. Elle est calculée comme la moyenne de la courbure minimale et la courbure maximale. Il est aussi mathématiquement équivalent à la moyenne des courbures longitudinale (ligne de pente normale) et tangentielle (isoligne normale). Dans l’image ci-dessous, le plan de coupe longitudinal (ligne de pente normale) (orange) et le plan de coupe tangentiel (isoligne normale) (violet) sont représentés.

Les courbures longitudinale (ligne de pente normale) et tangentielle (isoligne normale) mesurent chacune la convexité et la concavité dans une direction spécifique. La courbure moyenne, décrit quant à elle, la convexité ou la concavité intrinsèque de la surface, indépendamment de la direction ou de l’influence de la gravité. Son signe (positif ou négatif) n’est pas un indicateur définitif de la convexité ou de la concavité, excepté aux valeurs extrêmes, puisqu’une surface peut être concave dans une direction et également convexe dans une autre. Les valeurs positives élevées indiquent des zones de dénudation maximale et les valeurs négatives élevées des zones d’accumulation maximale (Minár et al., 2020).
La formule permettant de calculer la courbure moyenne est la suivante :
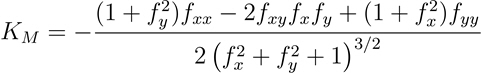
- Où :
KM = courbure moyenne
z = f(x,y)
Courbure gaussienne
Le paramètre de surface Courbure gaussienne mesure la courbure générale d’une surface. Il est calculé comme le produit de la courbure minimale et de la courbure maximale, et peut prendre des valeurs négatives et positives. Des valeurs positives indiquent que la surface est convexe à cette cellule, et des valeurs négatives qu’elle est concave. Une valeur nulle signifie que cette surface est plane.
La formule permettant de calculer la courbure gaussienne est la suivante :

- Où :
KG = Courbure gaussienne
z = f(x,y)
Courbure de Casorati
Le paramètre de surface Courbure de Casorati mesure la courbure générale de la surface. Elle peut être égale à zéro ou à un autre nombre positif quelconque. Des valeurs positives élevées indiquent des zones de pliure nette dans plusieurs directions.
La formule permettant de calculer la courbure de Casorati est la suivante :
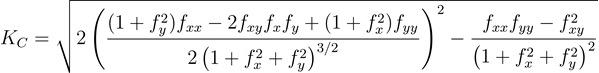
- Où :
KC = Courbure de Casorati
z = f(x,y)
Types de courbures de base et combinatoires
La courbure tangentielle (d’isoligne normale), la courbure (de ligne de pente normale) longitudinale et la torsion géodésique d’isoligne sont considérées comme des types de courbures de base, car les autres courbures peuvent être des combinaisons de celles-ci. En adoptant la terminologie de Minár et al (2020), elles sont décrites comme étant le trio de base.
Outre les expressions indiquées ci-dessus pour la courbure moyenne, la courbure gaussienne et la courbure de Casorati, ces courbures peuvent également être calculées comme étant une combinaison du trio de base.
La formule permettant de calculer la courbure moyenne est la suivante :
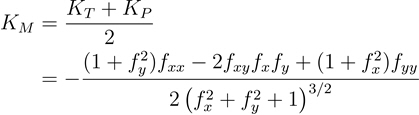
- Où :
KM = courbure moyenne
KT = courbure tangentielle (isoligne normale)
KP = courbure longitudinale (ligne de pente normale)
z = f(x,y)
La formule permettant de calculer la courbure gaussienne est la suivante :

- Où :
KG = Courbure gaussienne
KT = courbure tangentielle (isoligne normale)
KP = courbure longitudinale (ligne de pente normale)
τ = Torsion géodésique d’isoligne
z = f(x,y)
La formule permettant de calculer la courbure de Casorati est la suivante :

- Où :
KC = Courbure de Casorati
KM = courbure moyenne
KG = Courbure gaussienne
z = f(x,y)
Comparaison avec les anciens algorithmes de l'outil Courbure
L’outil Paramètres de surface utilise des algorithmes de courbure différents de ceux de l’outil Courbure, ainsi que des mathématiques géodésiques dans ses calculs. Les résultats de ces deux outils ne sont donc pas directement comparables. Les types de courbures longitudinale (ligne de pente normale) et tangentielle (isoligne normale) de l’outil Paramètres de surface sont des courbures géométriques vraies (Minár et al. 2020). La courbure moyenne de l’outil Paramètres de surface est la moyenne des courbures maximale et minimale à ce point. Les types Profile (Longitudinal) et Planform (Planiforme) de l’outil Courbure sont des dérivées directionnelles, qui ne mesurent pas réellement la courbure géométrique de la surface à un endroit donné (Zevenbergen et Thorne 1987). Le signe (positif ou négatif) de la Courbure longitudinale (ligne de pente normale) de l’outil Paramètres de surface est l’opposé de la Courbure longitudinale de l’outil Courbure. L’outil Paramètres de surface calcule dans l’espace géodésique. L’outil Courbure utilise lui les coordonnées planaires et les mathématiques. L’outil Paramètres de surface peut s’adapter à une surface quadratique ou biquadratique, l’outil Courbure ne prend en charge que les surfaces biquadratiques.
Distance du voisinage
La valeur Distance du voisinage représente la distance sur la carte entre le centre de la cellule de traitement actuelle et le centre d’un voisin orthogonal. Une distance de voisinage plus faible capture une plus grande variabilité locale dans le paysage, qui caractérise les entités de paysage plus petites. Il peut être préférable d’utiliser une distance de voisinage plus grande pour des données d’altitude à résolution plus élevée en raison des erreurs à petite échelle (bruit) dans les données qui ne reflètent pas les processus topographiques d’intérêt, ou parce que la topographie d’intérêt est davantage reconnaissable à de plus grandes échelles.
L’exemple ci-dessous a utilisé un modèle numérique de surface (MNS) d’une résolution de 5 mètres qui comporte un bruit significatif, des artefacts de stries apparaissant dans la courbure longitudinale (ligne de pente normale) finale. La première image a utilisé la fenêtre par défaut de 3 x 3 cellules ou une distance de voisinage de 5 mètres, la deuxième image a utilisé une fenêtre de 9 x 9 cellules ou une distance de voisinage de 20 mètres et la troisième image a fait appel à une fenêtre de 15 x 15 cellules ou une distance de voisinage de 35 mètres. Dans cet exemple, avec l’augmentation de la distance du voisinage, les entités principales ou les plus significatives du paysage sont plus nettes tandis que le bruit et les artefacts sous forme de stries sont moins visibles. Même si une grande distance de voisinage conduit toujours à moins de bruit, la distance la plus adaptée dépend avant tout de la taille de cellule des données et de la taille des entités topographiques qui sont importantes dans le cadre de votre application.
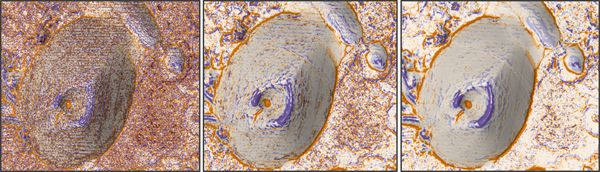
La plus petite distance de voisinage est égale à la taille de cellule du raster en entrée. La plus grande distance de voisinage est égale à sept fois la taille de cellule, ce qui donne une fenêtre de 15 x 15 cellules. Toute distance spécifiée supérieure à sept fois la taille de cellule aura toujours pour résultat une fenêtre de 15 x 15 cellules.

Si la distance de voisinage spécifiée ne produit pas d’intervalle de la taille de cellule ou génère un intervalle de la taille de cellule impair, elle est arrondie à l’intervalle supérieur suivant de la taille de cellule. Par exemple, dans l’illustration ci-dessus, si une distance de voisinage de 25 mètres a été spécifiée, elle est arrondie à l’intervalle supérieur suivant de la taille de cellule, à savoir 30 mètres (trois fois la taille de cellule), ce qui produit une fenêtre de 7 x 7 cellules.
Si les données d’altitude ont une résolution spatiale beaucoup plus fine qu’il n’est nécessaire pour l’analyse des reliefs d’intérêt, une alternative à l’option de la fenêtre de voisinage consiste à rééchantillonner ou à agréger les données selon une taille de cellule plus élevée, qui convient davantage à l’application.
Les calculs des paramètres de surface sont sensibles à la taille de cellule et à la distance du voisinage. Wilson (2018) et Minár et al (2020) ont publié des synthèses efficaces et à jour des nombreuses études sur ce sujet.
Voisinage adaptatif
Lorsqu’il est activé, le paramètre Utiliser le voisinage adaptif modifie la distance de voisinage (taille de fenêtre ou surface) utilisée pour calculer le paramètre de surface, afin de mieux saisir les variations pertinentes du paysage. L’outil détermine automatiquement la taille de fenêtre appropriée en calculant l’écart local par rapport à l’altitude moyenne (DEV) (Wilson and Gallant, 2000) en fonction des valeurs de toutes les cellules du voisinage. L’outil essaie d’utiliser la taille de fenêtre la plus grande possible tout en minimisant la variabilité de la surface (James et al., 2014). La plus grande taille de fenêtre utilisée est spécifiée dans le paramètre Neighborhood distance (Distance de voisinage).
Lorsque le paramètre de surface est calculé avec un voisinage fixe, toutes les valeurs des cellules dans le voisinage sont utilisées. Lorsque le paramètre de surface est calculé avec un voisinage adaptatif, seules neuf cellules (les cellules orthogonales et diagonales extérieures, ainsi que la cellule de traitement du centre) du voisinage sont utilisées.

Le voisinage adaptatif est particulièrement utile pour analyser, à partir d’un MNE haute résolution, un paysage présentant des entités de terrain de taille très variable, telles que des zones très vallonnées avec des petits ruisseaux ou cours d’eau. Dans une telle situation, il est possible d’utiliser une petite distance de voisinage, telle qu’un mètre, pour les ravines des ruisseaux et une distance de voisinage plus importante de 10 ou 15 mètres pour les collines.
Dans l’illustration ci-dessous, un voisinage plus petit est approprié pour le ruisseau et le bord de la falaise, un voisinage plus grand convient pour la transition de la colline à la plaine et un voisinage encore plus grand est adapté au plateau homogène plat à proximité.

Effet de tronçon de la distance du voisinage
Les cellules autour du tronçon externe de la sortie prennent la valeur NoData lorsqu’il n’existe pas suffisamment d’informations disponibles pour le calcul.
Lorsque vous utilisez l’option du voisinage adaptatif, l’étendue du raster en sortie est réduite à son tronçon externe d’une cellule.
Si vous utilisez une distance de voisinage fixe supérieure à la taille de cellule en entrée, l’étendue du raster en sortie. est réduite selon la distance de voisinage utilisée. La réduction peut être calculée comme suit : (largeur de fenêtre en pixels - 1) / 2
Par exemple, si la distance de voisinage génère une fenêtre de 7 x 7 cellules, le raster en sortie est réduit autour de son tronçon externe de trois cellules.
Quadratique et biquadratique
Deux types de surfaces locales peuvent s’adapter à la fenêtre de voisinage : quadratique et biquadratique. Le type par défaut est la surface quadratique qui est recommandée pour la plupart des données et applications.
La surface quadratique est une adaptation selon les moindres carrés des points ; elle ne passe pas exactement par tous les points. Puisqu’elle ne passe pas exactement par tous les points, la surface quadratique a pour effet de minimiser l’impact des données de surface bruyantes (par exemple, une surface lidar haute résolution). Cela permet ainsi d’obtenir des résultats plus représentatifs pour tous les paramètres de surface, ce qui est particulièrement important dans le calcul d’une courbure
La surface quadratique doit être utilisée lorsque vous spécifiez une taille de voisinage supérieure à la taille de cellule et que vous utilisez l’option de voisinage adaptatif.
La surface biquadratique correspond exactement aux données des cellules de voisinage. Cette option convient à une surface en entrée hautement précise, sans bruit aléatoire. Si la distance de voisinage est supérieure à la taille de la cellule raster en entrée, les avantages en termes de précision liés au type de surface biquadratique sont perdus. Il est donc nécessaire de conserver la valeur par défaut (égale à la taille de cellule) de la distance de voisinage.
Transformation de coordonnées géodésiques
L’outil Paramètres de surface effectue ses calculs dans un système de coordonnées 3D géocentriques, également appelé système de coordonnées géocentriques à axes fixes (ECEF), en considérant la forme de la Terre comme un ellipsoïde. Le résultat du calcul n’est pas affecté par la façon dont le jeu de données est projeté. Il utilisera les unités z du raster en entrée s'ils sont définis dans la référence spatiale. Si la référence spatiale de l’entrée ne définit pas les unités z, vous devez le faire avec le paramètre d’unité z.
Le système de coordonnées ECEF est un système de coordonnées cartésien 3D fondé sur la règle de la main droite avec le centre de la terre comme origine, où tout emplacement est représenté par les coordonnées X, Y et Z. La figure ci-dessous donne un exemple d’emplacement cible T exprimé avec des coordonnées géocentriques.
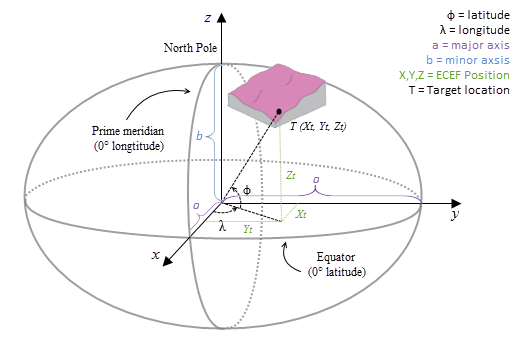
Le raster de surface est transformé du système de coordonnées en entrée en un système de coordonnées 3D géocentriques.
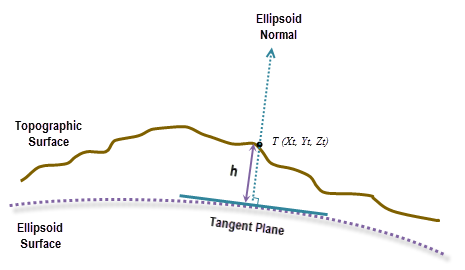
Le calcul géodésique utilise une coordonnée X, Y, Z qui est calculée en fonction de ses coordonnées géodésiques (latitude φ, longitude λ, hauteur h). Si le système de coordonnées du raster de surface en entrée est un système de coordonnées projetées (SCP), le raster est d’abord re-projeté dans un système de coordonnées géographiques (SCG) où chaque emplacement possède une coordonnée géodésique. Il est ensuite transformé en système de coordonnées ECEF. La hauteur h (valeur z) est la hauteur ellipsoïdale sur la surface de l'ellipsoïde. Reportez-vous aux illustrations ci-dessous.
Pour effectuer la transformation en coordonnées ECEF à partir d'une coordonnée géodésique (latitude φ, longitude λ, hauteur h), utilisez les formules suivantes :
X = (N(φ) + h) * cos(φ) * cos(λ)Y = (N(φ) + h) * cos(φ) * sin(λ)Z = (b2 / a2 * N(φ) + h) * sin(φ)- Où :
N(φ) = a2 / √( a2 * cos(φ)2 + b2 * sin(φ)2)φ = latitude
λ = longitude
h = hauteur ellipsoïdale
a = grand axe de l'ellipsoïde
b = petit axe de l’ellipsoïde
La hauteur ellipsoïdale h est en mètres dans les formules ci-dessus. Si l’unité z du raster en entrée est spécifiée dans n’importe quelle autre unité, elle est transformée en mètres.
Lecture recommandée
Pour une meilleure compréhension des méthodes d’analyse de surface et de leurs applications, consultez les références ci-dessous. De plus, Hengl et Reuter (2008), ainsi que Wilson (2018) ont répertorié ces techniques d’analyse de terrain et de nombreuses autres, ainsi que leurs applications. Minár et al (2020) a publié une synthèse complète et claire du travail préalablement effectué sur les courbures de la surface terrestre en les comparant et en définissant de nombreux types de courbures.
Bibliographie
B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice. Section 10.2.1. p. 282.
Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.
Crane K., 2018. Discrete Differential Geometry: An Applied Introduction. Notices of the AMS, Communication. https://www.cs.cmu.edu/~kmcrane/Projects/DDG/paper.pdf
David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.
E.J.Krakiwsky, and D.E.Wells, 1971. Coordinate Systems In Geodesy (GEODESY AND GEOMATICS ENGINEERING, UNB), LECTURE NOTES, No16, 1971, pp. 18-38
Hengl T. and Reuter H. 2008. Geomorphometry Concepts, Software, Applications. Elsevier.
James D.E., M.D. Tomer, S.A. Porter. 2014. Trans-scalar landform segmentation from high-resolution digital elevation models. Affiche présentée à la conférence annuelle des utilisateurs ESRI en juillet 2014 à San Diego, Californie.
Lancaster, P. and Šalkauskas, K. Curve and Surface Fitting: An Introduction. London: Academic Press, 1986.
Marcin Ligas, et Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159
Minár, J., Evans, I. S., & Jenčo, M. (2020). A comprehensive system of definitions of land surface (topographic) curvatures, with implications for their application in geoscience modelling and prediction. Earth-Science Reviews, 103414. https://doi.org/10.1016/j.earscirev.2020.103414
Wilson J.P and Gallant, J.C. (Eds.) 2000. Terrain Analysis: Principles and Applications. John Wiley & Sons, Inc.
Wilson J.P 2018. Environmental Application of Digital Terrain Modeling. John-Blackwell, Inc.
Zevenbergen, L. W., and C. R. Thorne. 1987. Quantitative Analysis of Land Surface Topography. Earth Surface Processes and Landforms 12: 47–56.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?